14.2.2 完全平方公式课件
图片预览






文档简介
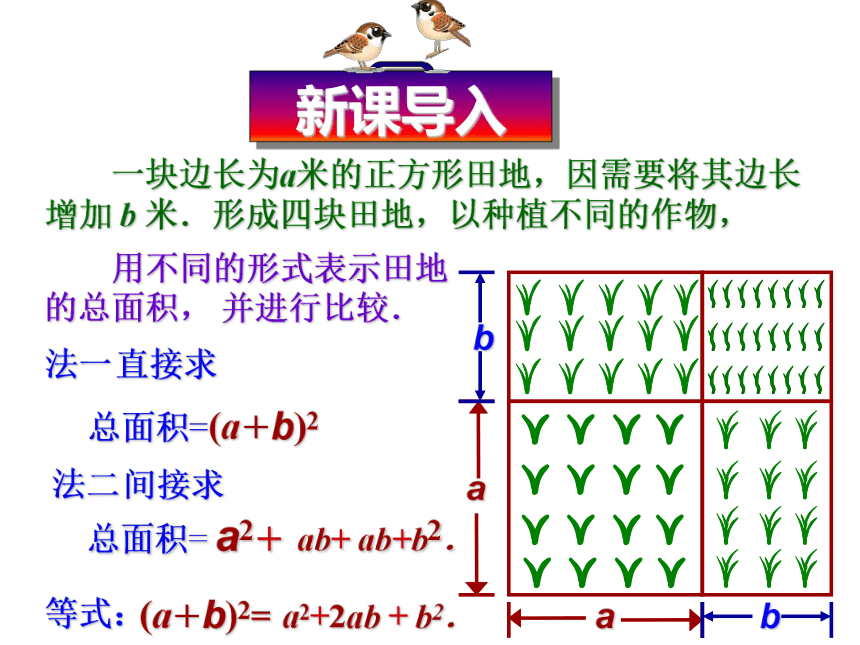
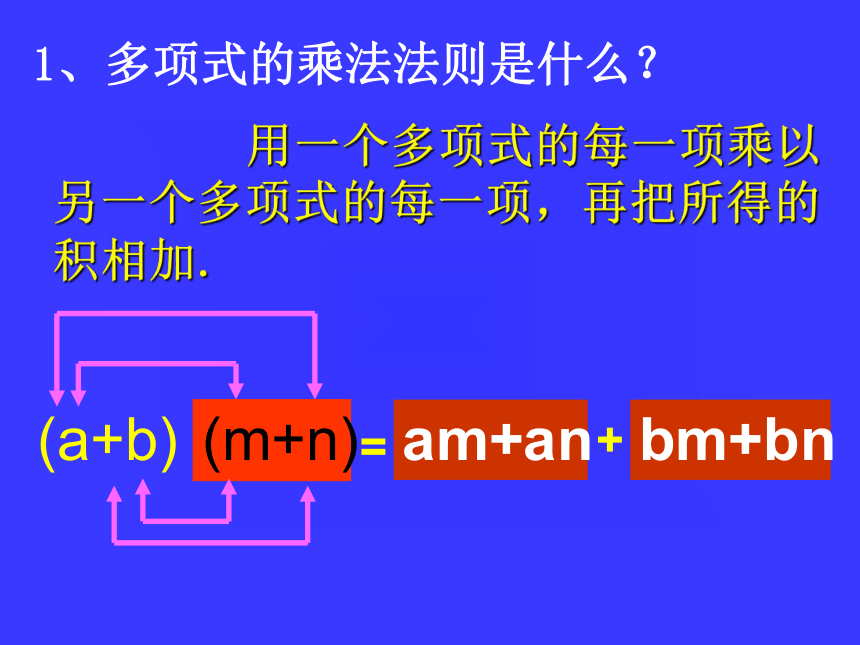
课件33张PPT。 一块边长为a米的正方形田地,因需要将其边长增加 b 米.形成四块田地,以种植不同的作物, 用不同的形式表示田地的总面积, 并进行比较.法一 直接求总面积=(a+b)2 法二间接求总面积= a2+ ab+ ab+b2.(a+b)2= a2+2ab + b2.等式: 用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.1、多项式的乘法法则是什么? am+anbm+bn+=(m+n)(a+b)2、探究
计算下列各式,你能发现什么规律?
(p+1)2 = (p+1) (p+1) = ______
(m+2)2= _________;
(3)(p-1)2 = (p-1 ) (p-1) = ________;
(4) (m-2)2 = __________.P2+2p+1m2+4m+4P2-2p+1m2-4m+4我们来计算(a+b)2, (a-b)2.(a+b)2=(a+b) (a+b)
= a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b)
= a2-ab-ab+b2
=a2-2ab+b2完全平方公式完全平方公式的数学表达式:完全平方公式的文字叙述: 两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍。公式特点:2、积为二次三项式;3、积中两项为两数的平方和;4、另一项是两数积的2倍,且与乘式中间的符号相同;
5 、公式中的字母a,b可以表示数,单项式和多项式。1、左边是一个二项式的完全平方;首平方,尾平方,
乘积的2倍放中央。
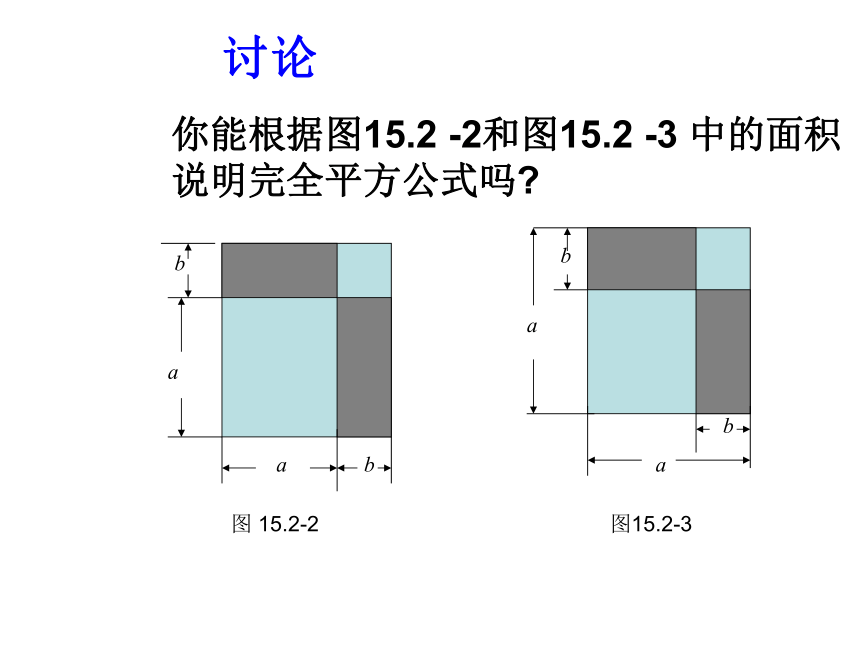
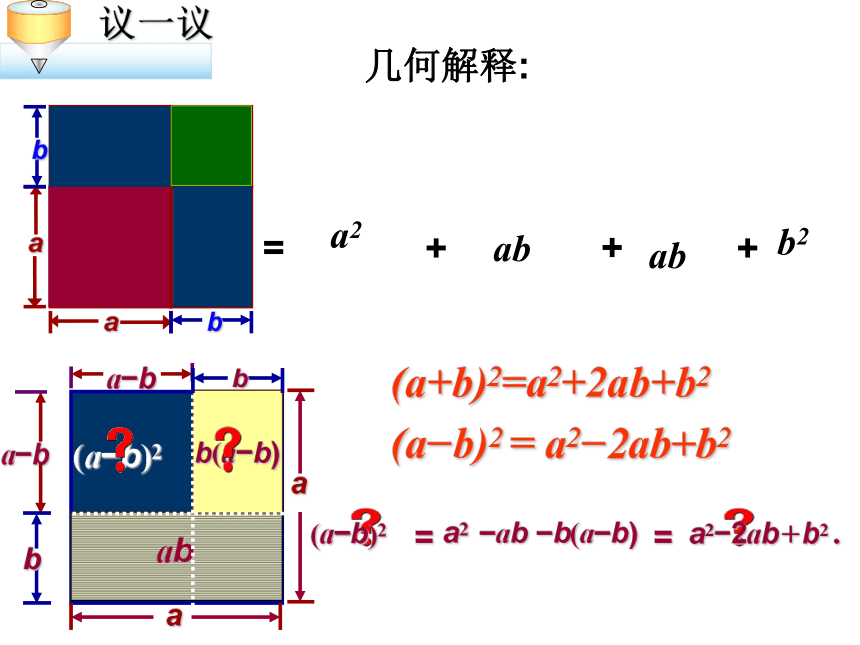
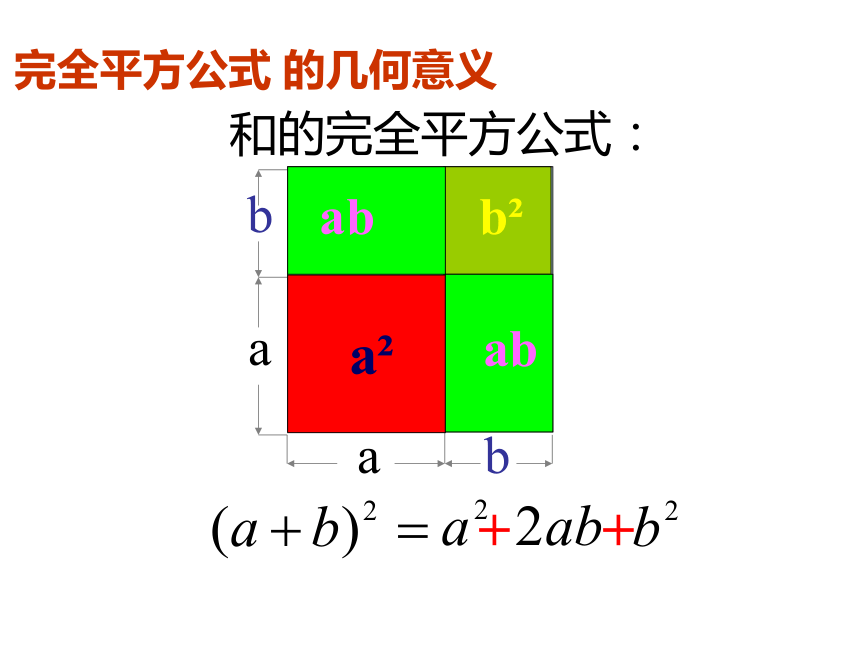
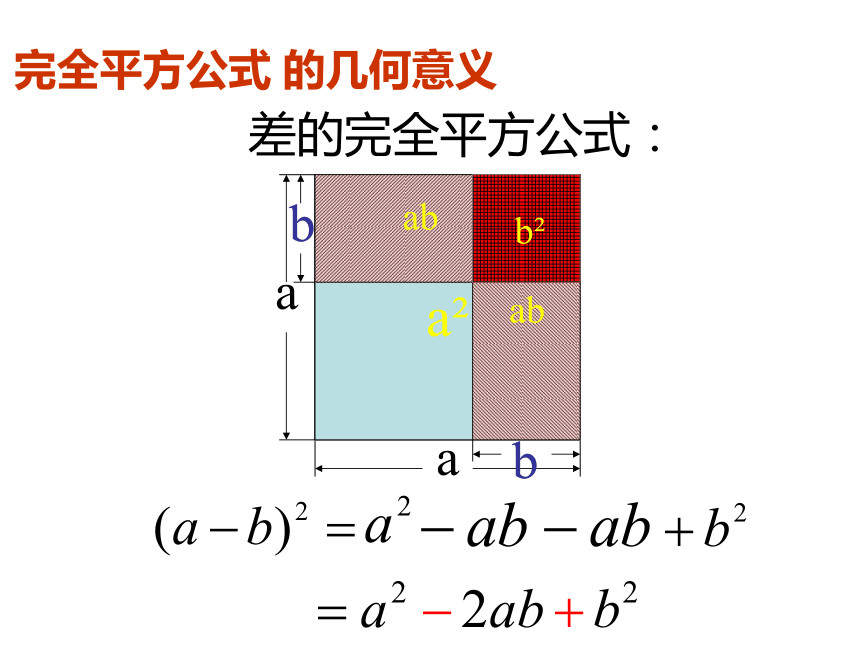
你能根据图15.2 -2和图15.2 -3 中的面积说明完全平方公式吗?讨论=+++(a+b)2=a2+2ab+b2几何解释:a2?ab?b(a?b)=a2?2ab+b2 .=(a?b)2a?ba?bb(a?b)(a?b)2(a?b)2 = a2?2ab+b2
a2ababb2(a+b)2a2b2和的完全平方公式:完全平方公式 的几何意义(a-b)2b2差的完全平方公式:完全平方公式 的几何意义例1、运用完全平方公式计算:解: (4m+n)2==16m2(1)(4m+n)2(a +b)2= a2 + 2 a b + b2(4m)2+2?(4m) ?n+n2+8mn+n2解: (x-2y)2==x2(2)(x-2y)2x2-2?x ?2y+(2y)2-4xy+4y2请 你 找 错 误 指出下列各式中的错误,并加以改正:
(1) (2x?3y)2=2x2 - 2(2x)(3y) +3y2;
(2) (2x+3y)2=4x2+ 9y2 ;
(3) (2x?3y)2=(2x)2- (2x)(3y)+(3y)2. 解 (1)首项、尾项被平方时, 没有添括号,这
样就只把字母平方而遗漏了系数的平方。 (2)少了首项与尾项乘积的2倍这一项 ;即丢
了中间项: 2?(2x)?(3y) ; (3)中间项漏乘了2.比一比 赛一赛 回答下列问题:
(1) (a+2y)2是哪两个数的和的平方?
(a+2y)2 =( ) 2+2( )( )+( ) 2
(2) (2x?5y)2是哪两个数的差的平方?
(2x -5y)2 =( ) 2 -2( )( )+( ) 2aa2y2y2x2x5y5y(2x?5y)2可以看成2x与 ?5y的和的平方.(2x?5y)2可以看成哪两个数的和的平方?
例题解析例题 例2 运用完全平方公式计算:
(1) 1022; (2) 992解: (1) 1022 =(2) 992==1002+2×100×2+22=10000+400+4=10404(100-1)2=1002-2×100×1+12=10000-200+1=98012、准确代入公式;利用完全平方公式计算:1、先选择公式;3、化简. 想一想:
(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
为什么?∵ (a+b)2=a2+2ab+b2(-a-b)2=(-a)2+2(-a)(-b)+(-b) 2=a2+2ab+b2∵ (a-b)2=a2-2ab+b2 (b-a)2=b2-2ba+a2=a2-2ab+b2∴ (a+b)2= (-a-b)2∴ (a-b)2=(b-a)2xx 662a2a3b3bx2+12x+364a2-12ab+9b2+(-6)2=x2+12x+36+(2a)2=9b2-12ab+4a2通过观察发现:(x+6)2=(-x-6)2 (2a-3b)2 =(3b-2a)2
相等相等(-x)2 -2(-x)(6)(3b)2-2(3b)(2a)练习
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
2.下面各式的计算错在哪里?应当怎样改正?
(1) (a+ b)2 = a2 +b2;
(2) (a – b) 2 =a2 – b2.
(3)例3.若
求
拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2(1) (3a+__ )2=9a2- ___ +16(2)代数式2xy-x2-y2= ( )
A.(x-y)2 B.(-x-y)2
C.(y-x)2 D.-(x-y)2
D拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2(3)如果x2+kx+25是完全平方式,
则 k=_____.
±5±24拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b240(5)已知 a+b = 4,ab = -12,
则a2 + b2= .(6)已知 m+n= 3,mn = 5,
求:(m+3)(n+3)的值.拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2通过这节课的学习你学到了什么小结:(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、完全平方公式: 2 、两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍。3、注意:项数、符号、字母及其指数; 下列等式是否成立? 说明理由.
(?4a+1)2=(1?4a)2;
(2) (?4a?1)2=(4a+1)2;
(3) (4a?1)(1?4a)=(4a?1)(4a?1)=(4a?1)2;
(4) (4a?1)(?1?4a)=(4a?1)(4a+1).成立成立不成立.不成立.试一试:填空题:
(1)(-3x+4y)2=_____________.
(2)(-2a-b)2=____________.
(3)x2-4xy+________=(x-2y)2.
(4)a2+b2=(a+b)2+_________.
(5) a2+______+9b2=( a+3b)2综合训练:9x2-24xy+16y2 4a2+4ab+b2 4y2 (-2ab) 3ab 选择题
(1)如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(2)将正方形的边长由acm增加6cm,则正方形的面积增加了( )
A.36cm2 B.12acm2
C.(36+12a)cm2 D.以上都不对你会吗?cc1. =_______;
2.若 是一个完全平方公式,
则 _______;
3.若 是一个完全平方公式,
则 _______;1拓展: 4.请添加一项________,使得 是
完全平方式.5.思考题:已知:
求: 和 的值拓展:拓展延伸若
计算下列各式,你能发现什么规律?
(p+1)2 = (p+1) (p+1) = ______
(m+2)2= _________;
(3)(p-1)2 = (p-1 ) (p-1) = ________;
(4) (m-2)2 = __________.P2+2p+1m2+4m+4P2-2p+1m2-4m+4我们来计算(a+b)2, (a-b)2.(a+b)2=(a+b) (a+b)
= a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b)
= a2-ab-ab+b2
=a2-2ab+b2完全平方公式完全平方公式的数学表达式:完全平方公式的文字叙述: 两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍。公式特点:2、积为二次三项式;3、积中两项为两数的平方和;4、另一项是两数积的2倍,且与乘式中间的符号相同;
5 、公式中的字母a,b可以表示数,单项式和多项式。1、左边是一个二项式的完全平方;首平方,尾平方,
乘积的2倍放中央。
你能根据图15.2 -2和图15.2 -3 中的面积说明完全平方公式吗?讨论=+++(a+b)2=a2+2ab+b2几何解释:a2?ab?b(a?b)=a2?2ab+b2 .=(a?b)2a?ba?bb(a?b)(a?b)2(a?b)2 = a2?2ab+b2
a2ababb2(a+b)2a2b2和的完全平方公式:完全平方公式 的几何意义(a-b)2b2差的完全平方公式:完全平方公式 的几何意义例1、运用完全平方公式计算:解: (4m+n)2==16m2(1)(4m+n)2(a +b)2= a2 + 2 a b + b2(4m)2+2?(4m) ?n+n2+8mn+n2解: (x-2y)2==x2(2)(x-2y)2x2-2?x ?2y+(2y)2-4xy+4y2请 你 找 错 误 指出下列各式中的错误,并加以改正:
(1) (2x?3y)2=2x2 - 2(2x)(3y) +3y2;
(2) (2x+3y)2=4x2+ 9y2 ;
(3) (2x?3y)2=(2x)2- (2x)(3y)+(3y)2. 解 (1)首项、尾项被平方时, 没有添括号,这
样就只把字母平方而遗漏了系数的平方。 (2)少了首项与尾项乘积的2倍这一项 ;即丢
了中间项: 2?(2x)?(3y) ; (3)中间项漏乘了2.比一比 赛一赛 回答下列问题:
(1) (a+2y)2是哪两个数的和的平方?
(a+2y)2 =( ) 2+2( )( )+( ) 2
(2) (2x?5y)2是哪两个数的差的平方?
(2x -5y)2 =( ) 2 -2( )( )+( ) 2aa2y2y2x2x5y5y(2x?5y)2可以看成2x与 ?5y的和的平方.(2x?5y)2可以看成哪两个数的和的平方?
例题解析例题 例2 运用完全平方公式计算:
(1) 1022; (2) 992解: (1) 1022 =(2) 992==1002+2×100×2+22=10000+400+4=10404(100-1)2=1002-2×100×1+12=10000-200+1=98012、准确代入公式;利用完全平方公式计算:1、先选择公式;3、化简. 想一想:
(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
为什么?∵ (a+b)2=a2+2ab+b2(-a-b)2=(-a)2+2(-a)(-b)+(-b) 2=a2+2ab+b2∵ (a-b)2=a2-2ab+b2 (b-a)2=b2-2ba+a2=a2-2ab+b2∴ (a+b)2= (-a-b)2∴ (a-b)2=(b-a)2xx 662a2a3b3bx2+12x+364a2-12ab+9b2+(-6)2=x2+12x+36+(2a)2=9b2-12ab+4a2通过观察发现:(x+6)2=(-x-6)2 (2a-3b)2 =(3b-2a)2
相等相等(-x)2 -2(-x)(6)(3b)2-2(3b)(2a)练习
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
2.下面各式的计算错在哪里?应当怎样改正?
(1) (a+ b)2 = a2 +b2;
(2) (a – b) 2 =a2 – b2.
(3)例3.若
求
拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2(1) (3a+__ )2=9a2- ___ +16(2)代数式2xy-x2-y2= ( )
A.(x-y)2 B.(-x-y)2
C.(y-x)2 D.-(x-y)2
D拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2(3)如果x2+kx+25是完全平方式,
则 k=_____.
±5±24拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b240(5)已知 a+b = 4,ab = -12,
则a2 + b2= .(6)已知 m+n= 3,mn = 5,
求:(m+3)(n+3)的值.拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2拓展思维 更上一层(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2通过这节课的学习你学到了什么小结:(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、完全平方公式: 2 、两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍。3、注意:项数、符号、字母及其指数; 下列等式是否成立? 说明理由.
(?4a+1)2=(1?4a)2;
(2) (?4a?1)2=(4a+1)2;
(3) (4a?1)(1?4a)=(4a?1)(4a?1)=(4a?1)2;
(4) (4a?1)(?1?4a)=(4a?1)(4a+1).成立成立不成立.不成立.试一试:填空题:
(1)(-3x+4y)2=_____________.
(2)(-2a-b)2=____________.
(3)x2-4xy+________=(x-2y)2.
(4)a2+b2=(a+b)2+_________.
(5) a2+______+9b2=( a+3b)2综合训练:9x2-24xy+16y2 4a2+4ab+b2 4y2 (-2ab) 3ab 选择题
(1)如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(2)将正方形的边长由acm增加6cm,则正方形的面积增加了( )
A.36cm2 B.12acm2
C.(36+12a)cm2 D.以上都不对你会吗?cc1. =_______;
2.若 是一个完全平方公式,
则 _______;
3.若 是一个完全平方公式,
则 _______;1拓展: 4.请添加一项________,使得 是
完全平方式.5.思考题:已知:
求: 和 的值拓展:拓展延伸若
