江苏省盐城市阜宁县2017-2018学年高一上学期期中考试数学试题
文档属性
| 名称 | 江苏省盐城市阜宁县2017-2018学年高一上学期期中考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-27 00:00:00 | ||
图片预览



文档简介
高一年级期中检测
数学试卷
一、填空题:(14×5分=70分)
1.已知集合集合,则 .
2. 若,则符合条件的集合有 个.
3. 已知函数满足,则= .
4.幂函数,其中。若为偶函数,则的取值集合为 .
5.函数的定义域为 .
6. 设,,若,则实数的取值范围是 .
7.已知函数的零点在区间内,则整数= .
8.函数的单调减区间为 .
9.若则 .
10.函数在不是单调函数,则的取值范围
11. 若函数的最大值为,且f(x)是偶函数,则=________.
12. 已知函数满足当时总有,
若,则实数的取值范围是 .
13. 已知函数是定义在R上的奇函数,且对任意满足,又当时,,则 .14.已知函数,函数,其中,若函数恰有4个零点,则的取值范围为 .
二、解答题:(14′+14′+14′+16′+16′+16′=90′)
15.设全集为,或,.
求(1);
(2)()
16(1)求值: ;
(2)解不等式(且).
17.已知函数是定义在上的奇函数,且当时,.
(1)求函数的解析式;
(2)若,求实数的取值范围。
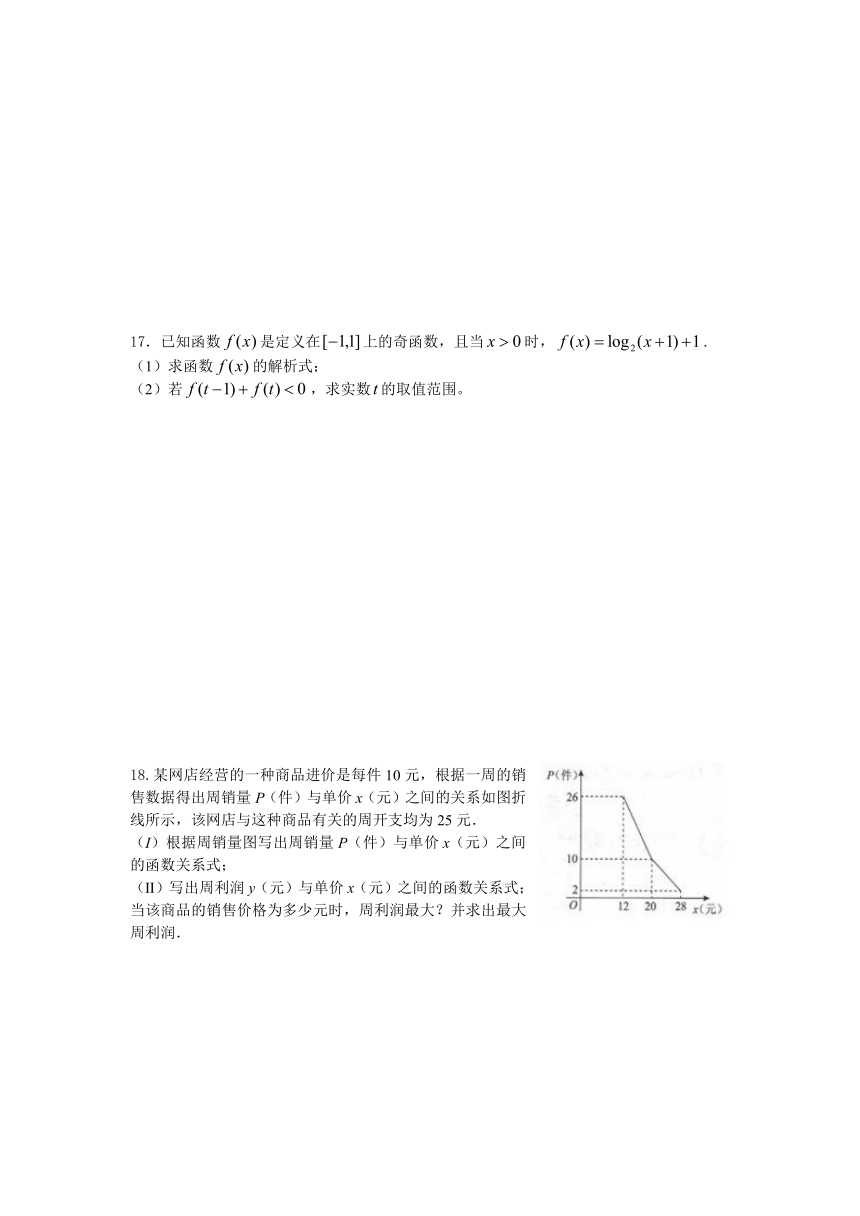
18.某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元. (I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式; (Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
19.已知函数,
判断函数的奇偶性并证明;
当,求函数的最小值;
(3)如果不等式对于任意恒成立,求实数的取值范围.
20.已知关于x的函数f(x)=x2-2ax+2. (1)当a≤2时,求f(x)在[,3]上的最小值g(a); (2)如果函数f(x)同时满足: ①函数在整个定义域上是单调增函数或单调减函数; ②在函数的定义域内存在区间 [p,q],使得函数在区间[p,q]上的值域为[p2,q2].则我们称函数f(x)是该定义域上的“闭函数”. (i)若关于x的函数y=+t(x≥1)是“闭函数”,求实数t的取值范围; (ii)判断(1)中g(a)是否为“闭函数”?若是,求出p,q的值或关系式;若不是,请说明理由.
; 2. 8; 3.; 4 .; 5.;
; 7. 1; 8. ; 9 . 26; 10. 11 . 1 ; 12.; 13.-2; 14.
(1).................7分
(2) ()=.................14分
(1).................6分
当时解集为;.................10分
当时解集为.................14分
解:(I)当x∈[12,20]时,P=k1x+b1,代入点(12,26),(20,10)得k1=-2,b1=50,∴P=-2x+50; 同理x∈(20,28]时,P=-x+30, ∴周销量P(件)与单价x(元)之间的函数关系式P=; (Ⅱ)y=P(x-10)-25=, 当x∈[12,20]时,y=,x=时,ymax=; x∈(20,28]时,y=-(x-20)2+75,函数单调递减,∴y<75, 综上所述,x=时,ymax=.
(3)
20. 解:(1)函数f(x)=x2-2ax+2=(x-a)2+2-a2,其对称轴方程为x=a, 当a≤时,f(x)在[,3]上单调递增,其最小值为g(a)=f()=-; 当≤a≤2时,f(x)在[,3]上的最小值为g(a)=f(a)=2-a2; 函数f(x)=x2-2ax+2在[,3]上的最小值g(a)= (2)(i)∵y=+t在[1,+∞)递增, 由闭函数的定义知,该函数在定义域[1,+∞)内, 存在区间[p,q](p<q),使得该函数在区间[p,q]上的值域为[p2,q2],所以p≥1,, ∴p2,q2为方程+t=x的二实根, 即方程x2-(2t+1)x+t2+1=0在[1,+∞)上存在两个不等的实根且x≥t恒成立, 令u(x)=x2-(2t+1)x+t2+1, ∴,∴, 解得<t≤1 ∴实数t的取值范围(,1]. (ii)对于(1),易知g(a)在(-∞,2]上为减函数, ①若p<q≤,g(a)递减,若g(a)为“闭函数”, 则, 两式相减得p+q=,这与p<q≤矛盾. ②<p<q≤2时,若g(a)为“闭函数”,则 此时p2+q2=2满足条件的p,q存在, ∴<p<q≤2时,使得g(a)为“闭函数”p,q存在, ③p≤<q≤2时,若g(a)为“闭函数”,则, 消去q得9p2-6p+1=0,即(3p-1)2=0 解得p=此时,q=<2,且p2+q2=2 ∴p=<q≤2时,使得g(a)为“闭函数”p,q存在, 综上所述,当p,q满足时,g(a)为“闭函数”
数学试卷
一、填空题:(14×5分=70分)
1.已知集合集合,则 .
2. 若,则符合条件的集合有 个.
3. 已知函数满足,则= .
4.幂函数,其中。若为偶函数,则的取值集合为 .
5.函数的定义域为 .
6. 设,,若,则实数的取值范围是 .
7.已知函数的零点在区间内,则整数= .
8.函数的单调减区间为 .
9.若则 .
10.函数在不是单调函数,则的取值范围
11. 若函数的最大值为,且f(x)是偶函数,则=________.
12. 已知函数满足当时总有,
若,则实数的取值范围是 .
13. 已知函数是定义在R上的奇函数,且对任意满足,又当时,,则 .14.已知函数,函数,其中,若函数恰有4个零点,则的取值范围为 .
二、解答题:(14′+14′+14′+16′+16′+16′=90′)
15.设全集为,或,.
求(1);
(2)()
16(1)求值: ;
(2)解不等式(且).
17.已知函数是定义在上的奇函数,且当时,.
(1)求函数的解析式;
(2)若,求实数的取值范围。
18.某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元. (I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式; (Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
19.已知函数,
判断函数的奇偶性并证明;
当,求函数的最小值;
(3)如果不等式对于任意恒成立,求实数的取值范围.
20.已知关于x的函数f(x)=x2-2ax+2. (1)当a≤2时,求f(x)在[,3]上的最小值g(a); (2)如果函数f(x)同时满足: ①函数在整个定义域上是单调增函数或单调减函数; ②在函数的定义域内存在区间 [p,q],使得函数在区间[p,q]上的值域为[p2,q2].则我们称函数f(x)是该定义域上的“闭函数”. (i)若关于x的函数y=+t(x≥1)是“闭函数”,求实数t的取值范围; (ii)判断(1)中g(a)是否为“闭函数”?若是,求出p,q的值或关系式;若不是,请说明理由.
; 2. 8; 3.; 4 .; 5.;
; 7. 1; 8. ; 9 . 26; 10. 11 . 1 ; 12.; 13.-2; 14.
(1).................7分
(2) ()=.................14分
(1).................6分
当时解集为;.................10分
当时解集为.................14分
解:(I)当x∈[12,20]时,P=k1x+b1,代入点(12,26),(20,10)得k1=-2,b1=50,∴P=-2x+50; 同理x∈(20,28]时,P=-x+30, ∴周销量P(件)与单价x(元)之间的函数关系式P=; (Ⅱ)y=P(x-10)-25=, 当x∈[12,20]时,y=,x=时,ymax=; x∈(20,28]时,y=-(x-20)2+75,函数单调递减,∴y<75, 综上所述,x=时,ymax=.
(3)
20. 解:(1)函数f(x)=x2-2ax+2=(x-a)2+2-a2,其对称轴方程为x=a, 当a≤时,f(x)在[,3]上单调递增,其最小值为g(a)=f()=-; 当≤a≤2时,f(x)在[,3]上的最小值为g(a)=f(a)=2-a2; 函数f(x)=x2-2ax+2在[,3]上的最小值g(a)= (2)(i)∵y=+t在[1,+∞)递增, 由闭函数的定义知,该函数在定义域[1,+∞)内, 存在区间[p,q](p<q),使得该函数在区间[p,q]上的值域为[p2,q2],所以p≥1,, ∴p2,q2为方程+t=x的二实根, 即方程x2-(2t+1)x+t2+1=0在[1,+∞)上存在两个不等的实根且x≥t恒成立, 令u(x)=x2-(2t+1)x+t2+1, ∴,∴, 解得<t≤1 ∴实数t的取值范围(,1]. (ii)对于(1),易知g(a)在(-∞,2]上为减函数, ①若p<q≤,g(a)递减,若g(a)为“闭函数”, 则, 两式相减得p+q=,这与p<q≤矛盾. ②<p<q≤2时,若g(a)为“闭函数”,则 此时p2+q2=2满足条件的p,q存在, ∴<p<q≤2时,使得g(a)为“闭函数”p,q存在, ③p≤<q≤2时,若g(a)为“闭函数”,则, 消去q得9p2-6p+1=0,即(3p-1)2=0 解得p=此时,q=<2,且p2+q2=2 ∴p=<q≤2时,使得g(a)为“闭函数”p,q存在, 综上所述,当p,q满足时,g(a)为“闭函数”
同课章节目录
