第3章 投影与视图单元检测A卷
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
投影与视图单元检测A卷
姓名:__________班级:__________学号:__________
一.选择题(共9小题)
1.正方形的正投影不可能是( )
A.线段 B.矩形 C.正方形 D.梯形
2.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
A.0.324πm2 B.0.288πm2 C.1.08πm2 D.0.72πm2
3.如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )21cnjy.com
A.E处 B.F处 C.G处 D.H处
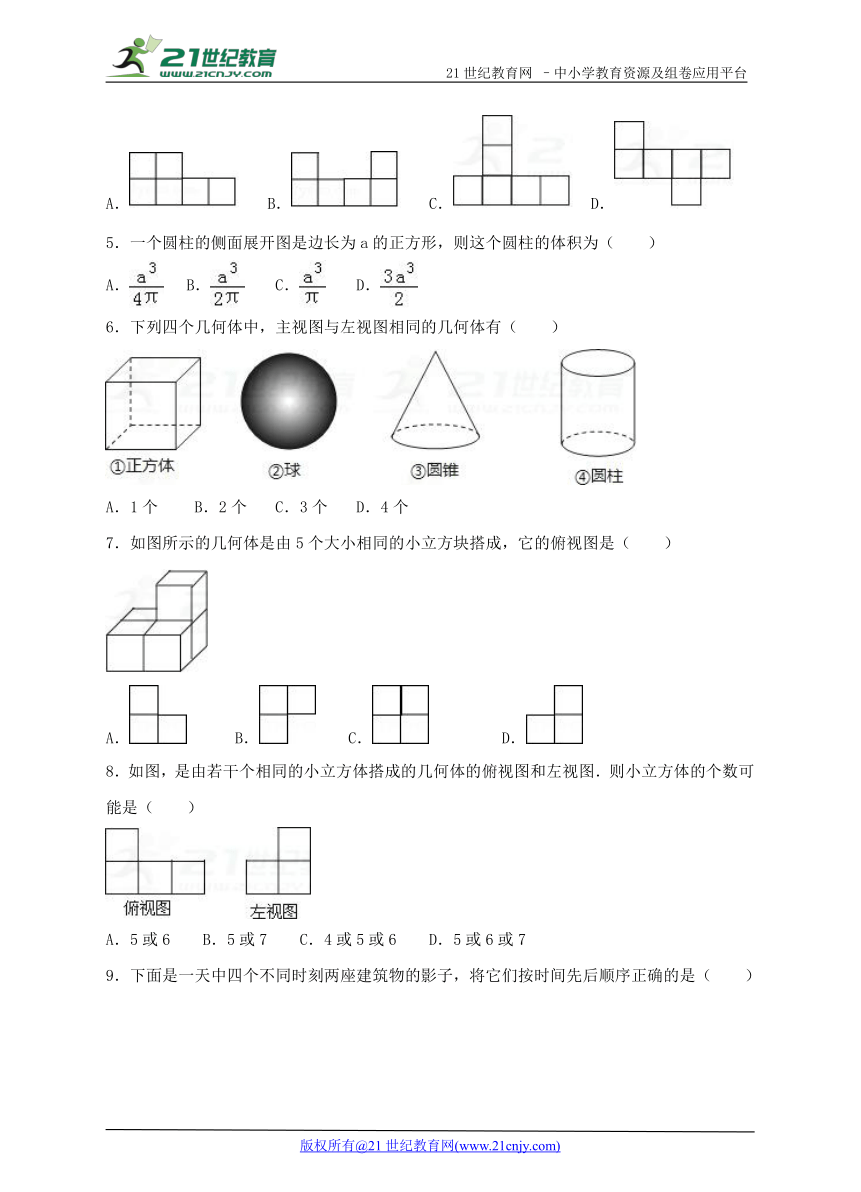
4.下列图形中,可以是正方体表面展开图的是( )
A. B. C. D.
5.一个圆柱的侧面展开图是边长为a的正方形,则这个圆柱的体积为( )
A. B. C. D.
6.下列四个几何体中,主视图与左视图相同的几何体有( )
A.1个 B.2个 C.3个 D.4个
7.如图所示的几何体是由5个大小相同的小立方块搭成,它的俯视图是( )
A. B. C. D.
8.如图,是由若干个相同的小立方体搭成的几何体的俯视图和左视图.则小立方体的个数可能是( )
A.5或6 B.5或7 C.4或5或6 D.5或6或7
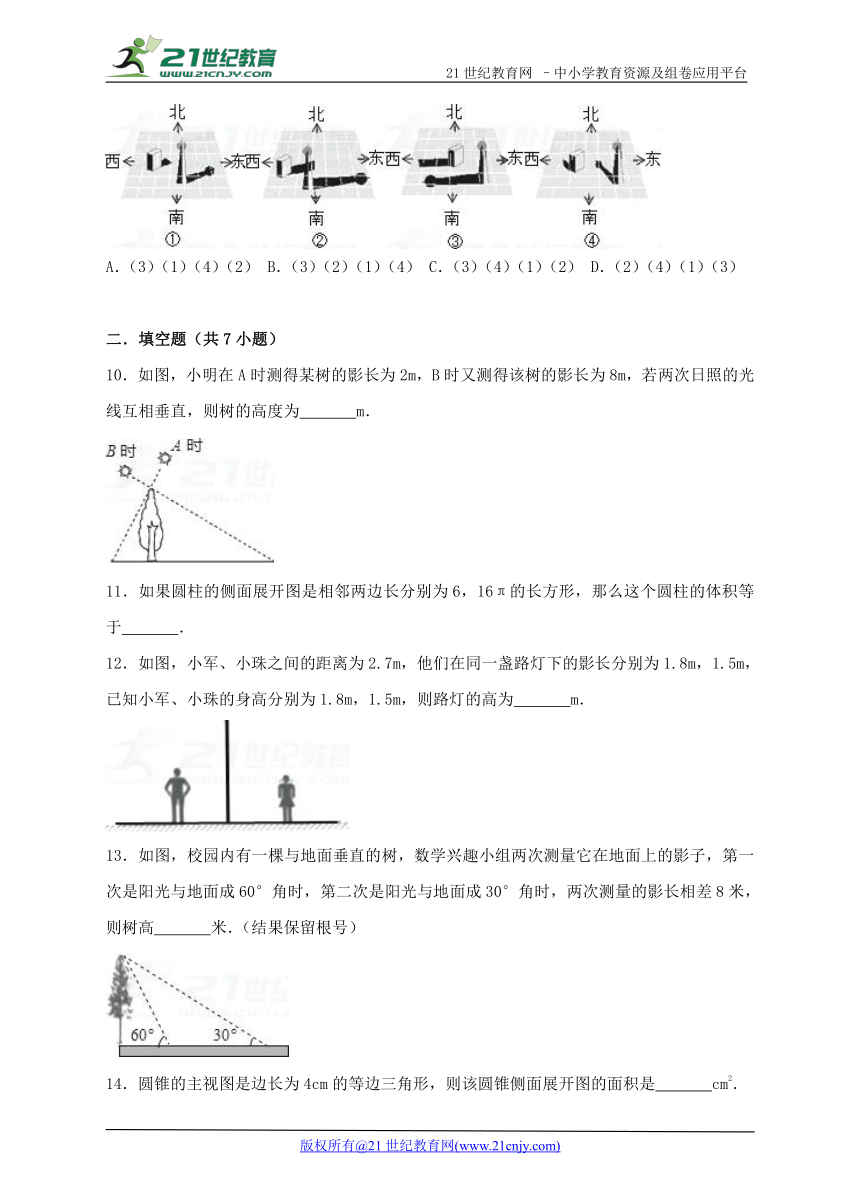
9.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是( )
A.(3)(1)(4)(2) B.(3)(2)(1)(4) C.(3)(4)(1)(2) D.(2)(4)(1)(3)
二.填空题(共7小题)
10.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为 m.2·1·c·n·j·y
11.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
12.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为 m.
13.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高 米.(结果保留根号)【来源:21·世纪·教育·网】
14.圆锥的主视图是边长为4cm的等边三角形,则该圆锥侧面展开图的面积是 cm2.
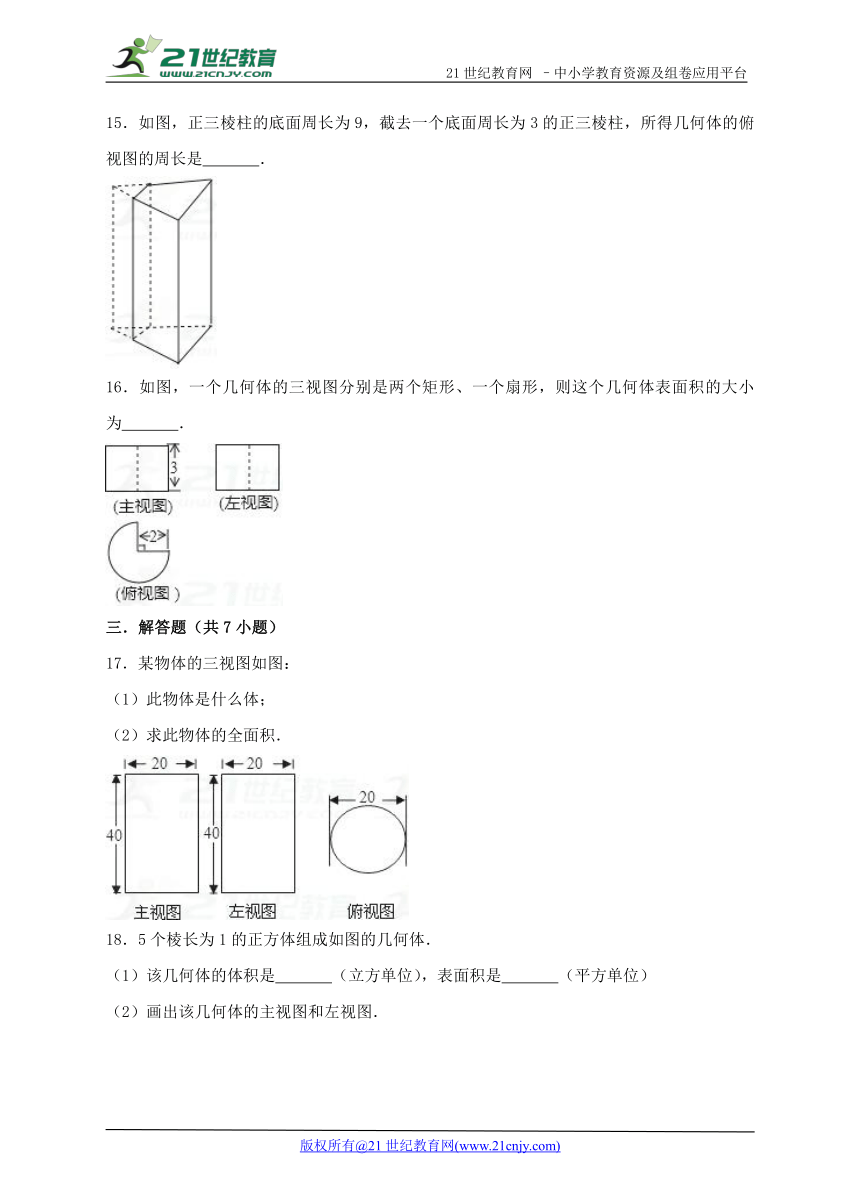
15.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .www-2-1-cnjy-com
16.如图,一个几何体的三视图分别是两个矩形、一个扇形,则这个几何体表面积的大小为 .
三.解答题(共7小题)
17.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
18.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 (立方单位),表面积是 (平方单位)
(2)画出该几何体的主视图和左视图.
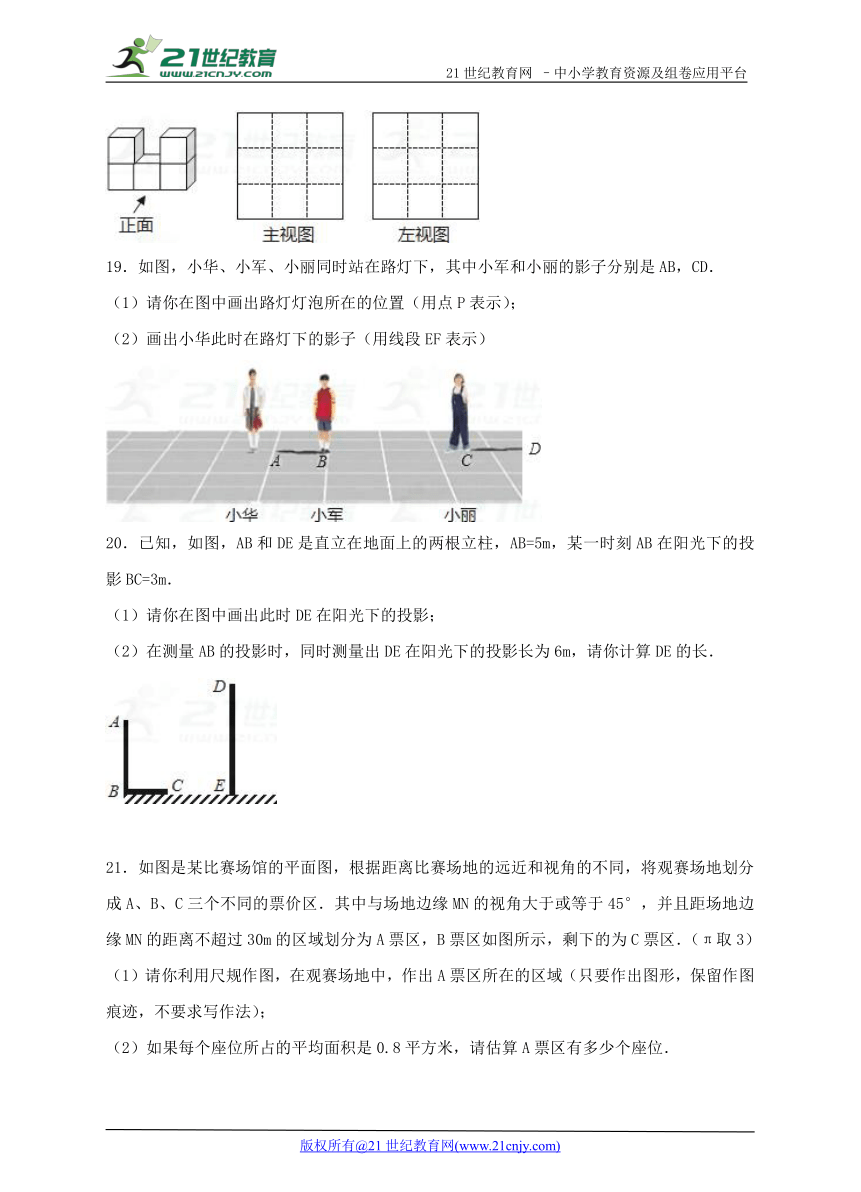
19.如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD.
(1)请你在图中画出路灯灯泡所在的位置(用点P表示);
(2)画出小华此时在路灯下的影子(用线段EF表示)
20.已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.21*cnjy*com
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
21.如图是某比赛场馆的平面图,根据距离比赛场地的远近和视角的不同,将观赛场地划分成A、B、C三个不同的票价区.其中与场地边缘MN的视角大于或等于45°,并且距场地边缘MN的距离不超过30m的区域划分为A票区,B票区如图所示,剩下的为C票区.(π取3)
(1)请你利用尺规作图,在观赛场地中,作出A票区所在的区域(只要作出图形,保留作图痕迹,不要求写作法);【来源:21cnj*y.co*m】
(2)如果每个座位所占的平均面积是0.8平方米,请估算A票区有多少个座位.
22.如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示.已知展开图中每个正方形的边长为1.21教育名师原创作品
(1)求在该展开图中可画出最长线段的长度这样的线段可画几条?
(2)试比较立体图中∠BAC与平面展开图中∠B′A′C′的大小关系?
23.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
答案与解析
一.选择题(共9小题)
1.【分析】根据平行投影的特点:在同一时刻,平行物体的投影仍旧平行,即可得出答案.
解:在同一时刻,平行物体的投影仍旧平行.得到的应是平行四边形或特殊的平行四边形或线段.
故正方形纸板ABCD的正投影不可能是梯形,
故选:D.
2.【分析】先根据AC⊥OB,BD⊥OB可得出△AOC∽△BOD,由相似三角形的对应边成比例可求出BD的长,进而得出BD′=0.3m,再由圆环的面积公式即可得出结论.
解:如图所示:∵AC⊥OB,BD⊥OB,
∴△AOC∽△BOD,
∴=,即=,
解得:BD=0.9m,
同理可得:AC′=0.2m,则BD′=0.3m,
∴S圆环形阴影=0.92 π﹣0.32π=0.72π(m2).
故选:D.
3.【分析】根据各选项安装位置判断能否覆盖所有空白部分即可.
解:如图,
A、若安装在E处,仍有区域:四边形MGNS和△PFI监控不到,此选项错误;
B、若安装在F处,仍有区域:△ERW监控不到,此选项错误;
C、若安装在G处,仍有区域:四边形QEWK监控不到,此选项错误;
D、若安装在H处,所有空白区域均能监控,此选项正确;
故选:D.
4.【分析】观察选项中的图形,确定出作为正方体表面展开图的即可.
解:下列图形中,可以是正方体表面展开图的是,
故选D
5.【分析】根据圆柱的侧面展开图确定出圆柱的底面半径与高,即可求出其体积.
解:根据题意得:()2π×a=,
故选A
6.【分析】主视图、左视图是分别从物体正面、左面看,所得到的图形.分别分析四种几何体的主视图与左视图,即可求解.21教育网
解:①正方体的主视图与左视图都是正方形;
②球的主视图与左视图都是圆;
③圆锥主视图与左视图都是三角形;
④圆柱的主视图和左视图都是长方形;
故选:D.
7.【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
解:从上面看易得横着的“”字,
故选C.
8.【分析】易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由左视图可得第二层最多和最少小立方体的个数,相加即可.www.21-cn-jy.com
解:由俯视图易得最底层有4个小立方体,由左视图易得第二层最多有3个小立方体和最少有1个小立方体,
那么小立方体的个数可能是5个或6个或7个.
故选D.
9.【分析】根据从早晨到傍晚物体影子的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.
解:西为(3),西北为(4),东北为(1),东为(2),
∴将它们按时间先后顺序排列为(3)(4)(1)(2).
故选:C.
二.填空题(共7小题)
10.【分析】根据题意,画出示意图,易得:Rt△EDC∽Rt△CDF,进而可得=;即DC2=ED FD,代入数据可得答案.
解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED FD,
代入数据可得DC2=16,
DC=4;
故答案为:4.
11.【分析】分两种情况:①底面周长为6高为16π;②底面周长为16π高为6;先根据底面周长得到底面半径,再根据圆柱的体积公式计算即可求解.
解:①底面周长为6高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
12.【分析】根据CD∥AB∥MN,得到△ABE∽△CDE,△ABF∽△MNF,根据相似三角形的性质可知,,即可得到结论.21·cn·jy·com
解:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴,,
即,,
解得:AB=3m.
答:路灯的高为3m.
13.【分析】设出树高,利用所给角的正切值分别表示出两次影子的长,然后作差建立方程即可.
解:如图,
在RtABC中,tan∠ACB=,
∴BC==,
同理:BD=,
∵两次测量的影长相差8米,
∴﹣=8,
∴x=4
故答案为4.
14.【分析】根据题意确定出圆锥的底面半径与母线,进而确定出侧面展开图面积即可.
解:根据题意得:圆锥的底面半径为2cm,母线长为4cm,
则该圆锥侧面展开图的面积是8πcm2.
故答案为:8π
15.【分析】根据从上边看得到的图形是俯视图,可得答案.
解:从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为:8.
16.【分析】由几何体的三视图得出该几何体的表面是由3个长方形与两个扇形围成,结合图中数据求出组合体的表面积即可.21世纪教育网版权所有
解:由几何体的三视图可得:
该几何体的表面是由3个长方形与两个扇形围成,
该几何体的表面积为:S=2×2×3+×2+×3=12+15π,
故答案为:12+15π.
三.解答题(共7小题)
17.【分析】考查立体图形的三视图,圆柱的全面积的求法及公式的应用.
解:(1)根据三视图的知识,主视图以及左视图都为矩形,俯视图是一个圆,故可判断出该几何体为圆柱.(2分)21·世纪*教育网
(2)根据圆柱的全面积公式可得,20π×40+2×π×102=1000π(6分).
18.【分析】(1)几何体的体积为5个正方体的体积和,表面积为20个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形(外面4个加里面2个),每个正方形的面积为1,【出处:21教育名师】
∴组合几何体的表面积为22.
故答案为:5,22;
(2)作图如下:
19.【分析】(1)根据小军和小丽的身高与影长即可得到光源所在;
(2)根据光源所在和小华的身高即可得到相应的影长.
解:如图所示:
(1)点P就是所求的点;
(2)EF就是小华此时在路灯下的影子.
20.【分析】(1)根据投影的定义,作出投影即可;
(2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系.计算可得DE=10(m).
解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°
∴△ABC∽△DEF.
∴,
∴
∴DE=10(m).
说明:画图时,不要求学生做文字说明,只要画出两条平行线AC和DF,再连接EF即可.
21.【分析】(1)以M、N为圆心,30为半径交于O点如图以线段MN、EF与、所围成的区域就是所作的A票区.2-1-c-n-j-y
(2)求座位就是求三角形EOF,MON和扇形FOM和EON的面积和.那么先求出扇形的半径即可.
解:(1)如图,以线段MN、EF与、所围成的区域就是所作的A票区.
(2)连接OM、ON、OE、OF,设MN的中垂线与MN、EF分别相交于点G和H.
由题意,得∠MON=90°.
∵OG⊥MN,OH⊥EF,
OG=OH=15,
∴∠EOF=∠MON=90°.
∴.
∴SA=(S扇形FOM+S扇形EON)+(S△OMN+S△EOF)=πr2+r2≈1125(米2).【版权所有:21教育】
∴1125÷0.8≈1406.
∴A票区约有1406个座位.
22.【分析】(1)由长方形中最长的线段为对角线,从而可根据已知运用勾股定理求得最长线段的长,又因为展开图形中有两个长方形,每个长方形有两条对角线,知这样的线段可画4条;21*cnjy*com
(2)要确定角的大小关系,一般把两个角分别放在两个三角形中,然后根据三角形的特点或者全等或者相似形来解.
解:(1)在平面展开图中可画出最长的线段长为,(1分)
如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,
∴.(3分)
答:这样的线段可画4条(另三条用虚线标出).(4分)
(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,∴∠BAC=45°.(5分)
在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'=,B'C'=.(7分)
又∵A′B′2+B′C′2=A′C′2,
由勾股定理的逆定理可得△A'B'C'为直角三角形.
又∵A′B′=B′C′,∴△A′B′C′为等腰直角三角形.(8分)
∴∠B′A′C′=45°.(9分)
∴∠BAC与∠B′A′C′相等.(10分)
23.【分析】考查立体图形的三视图,圆锥的表面积求法及公式的应用.
(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)圆锥的表面积等于扇形的表面积以及圆形的表面积之和;
(3)将圆锥的侧面展开,设顶点为B',连接BB',AC.线段AC与BB'的交点为D,线段BD是最短路程.
解:(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)表面积S=S扇形+S圆=+πr2
=πrR+πr2
=12π+4π
=16π(平方厘米),即该几何体全面积为16πcm2;
(3)如图将圆锥侧面展开,得到扇形ABB′,则线段BD为所求的最短路程.
设∠BAB′=n°.
∵=4π,
∴n=120即∠BAB′=120°.
∵C为弧BB′中点,
∴∠ADB=90°,∠BAD=60°,
∴BD=AB sin∠BAD=6×=cm,
∴路线的最短路程为3√3cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
投影与视图单元检测A卷
姓名:__________班级:__________学号:__________
一.选择题(共9小题)
1.正方形的正投影不可能是( )
A.线段 B.矩形 C.正方形 D.梯形
2.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
A.0.324πm2 B.0.288πm2 C.1.08πm2 D.0.72πm2
3.如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )21cnjy.com
A.E处 B.F处 C.G处 D.H处
4.下列图形中,可以是正方体表面展开图的是( )
A. B. C. D.
5.一个圆柱的侧面展开图是边长为a的正方形,则这个圆柱的体积为( )
A. B. C. D.
6.下列四个几何体中,主视图与左视图相同的几何体有( )
A.1个 B.2个 C.3个 D.4个
7.如图所示的几何体是由5个大小相同的小立方块搭成,它的俯视图是( )
A. B. C. D.
8.如图,是由若干个相同的小立方体搭成的几何体的俯视图和左视图.则小立方体的个数可能是( )
A.5或6 B.5或7 C.4或5或6 D.5或6或7
9.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是( )
A.(3)(1)(4)(2) B.(3)(2)(1)(4) C.(3)(4)(1)(2) D.(2)(4)(1)(3)
二.填空题(共7小题)
10.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为 m.2·1·c·n·j·y
11.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
12.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为 m.
13.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高 米.(结果保留根号)【来源:21·世纪·教育·网】
14.圆锥的主视图是边长为4cm的等边三角形,则该圆锥侧面展开图的面积是 cm2.
15.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .www-2-1-cnjy-com
16.如图,一个几何体的三视图分别是两个矩形、一个扇形,则这个几何体表面积的大小为 .
三.解答题(共7小题)
17.某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
18.5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是 (立方单位),表面积是 (平方单位)
(2)画出该几何体的主视图和左视图.
19.如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD.
(1)请你在图中画出路灯灯泡所在的位置(用点P表示);
(2)画出小华此时在路灯下的影子(用线段EF表示)
20.已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.21*cnjy*com
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
21.如图是某比赛场馆的平面图,根据距离比赛场地的远近和视角的不同,将观赛场地划分成A、B、C三个不同的票价区.其中与场地边缘MN的视角大于或等于45°,并且距场地边缘MN的距离不超过30m的区域划分为A票区,B票区如图所示,剩下的为C票区.(π取3)
(1)请你利用尺规作图,在观赛场地中,作出A票区所在的区域(只要作出图形,保留作图痕迹,不要求写作法);【来源:21cnj*y.co*m】
(2)如果每个座位所占的平均面积是0.8平方米,请估算A票区有多少个座位.
22.如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示.已知展开图中每个正方形的边长为1.21教育名师原创作品
(1)求在该展开图中可画出最长线段的长度这样的线段可画几条?
(2)试比较立体图中∠BAC与平面展开图中∠B′A′C′的大小关系?
23.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
答案与解析
一.选择题(共9小题)
1.【分析】根据平行投影的特点:在同一时刻,平行物体的投影仍旧平行,即可得出答案.
解:在同一时刻,平行物体的投影仍旧平行.得到的应是平行四边形或特殊的平行四边形或线段.
故正方形纸板ABCD的正投影不可能是梯形,
故选:D.
2.【分析】先根据AC⊥OB,BD⊥OB可得出△AOC∽△BOD,由相似三角形的对应边成比例可求出BD的长,进而得出BD′=0.3m,再由圆环的面积公式即可得出结论.
解:如图所示:∵AC⊥OB,BD⊥OB,
∴△AOC∽△BOD,
∴=,即=,
解得:BD=0.9m,
同理可得:AC′=0.2m,则BD′=0.3m,
∴S圆环形阴影=0.92 π﹣0.32π=0.72π(m2).
故选:D.
3.【分析】根据各选项安装位置判断能否覆盖所有空白部分即可.
解:如图,
A、若安装在E处,仍有区域:四边形MGNS和△PFI监控不到,此选项错误;
B、若安装在F处,仍有区域:△ERW监控不到,此选项错误;
C、若安装在G处,仍有区域:四边形QEWK监控不到,此选项错误;
D、若安装在H处,所有空白区域均能监控,此选项正确;
故选:D.
4.【分析】观察选项中的图形,确定出作为正方体表面展开图的即可.
解:下列图形中,可以是正方体表面展开图的是,
故选D
5.【分析】根据圆柱的侧面展开图确定出圆柱的底面半径与高,即可求出其体积.
解:根据题意得:()2π×a=,
故选A
6.【分析】主视图、左视图是分别从物体正面、左面看,所得到的图形.分别分析四种几何体的主视图与左视图,即可求解.21教育网
解:①正方体的主视图与左视图都是正方形;
②球的主视图与左视图都是圆;
③圆锥主视图与左视图都是三角形;
④圆柱的主视图和左视图都是长方形;
故选:D.
7.【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
解:从上面看易得横着的“”字,
故选C.
8.【分析】易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由左视图可得第二层最多和最少小立方体的个数,相加即可.www.21-cn-jy.com
解:由俯视图易得最底层有4个小立方体,由左视图易得第二层最多有3个小立方体和最少有1个小立方体,
那么小立方体的个数可能是5个或6个或7个.
故选D.
9.【分析】根据从早晨到傍晚物体影子的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.
解:西为(3),西北为(4),东北为(1),东为(2),
∴将它们按时间先后顺序排列为(3)(4)(1)(2).
故选:C.
二.填空题(共7小题)
10.【分析】根据题意,画出示意图,易得:Rt△EDC∽Rt△CDF,进而可得=;即DC2=ED FD,代入数据可得答案.
解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED FD,
代入数据可得DC2=16,
DC=4;
故答案为:4.
11.【分析】分两种情况:①底面周长为6高为16π;②底面周长为16π高为6;先根据底面周长得到底面半径,再根据圆柱的体积公式计算即可求解.
解:①底面周长为6高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
12.【分析】根据CD∥AB∥MN,得到△ABE∽△CDE,△ABF∽△MNF,根据相似三角形的性质可知,,即可得到结论.21·cn·jy·com
解:如图,∵CD∥AB∥MN,
∴△ABE∽△CDE,△ABF∽△MNF,
∴,,
即,,
解得:AB=3m.
答:路灯的高为3m.
13.【分析】设出树高,利用所给角的正切值分别表示出两次影子的长,然后作差建立方程即可.
解:如图,
在RtABC中,tan∠ACB=,
∴BC==,
同理:BD=,
∵两次测量的影长相差8米,
∴﹣=8,
∴x=4
故答案为4.
14.【分析】根据题意确定出圆锥的底面半径与母线,进而确定出侧面展开图面积即可.
解:根据题意得:圆锥的底面半径为2cm,母线长为4cm,
则该圆锥侧面展开图的面积是8πcm2.
故答案为:8π
15.【分析】根据从上边看得到的图形是俯视图,可得答案.
解:从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为:8.
16.【分析】由几何体的三视图得出该几何体的表面是由3个长方形与两个扇形围成,结合图中数据求出组合体的表面积即可.21世纪教育网版权所有
解:由几何体的三视图可得:
该几何体的表面是由3个长方形与两个扇形围成,
该几何体的表面积为:S=2×2×3+×2+×3=12+15π,
故答案为:12+15π.
三.解答题(共7小题)
17.【分析】考查立体图形的三视图,圆柱的全面积的求法及公式的应用.
解:(1)根据三视图的知识,主视图以及左视图都为矩形,俯视图是一个圆,故可判断出该几何体为圆柱.(2分)21·世纪*教育网
(2)根据圆柱的全面积公式可得,20π×40+2×π×102=1000π(6分).
18.【分析】(1)几何体的体积为5个正方体的体积和,表面积为20个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形(外面4个加里面2个),每个正方形的面积为1,【出处:21教育名师】
∴组合几何体的表面积为22.
故答案为:5,22;
(2)作图如下:
19.【分析】(1)根据小军和小丽的身高与影长即可得到光源所在;
(2)根据光源所在和小华的身高即可得到相应的影长.
解:如图所示:
(1)点P就是所求的点;
(2)EF就是小华此时在路灯下的影子.
20.【分析】(1)根据投影的定义,作出投影即可;
(2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系.计算可得DE=10(m).
解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°
∴△ABC∽△DEF.
∴,
∴
∴DE=10(m).
说明:画图时,不要求学生做文字说明,只要画出两条平行线AC和DF,再连接EF即可.
21.【分析】(1)以M、N为圆心,30为半径交于O点如图以线段MN、EF与、所围成的区域就是所作的A票区.2-1-c-n-j-y
(2)求座位就是求三角形EOF,MON和扇形FOM和EON的面积和.那么先求出扇形的半径即可.
解:(1)如图,以线段MN、EF与、所围成的区域就是所作的A票区.
(2)连接OM、ON、OE、OF,设MN的中垂线与MN、EF分别相交于点G和H.
由题意,得∠MON=90°.
∵OG⊥MN,OH⊥EF,
OG=OH=15,
∴∠EOF=∠MON=90°.
∴.
∴SA=(S扇形FOM+S扇形EON)+(S△OMN+S△EOF)=πr2+r2≈1125(米2).【版权所有:21教育】
∴1125÷0.8≈1406.
∴A票区约有1406个座位.
22.【分析】(1)由长方形中最长的线段为对角线,从而可根据已知运用勾股定理求得最长线段的长,又因为展开图形中有两个长方形,每个长方形有两条对角线,知这样的线段可画4条;21*cnjy*com
(2)要确定角的大小关系,一般把两个角分别放在两个三角形中,然后根据三角形的特点或者全等或者相似形来解.
解:(1)在平面展开图中可画出最长的线段长为,(1分)
如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,
∴.(3分)
答:这样的线段可画4条(另三条用虚线标出).(4分)
(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,∴∠BAC=45°.(5分)
在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'=,B'C'=.(7分)
又∵A′B′2+B′C′2=A′C′2,
由勾股定理的逆定理可得△A'B'C'为直角三角形.
又∵A′B′=B′C′,∴△A′B′C′为等腰直角三角形.(8分)
∴∠B′A′C′=45°.(9分)
∴∠BAC与∠B′A′C′相等.(10分)
23.【分析】考查立体图形的三视图,圆锥的表面积求法及公式的应用.
(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)圆锥的表面积等于扇形的表面积以及圆形的表面积之和;
(3)将圆锥的侧面展开,设顶点为B',连接BB',AC.线段AC与BB'的交点为D,线段BD是最短路程.
解:(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥;
(2)表面积S=S扇形+S圆=+πr2
=πrR+πr2
=12π+4π
=16π(平方厘米),即该几何体全面积为16πcm2;
(3)如图将圆锥侧面展开,得到扇形ABB′,则线段BD为所求的最短路程.
设∠BAB′=n°.
∵=4π,
∴n=120即∠BAB′=120°.
∵C为弧BB′中点,
∴∠ADB=90°,∠BAD=60°,
∴BD=AB sin∠BAD=6×=cm,
∴路线的最短路程为3√3cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
