第4章 概率单元检测A卷
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
概率单元检测A卷
姓名:__________班级:__________学号:__________
一.选择题(共10小题)
1.下列事件中,是必然事件的是( )
A.购买一张彩票,中奖 B.通常温度降到0℃以下,纯净的水结冰
C.明天一定是晴天 D.经过有交通信号灯的路口,遇到红灯
2.口袋中放有3只红球和11只黄球,这两种球除颜色外没有任何区别,随机从口袋中任取一只球,取得黄球的可能性的大小是( )
A. B. C. D.
3.对“某市明天下雨的概率是75%”这句话,理解正确的是( )
A.某市明天将有75%的时间下雨 B.某市明天将有75%的地区下雨
C.某市明天一定下雨 D.某市明天下雨的可能性较大
4.从,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )
A. B. C. D.
5.如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
A. B. C. D.
6.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )
A. B. C. D.
7.足球比赛前,裁判通常要掷一枚硬币来决定比赛双方的场地与首先发球者,其主要原因是( )
A.让比赛更富有情趣 B.让比赛更具有神秘色彩
C.体现比赛的公平性 D.让比赛更有挑战性
8.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( )
A.15个 B.20个 C.30个 D.35个
9.下列模拟掷硬币的实验不正确的是( )
A.用计算器随机地取数,取奇数相当于下面朝上,取偶数相当于硬币正面朝下
B.袋中装两个小球,分别标上1和2,随机地摸,摸出1表示硬币正面朝上
C.在没有大小王的扑克中随机地抽一张牌,抽到红色牌表示硬币正面朝上
D.将1、2、3、4、5分别写在5张纸上,并搓成团,每次随机地取一张,取到奇数号表示硬币正面朝上
10.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m﹣n|≤1,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
二.填空题(共8小题)
11.用长为4cm,5cm,6cm的三条线段围成三角形的事件,是 事件.
12.一只不透明的袋子中有1个白球、1个红球和2个黄球,这些球除颜色不同外其它都相同.搅均后从中任意摸出1个球,摸出白球可能性 摸出黄球可能性.(填“等于”或“小于”或“大于”).
13.某产品出现次品的概率为0.05,任意抽取这种产品600件,那么大约有 件是次品.
14.在一个不透明的布袋中装有4个白球和n个黄球,它们除颜色不同外,其余均相同,若从中随机摸出一个球,摸到黄球的概率是,则n= .
15.一只蚂蚁在如图所示的七巧板上任意爬行,已知它停在这副七巧板上的任何一点的可能性都相同,那么它停在1号板上的概率是 .
16.在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是 .
17.小华和小勇做抛掷2枚硬币游戏,抛1次.如果都“正面向上”,那么小华得1分;如果“一正一反”,那么小勇得1分;否则两人都得0分.谁先得到10分,谁就赢.对小华和小勇来讲,这个游戏规则公平吗?答: .
18.在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有 个.
三.解答题(共6小题)
19.中央电视台“幸运 52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不得奖,参与这个游戏的观众有三次翻牌机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是多少?
20.某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过摸球获得购物券.在一个不透明的盒子中放有20个除颜色外其余均相同的小球,其中有2个红球、3个绿球、5个黄球,其余是白球,规定顾客每购买100元的商品,就能获得一次摸球的机会,从盒子里摸出一个小球,如果摸到红球、绿球、黄球,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果摸到白球,那么就不能获得购物券.另一种方式是:不摸球,顾客每购买100元的商品,可直接获得25元购物券.
(1)顾客摸到白球的概率是多少?
(2)通过计算说明选择哪种方式更合算?
21.有一类随机事件概率的计算方法:设试验结果落在某个区域S中的每一点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事件A发生的概率P(A)=.有一块边长为30cm的正方形ABCD飞镖游戏板,假设飞镖投在游戏板上的每一点的机会均等.求下列事件发生的概率:
(1)在飞镖游戏板上画有半径为5cm的一个圆(如图1),求飞镖落在圆内的概率;
(2)飞镖在游戏板上的落点记为点O,求△OAB为钝角三角形的概率.
22.把一副扑克牌中的三张黑桃牌(它们的正面数字分别为3、4、5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字.当两张牌的牌面数字相同时,小王赢;当两张牌的牌面数字不同时,小李赢.现请你分析游戏规则对双方是否公平,并说明理由.
23.某射击运动员在相同条件下的射击160次,其成绩记录如下:
设计次数 20 40 60 80 100 120 140 160
射中九环以上的次数 15 33 63 79 97 111 130
射中九环以上的频率 0.75 0.83 0.80 0.79 0.79 0.79 0.81
(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),并简述理由.
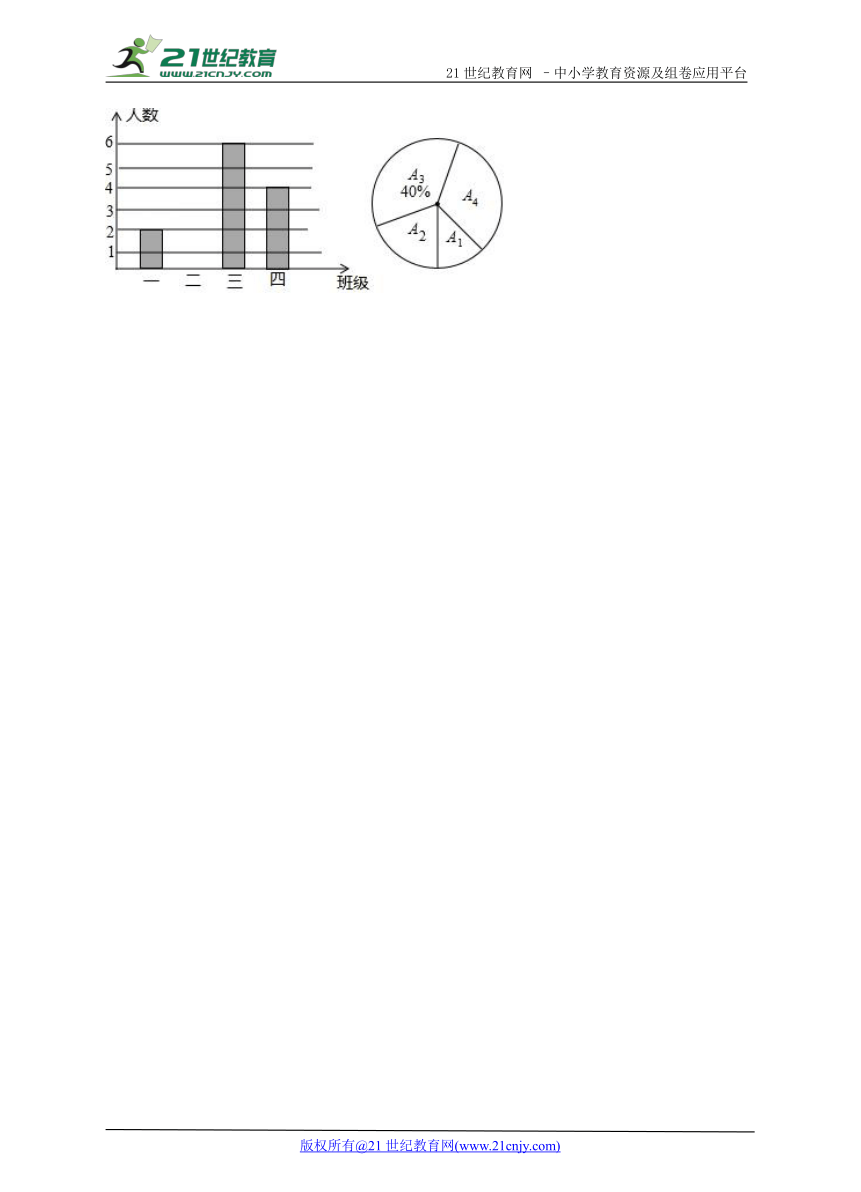
24.当前,“精准扶贫”工作已进入攻坚阶段,凡贫困家庭均要“建档立卡”.某初级中学七年级共有四个班,已“建档立卡”的贫困家庭的学生人数按一、二、三、四班分别记为A1,A2,A3,A4,现对A1,A2,A3,A4统计后,制成如图所示的统计图.
(1)求七年级已“建档立卡”的贫困家庭的学生总人数;
(2)将条形统计图补充完整,并求出A1所在扇形的圆心角的度数;
(3)现从A1,A2中各选出一人进行座谈,若A1中有一名女生,A2中有两名女生,请用树状图表示所有可能情况,并求出恰好选出一名男生和一名女生的概率.
答案解析
一.选择题
1.【分析】根据随机事件与必然事件的定义即可求出答案.
解:(A)购买一张彩票中奖是随机事件;
(B)根据物理学可知0℃以下,纯净的水结冰是必然事件;
(C)明天是晴天是随机事件;
(D)经过路口遇到红灯是随机事件;
故选(B)
2.【分析】计算出取得黄球的概率即可.
解:取得黄球的概率==,
所以随机从口袋中任取一只球,取得黄球的可能性的大小.
故选A.
3.【分析】根据概率的意义进行解答即可.
解:“某市明天下雨的概率是75%”说明某市明天下雨的可能性较大,
故选:D.
4.【分析】根据有理数的定义可找出在,0,π,3.14,6这5个数中只有0、3.14和6为有理数,再根据概率公式即可求出抽到有理数的概率.
解:∵在,0,π,3.14,6这5个数中只有0、3.14和6为有理数,
∴从,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是.
故选C.
5.【分析】根据正方形表面展开图的结构即可求出判断出构成这个正方体的表面展开图的概率.
解:设没有涂上阴影的分别为:A、B、C、D、E、F、G,如图所示,
从其余的小正方形中任取一个涂上阴影共有7种情况,
而能够构成正方体的表面展开图的有以下情况,D、E、F、G,
∴能构成这个正方体的表面展开图的概率是,
故选(A)
6.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球标号之和等于5的情况,再利用概率公式求解即可求得答案.
解:画树状图得:
∵共有12种等可能的结果,两次摸出的小球标号之和等于5的有4种情况,
∴两次摸出的小球标号之和等于5的概率是:=.
故选:C.
7.【分析】由正面朝上或朝下的概率均为,可得两个队选择场地与首先发球者的可能性相等,即体现比赛的公平性.
解:∵一枚硬币只有正反两面,
∴正面朝上或朝下的概率均为,
即两个队选择场地与首先发球者的可能性相等,
∴这种方法公平.
故选C.
8.【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设出未知数列出方程求解.
解:设袋中有黄球x个,由题意得=0.3,
解得x=15,则白球可能有50﹣15=35个.
故选D.
9.【分析】利用模拟实验只能用更简便方法完成,验证实验目的,但不能改变实验目的,进而分析得出即可.
解:A、用计算器随机地取数,取奇数相当于下面朝上,取偶数相当于硬币正面朝下,正确,不合题意;
B、袋中装两个小球,分别标上1和2,随机地摸,摸出1表示硬币正面朝上,正确,不合题意;
C、在没有大小王的扑克中随机地抽一张牌,抽到红色牌表示硬币正面朝上,正确,不合题意;
D、将1、2、3、4、5分别写在5张纸上,并搓成团,每次随机地取一张,取到奇数号表示硬币正面朝上,
由于奇数与偶数个数不相同,故不能模拟掷硬币的实验,故符合题意.
故选:D.
10.【分析】画出树状图列出所有等可能结果,由树状图确定出所有等可能结果数及两人“心领神会”的结果数,根据概率公式求解可得.
解:画树状图如下:
由树状图可知,共有16种等可能结果,其中满足|m﹣n|≤1的有10种结果,
∴两人“心领神会”的概率是=,
故选:B.
二.填空题
11.【分析】根据事件发生的可能性大小判断相应事件的类型即可.
解:根据三角形三边关系可知:4cm,5cm,6cm的三条线段一定能围成三角形,所以是必然事件.
12.【分析】先分别求出摸出各种颜色球的概率,再进行比较即可得出答案.
解:∵袋子中有1个白球、1个红球和2个黄球,共有4个球,
∴摸到白球的概率是,摸到红球的概率是,摸到黄球的概率是=,
∴摸出白球可能性<摸出黄球的可能性;
故答案为:小于.
13.【分析】利用总数×出现次品的概率=次品的数量,进而得出答案.
解:由题意可得:次品数量=600×0.05=30.
故答案为:30.
14.【分析】根据黄球的概率公式=列出方程求解即可.
解:不透明的布袋中的球除颜色不同外,其余均相同,共有n+4个球,其中黄球n个,
根据古典型概率公式知:P(黄球)==.
解得n=16.
故答案为:16.
15.【分析】首先确定在图中1号板的面积在整个面积中占的比例,根据这个比例即可求出蚂蚁停在1号板上的概率.
解:因为1号板的面积占了总面积的,故停在1号板上的概率=.
16.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所摸到1黑1白的情况,再利用概率公式即可求得答案.
解:依题意画树状图得:
∵共有6种等可能的结果,所摸到的球恰好为1黑1白的有4种情况,
∴所摸到的球恰好为1黑1白的概率是:=.
故答案为:.
17.【分析】游戏是否公平,只要计算出抛2次,如果2次“正面向上”和如果2次“反面向上”的概率是否相等,求出概率比较,即可得出结论.
解:如图所示:
,
根据概率的求法:任意抛掷一枚硬币两次,共4种情况;两次朝上的面都是正面只是其中的一种情况,
故P(小华赢)=,则P(小勇赢)=,比较得P(小华赢)=<P(小勇赢)=,故该游戏不公平.
故答案为:不公平.
18.【分析】由摸到红球的频率稳定在25%附近得出口袋中得到红色球的概率,进而求出白球个数即可.
解:设白球个数为:x个,
∵摸到红色球的频率稳定在25%左右,
∴口袋中得到红色球的概率为25%,
∴=,
解得:x=12,
故白球的个数为12个.
故答案为:12.
三.解答题
19.【分析】先求出20个商标中还剩的张数,再求出其中有奖的张数,最后根据概率公式进行计算即可.
解:∵20个商标中2个已翻出,还剩18张,18张中还有3张有奖的,
∴第三次翻牌获奖的概率是:.
20.【分析】(1)由在一个不透明的盒子里,装有20个大小形状完全相同的球,其中2个红球、3个绿球、5个黄球,其余是白球,直接利用概率公式求解即可求得答案;
(2)将摸球一次得到金额的平均数与直接获得购物券的金额数比较即可.
解:(1)∵在一个不透明的盒子里,装有20个大小形状完全相同的球,其中2个红球、3个绿球、5个黄球,其余是白球,
∴一次摸到白球的概率为:=;
(2)摸球对顾客更合算.
理由:∵一次摸到红球的概率为:;一次摸到绿球的概率为:;
一次摸到黄球的概率为:;一次摸到白球的概率为:,
又∵摸到红、黄、绿球的顾客就可以获得100元、50元、20元购物券,
∴摸球获得购物券钱数为:×100+×50+×20=22.5(元).
∵22.5<25,
∴直接获得25元购物券对顾客更合算.
21.【分析】(1)分别计算半径为5cm的圆的面积和边长为30cm的正方形ABCD的面积,然后计算即可求出飞镖落在圆内的概率;
(2)根据题意及结合图形可得:当点O落在以AB为直径的半圆内△OAB为钝角三角形,然后计算以AB为直径的半圆的面积,然后用半圆的面积除以正方形的面积即可求△OAB为钝角三角形的概率.
解:(1)∵半径为5cm的圆的面积=π 52=25πcm2,
边长为30cm的正方形ABCD的面积=302=900cm2,
∴P(飞镖落在圆内)===;
(2)如图可得:当点O落在以AB为直径的半圆内△OAB为钝角三角形.
∵S半圆= π 152=,
∴P(△OAB为钝角三角形)==.
22.【分析】该游戏不公平,理由为:列表得出所有等可能的情况数,找出数字相同的情况数,分别求出两人获胜的概率,比较即可.
解:该游戏不公平,理由为:
列表如下:
3 4 5
3 (3,3) (4,3) (5,3)
4 (3,4) (4,4) (5,4)
5 (3,5) (4,5) (5,5)
两人各抽取一张牌,总共有9种情况,分别为:(3,3);(3,4);(3,5);(4,3);(4,4);(4,5);(5,3),(5,4),(5,5),
其中数字相同的有3种情况,分别为(3,3);(4,4);(5,5),
∴P(小王赢)==,P(小李赢)==,
∵P(小王赢)<P(小李赢),
∴游戏规则不公平.
23.【分析】根据频数的计算方法计算即可.
解:(1)48,0.81;
(2)P(射中9环以上)=0.8
从频率的波动情况可以发现频率稳定在0.8附近,所以这名运动员射击一次时“射中9环以上”的概率是0.8.
24.【分析】(1)根据A3的人数除以A3所占的百分比即可求出总人数.
(2)根据A1的人数的所占的百分比即可取出圆心角的度数.
(3)列出树状图即可求出答案.
解:(1)总数人数为:6÷40%=15人
(2)A2的人数为15﹣2﹣6﹣4=3(人)
补全图形,如图所示
A1所在圆心角度数为:×360°=48°
(3)画出树状图如下:
故所求概率为:P==
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
概率单元检测A卷
姓名:__________班级:__________学号:__________
一.选择题(共10小题)
1.下列事件中,是必然事件的是( )
A.购买一张彩票,中奖 B.通常温度降到0℃以下,纯净的水结冰
C.明天一定是晴天 D.经过有交通信号灯的路口,遇到红灯
2.口袋中放有3只红球和11只黄球,这两种球除颜色外没有任何区别,随机从口袋中任取一只球,取得黄球的可能性的大小是( )
A. B. C. D.
3.对“某市明天下雨的概率是75%”这句话,理解正确的是( )
A.某市明天将有75%的时间下雨 B.某市明天将有75%的地区下雨
C.某市明天一定下雨 D.某市明天下雨的可能性较大
4.从,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )
A. B. C. D.
5.如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
A. B. C. D.
6.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )
A. B. C. D.
7.足球比赛前,裁判通常要掷一枚硬币来决定比赛双方的场地与首先发球者,其主要原因是( )
A.让比赛更富有情趣 B.让比赛更具有神秘色彩
C.体现比赛的公平性 D.让比赛更有挑战性
8.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( )
A.15个 B.20个 C.30个 D.35个
9.下列模拟掷硬币的实验不正确的是( )
A.用计算器随机地取数,取奇数相当于下面朝上,取偶数相当于硬币正面朝下
B.袋中装两个小球,分别标上1和2,随机地摸,摸出1表示硬币正面朝上
C.在没有大小王的扑克中随机地抽一张牌,抽到红色牌表示硬币正面朝上
D.将1、2、3、4、5分别写在5张纸上,并搓成团,每次随机地取一张,取到奇数号表示硬币正面朝上
10.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m﹣n|≤1,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
二.填空题(共8小题)
11.用长为4cm,5cm,6cm的三条线段围成三角形的事件,是 事件.
12.一只不透明的袋子中有1个白球、1个红球和2个黄球,这些球除颜色不同外其它都相同.搅均后从中任意摸出1个球,摸出白球可能性 摸出黄球可能性.(填“等于”或“小于”或“大于”).
13.某产品出现次品的概率为0.05,任意抽取这种产品600件,那么大约有 件是次品.
14.在一个不透明的布袋中装有4个白球和n个黄球,它们除颜色不同外,其余均相同,若从中随机摸出一个球,摸到黄球的概率是,则n= .
15.一只蚂蚁在如图所示的七巧板上任意爬行,已知它停在这副七巧板上的任何一点的可能性都相同,那么它停在1号板上的概率是 .
16.在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是 .
17.小华和小勇做抛掷2枚硬币游戏,抛1次.如果都“正面向上”,那么小华得1分;如果“一正一反”,那么小勇得1分;否则两人都得0分.谁先得到10分,谁就赢.对小华和小勇来讲,这个游戏规则公平吗?答: .
18.在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有 个.
三.解答题(共6小题)
19.中央电视台“幸运 52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不得奖,参与这个游戏的观众有三次翻牌机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是多少?
20.某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过摸球获得购物券.在一个不透明的盒子中放有20个除颜色外其余均相同的小球,其中有2个红球、3个绿球、5个黄球,其余是白球,规定顾客每购买100元的商品,就能获得一次摸球的机会,从盒子里摸出一个小球,如果摸到红球、绿球、黄球,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果摸到白球,那么就不能获得购物券.另一种方式是:不摸球,顾客每购买100元的商品,可直接获得25元购物券.
(1)顾客摸到白球的概率是多少?
(2)通过计算说明选择哪种方式更合算?
21.有一类随机事件概率的计算方法:设试验结果落在某个区域S中的每一点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事件A发生的概率P(A)=.有一块边长为30cm的正方形ABCD飞镖游戏板,假设飞镖投在游戏板上的每一点的机会均等.求下列事件发生的概率:
(1)在飞镖游戏板上画有半径为5cm的一个圆(如图1),求飞镖落在圆内的概率;
(2)飞镖在游戏板上的落点记为点O,求△OAB为钝角三角形的概率.
22.把一副扑克牌中的三张黑桃牌(它们的正面数字分别为3、4、5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字.当两张牌的牌面数字相同时,小王赢;当两张牌的牌面数字不同时,小李赢.现请你分析游戏规则对双方是否公平,并说明理由.
23.某射击运动员在相同条件下的射击160次,其成绩记录如下:
设计次数 20 40 60 80 100 120 140 160
射中九环以上的次数 15 33 63 79 97 111 130
射中九环以上的频率 0.75 0.83 0.80 0.79 0.79 0.79 0.81
(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),并简述理由.
24.当前,“精准扶贫”工作已进入攻坚阶段,凡贫困家庭均要“建档立卡”.某初级中学七年级共有四个班,已“建档立卡”的贫困家庭的学生人数按一、二、三、四班分别记为A1,A2,A3,A4,现对A1,A2,A3,A4统计后,制成如图所示的统计图.
(1)求七年级已“建档立卡”的贫困家庭的学生总人数;
(2)将条形统计图补充完整,并求出A1所在扇形的圆心角的度数;
(3)现从A1,A2中各选出一人进行座谈,若A1中有一名女生,A2中有两名女生,请用树状图表示所有可能情况,并求出恰好选出一名男生和一名女生的概率.
答案解析
一.选择题
1.【分析】根据随机事件与必然事件的定义即可求出答案.
解:(A)购买一张彩票中奖是随机事件;
(B)根据物理学可知0℃以下,纯净的水结冰是必然事件;
(C)明天是晴天是随机事件;
(D)经过路口遇到红灯是随机事件;
故选(B)
2.【分析】计算出取得黄球的概率即可.
解:取得黄球的概率==,
所以随机从口袋中任取一只球,取得黄球的可能性的大小.
故选A.
3.【分析】根据概率的意义进行解答即可.
解:“某市明天下雨的概率是75%”说明某市明天下雨的可能性较大,
故选:D.
4.【分析】根据有理数的定义可找出在,0,π,3.14,6这5个数中只有0、3.14和6为有理数,再根据概率公式即可求出抽到有理数的概率.
解:∵在,0,π,3.14,6这5个数中只有0、3.14和6为有理数,
∴从,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是.
故选C.
5.【分析】根据正方形表面展开图的结构即可求出判断出构成这个正方体的表面展开图的概率.
解:设没有涂上阴影的分别为:A、B、C、D、E、F、G,如图所示,
从其余的小正方形中任取一个涂上阴影共有7种情况,
而能够构成正方体的表面展开图的有以下情况,D、E、F、G,
∴能构成这个正方体的表面展开图的概率是,
故选(A)
6.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球标号之和等于5的情况,再利用概率公式求解即可求得答案.
解:画树状图得:
∵共有12种等可能的结果,两次摸出的小球标号之和等于5的有4种情况,
∴两次摸出的小球标号之和等于5的概率是:=.
故选:C.
7.【分析】由正面朝上或朝下的概率均为,可得两个队选择场地与首先发球者的可能性相等,即体现比赛的公平性.
解:∵一枚硬币只有正反两面,
∴正面朝上或朝下的概率均为,
即两个队选择场地与首先发球者的可能性相等,
∴这种方法公平.
故选C.
8.【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设出未知数列出方程求解.
解:设袋中有黄球x个,由题意得=0.3,
解得x=15,则白球可能有50﹣15=35个.
故选D.
9.【分析】利用模拟实验只能用更简便方法完成,验证实验目的,但不能改变实验目的,进而分析得出即可.
解:A、用计算器随机地取数,取奇数相当于下面朝上,取偶数相当于硬币正面朝下,正确,不合题意;
B、袋中装两个小球,分别标上1和2,随机地摸,摸出1表示硬币正面朝上,正确,不合题意;
C、在没有大小王的扑克中随机地抽一张牌,抽到红色牌表示硬币正面朝上,正确,不合题意;
D、将1、2、3、4、5分别写在5张纸上,并搓成团,每次随机地取一张,取到奇数号表示硬币正面朝上,
由于奇数与偶数个数不相同,故不能模拟掷硬币的实验,故符合题意.
故选:D.
10.【分析】画出树状图列出所有等可能结果,由树状图确定出所有等可能结果数及两人“心领神会”的结果数,根据概率公式求解可得.
解:画树状图如下:
由树状图可知,共有16种等可能结果,其中满足|m﹣n|≤1的有10种结果,
∴两人“心领神会”的概率是=,
故选:B.
二.填空题
11.【分析】根据事件发生的可能性大小判断相应事件的类型即可.
解:根据三角形三边关系可知:4cm,5cm,6cm的三条线段一定能围成三角形,所以是必然事件.
12.【分析】先分别求出摸出各种颜色球的概率,再进行比较即可得出答案.
解:∵袋子中有1个白球、1个红球和2个黄球,共有4个球,
∴摸到白球的概率是,摸到红球的概率是,摸到黄球的概率是=,
∴摸出白球可能性<摸出黄球的可能性;
故答案为:小于.
13.【分析】利用总数×出现次品的概率=次品的数量,进而得出答案.
解:由题意可得:次品数量=600×0.05=30.
故答案为:30.
14.【分析】根据黄球的概率公式=列出方程求解即可.
解:不透明的布袋中的球除颜色不同外,其余均相同,共有n+4个球,其中黄球n个,
根据古典型概率公式知:P(黄球)==.
解得n=16.
故答案为:16.
15.【分析】首先确定在图中1号板的面积在整个面积中占的比例,根据这个比例即可求出蚂蚁停在1号板上的概率.
解:因为1号板的面积占了总面积的,故停在1号板上的概率=.
16.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所摸到1黑1白的情况,再利用概率公式即可求得答案.
解:依题意画树状图得:
∵共有6种等可能的结果,所摸到的球恰好为1黑1白的有4种情况,
∴所摸到的球恰好为1黑1白的概率是:=.
故答案为:.
17.【分析】游戏是否公平,只要计算出抛2次,如果2次“正面向上”和如果2次“反面向上”的概率是否相等,求出概率比较,即可得出结论.
解:如图所示:
,
根据概率的求法:任意抛掷一枚硬币两次,共4种情况;两次朝上的面都是正面只是其中的一种情况,
故P(小华赢)=,则P(小勇赢)=,比较得P(小华赢)=<P(小勇赢)=,故该游戏不公平.
故答案为:不公平.
18.【分析】由摸到红球的频率稳定在25%附近得出口袋中得到红色球的概率,进而求出白球个数即可.
解:设白球个数为:x个,
∵摸到红色球的频率稳定在25%左右,
∴口袋中得到红色球的概率为25%,
∴=,
解得:x=12,
故白球的个数为12个.
故答案为:12.
三.解答题
19.【分析】先求出20个商标中还剩的张数,再求出其中有奖的张数,最后根据概率公式进行计算即可.
解:∵20个商标中2个已翻出,还剩18张,18张中还有3张有奖的,
∴第三次翻牌获奖的概率是:.
20.【分析】(1)由在一个不透明的盒子里,装有20个大小形状完全相同的球,其中2个红球、3个绿球、5个黄球,其余是白球,直接利用概率公式求解即可求得答案;
(2)将摸球一次得到金额的平均数与直接获得购物券的金额数比较即可.
解:(1)∵在一个不透明的盒子里,装有20个大小形状完全相同的球,其中2个红球、3个绿球、5个黄球,其余是白球,
∴一次摸到白球的概率为:=;
(2)摸球对顾客更合算.
理由:∵一次摸到红球的概率为:;一次摸到绿球的概率为:;
一次摸到黄球的概率为:;一次摸到白球的概率为:,
又∵摸到红、黄、绿球的顾客就可以获得100元、50元、20元购物券,
∴摸球获得购物券钱数为:×100+×50+×20=22.5(元).
∵22.5<25,
∴直接获得25元购物券对顾客更合算.
21.【分析】(1)分别计算半径为5cm的圆的面积和边长为30cm的正方形ABCD的面积,然后计算即可求出飞镖落在圆内的概率;
(2)根据题意及结合图形可得:当点O落在以AB为直径的半圆内△OAB为钝角三角形,然后计算以AB为直径的半圆的面积,然后用半圆的面积除以正方形的面积即可求△OAB为钝角三角形的概率.
解:(1)∵半径为5cm的圆的面积=π 52=25πcm2,
边长为30cm的正方形ABCD的面积=302=900cm2,
∴P(飞镖落在圆内)===;
(2)如图可得:当点O落在以AB为直径的半圆内△OAB为钝角三角形.
∵S半圆= π 152=,
∴P(△OAB为钝角三角形)==.
22.【分析】该游戏不公平,理由为:列表得出所有等可能的情况数,找出数字相同的情况数,分别求出两人获胜的概率,比较即可.
解:该游戏不公平,理由为:
列表如下:
3 4 5
3 (3,3) (4,3) (5,3)
4 (3,4) (4,4) (5,4)
5 (3,5) (4,5) (5,5)
两人各抽取一张牌,总共有9种情况,分别为:(3,3);(3,4);(3,5);(4,3);(4,4);(4,5);(5,3),(5,4),(5,5),
其中数字相同的有3种情况,分别为(3,3);(4,4);(5,5),
∴P(小王赢)==,P(小李赢)==,
∵P(小王赢)<P(小李赢),
∴游戏规则不公平.
23.【分析】根据频数的计算方法计算即可.
解:(1)48,0.81;
(2)P(射中9环以上)=0.8
从频率的波动情况可以发现频率稳定在0.8附近,所以这名运动员射击一次时“射中9环以上”的概率是0.8.
24.【分析】(1)根据A3的人数除以A3所占的百分比即可求出总人数.
(2)根据A1的人数的所占的百分比即可取出圆心角的度数.
(3)列出树状图即可求出答案.
解:(1)总数人数为:6÷40%=15人
(2)A2的人数为15﹣2﹣6﹣4=3(人)
补全图形,如图所示
A1所在圆心角度数为:×360°=48°
(3)画出树状图如下:
故所求概率为:P==
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
