2017-2018学年高中数学人教B版必修4课时作业:第一章基本初等函Ⅱ学业水平达标检测+Word版含答案
文档属性
| 名称 | 2017-2018学年高中数学人教B版必修4课时作业:第一章基本初等函Ⅱ学业水平达标检测+Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-30 00:00:00 | ||
图片预览




文档简介
第一章 基本初等函(Ⅱ)
学业水平达标检测
时间:120分钟 满分:150分
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设α为第二象限角,且有=-cos,则为( )
A.第一象限角 B.第二象限角
C.第三象限角
D.第四象限角
解析:∵α是第二象限角,∴+2kπ<α<π+2kπ,k∈Z,∴+kπ<<+kπ,k∈Z,∴的终边在第一象限或第三象限.又∵=-cos,∴cos≤0,∴是第三象限角.
答案:C
2.下列函数中,最小正周期为的是( )
A.y=sin
B.y=tan
C.y=cos
D.y=tan
解析:A选项的最小正周期是π,B选项的最小正周期是,C选项的最小正周期是π,D选项的最小正周期是.
答案:B
3.将函数y=sin4x的图象向左平移个单位长度,得到y=sin(4x+φ)的图象,则φ等于( )
A.-
B.-
C.
D.
解析:将函数y=sin4x的图象向左平移个单位长度,得到函数y=sin=sin的图象,∴φ=.
答案:C
4.设M和m分别表示函数y=cosx-1的最大值和最小值,则M+m等于( )
A.
B.-
C.-
D.-2
解析:依题意,M=-1=-,m=--1=-,∴M+m=-2.
答案:D
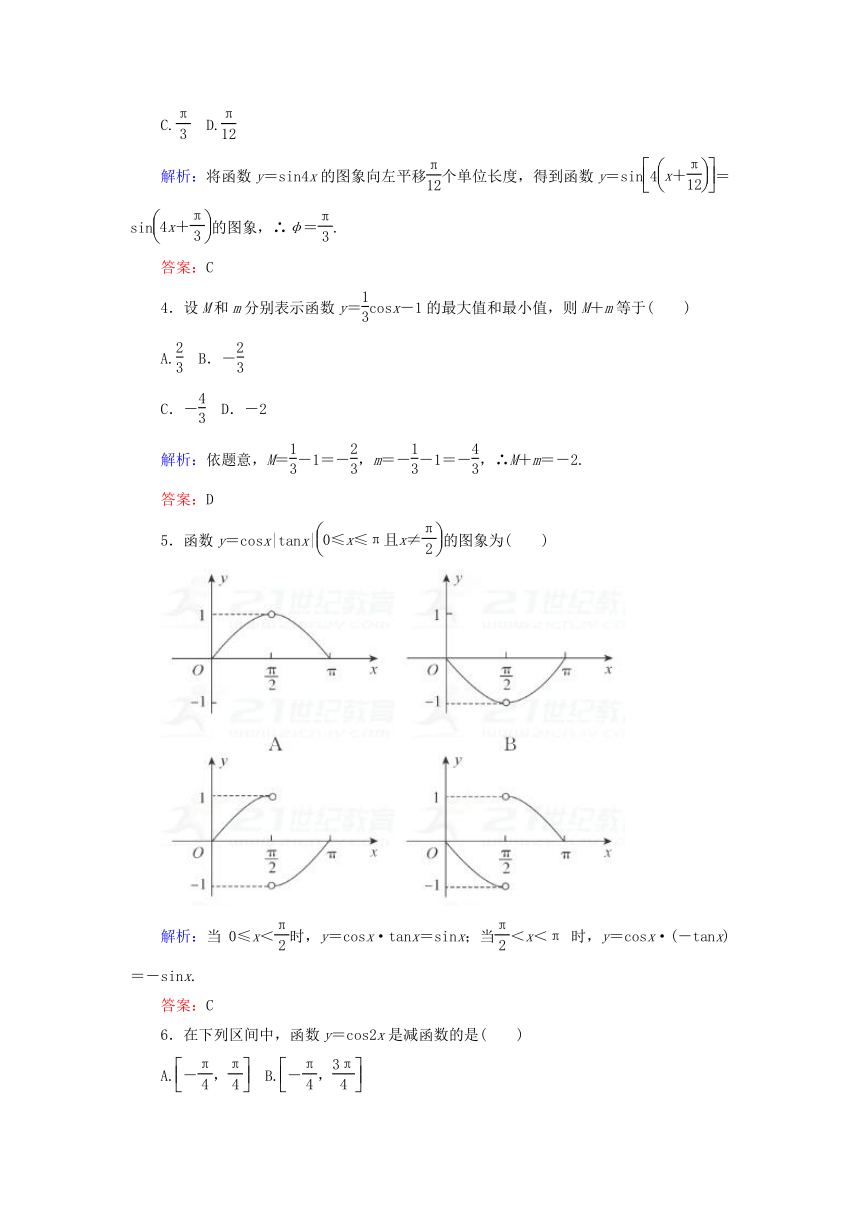
5.函数y=cosx|tanx|的图象为( )
解析:当0≤x<时,y=cosx·tanx=sinx;当<x<π时,y=cosx·(-tanx)=-sinx.
答案:C
6.在下列区间中,函数y=cos2x是减函数的是( )
A.
B.
C.
D.
解析:令0≤2x≤π,解得0≤x≤.
答案:C
7.在下面给出的四个函数中,既是区间上的增函数,又是以π为周期的偶函数的是( )
A.y=cos2x
B.y=sin2x
C.y=|cosx|
D.y=|sinx|
解析:∵函数在上是增函数,∴选D.
答案:D
8.已知θ是第三象限角,且sin4θ+cos4θ=,则sinθ·cosθ=( )
A.
B.-
C.
D.-
解析:sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θ·cos2θ=1-2sin2θcos2θ=,∴sin2θcos2θ=.
∵θ是第三象限角,∴sinθcosθ>0,∴sinθcosθ=.
答案:A
9.函数f(x)=sin的图象的一条对称轴是( )
A.x=
B.x=
C.x=-
D.x=-
解析:根据正弦曲线的特征求解.
∵正弦函数图象的对称轴过图象的最高点或最低点,
故令x-=kπ+,k∈Z,∴x=kπ+,k∈Z.
取k=-1,则x=-.
答案:C
10.y=2sin的单调递增区间为( )
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
解析:∵y=2sin=-2sin.
∴令+2kπ≤2x-≤+2kπ,k∈Z,
解得+kπ≤x≤+kπ,k∈Z.
答案:B
11.若sinx=,x∈,则角x为( )
A.arcsin
B.π-arcsin
C.+arcsin
D.-arcsin
解析:∵x∈,∴π-x∈.
又∵sinx=,∴sin(π-x)=sinx=.
∴π-x=arcsin,∴x=π-arcsin.
答案:B
12.为了得到y=sin2x的图象,只需将y=sin的图象( )
A.向右平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向左平移个单位长度
解析:y=sin=sin2,
sin2=sin2x,只需向右平移个单位长度即可得到y=sin2x的图象,注意将系数提出并注意平移的方向.
答案:B
二、填空题:本大题共4小题,每小题5分,共20分.
13.函数y=+的定义域为__________.
解析:由题意,得
∴用数轴表示,如图.
∴0<x<或π≤x≤4.
答案:∪[π,4]
14.把函数y=cos的图象向左平移m(m>0)个单位长度,所得图象关于y轴对称,则m的最小值是__________.
解析:将函数y=cos的图象向左平移m个单位长度,得到函数y=cos的图象,
因为y=cos的图象关于y轴对称,
所以m+=kπ,k∈Z.∴m=kπ-,k∈Z.
又m>0,∴m的最小值为.
答案:
15.如图是函数y=Asin(ωx+φ)(A,ω>0,0<φ<π)的图象的一段,它的解析式为__________.
解析:由图象知A=,T=2=π,∴ω==2,由五点作图知-×2+φ=,∴φ=,∴y=sin.
答案:y=sin
16.关于函数f(x)=4sin(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是的整数倍;
②函数y=f(x)的表达式可以改写为f(x)=4cos(x∈R);
③其图象可由y=4sin2x的图象向左平移个单位长度得到;
④函数y=f(x)的图象关于点对称;
⑤在x∈上为增函数.
其中,正确命题的序号是__________.
解析:满足f(x1)=f(x2)=0的x1与x2间相差为半个周期的整数倍,故①正确;f(x)=4sin=4cos=4cos=4cos,故②正确;将y=4sin2x的图象向左平移个单位长度,得到函数y=4sin,故③错误;∵f=4sin0=0,故④正确;当x∈时,2x+∈,故⑤错误.
答案:①②④
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.已知tan(π+α)=3,求:
(1);
(2)sin2α+2sinαcosα.
解析:tan(π+α)=tanα=3.
(1)原式====7.
(2)原式====.
18.当x∈时,求函数y=3-sinx-2cos2x的最值.
解析:由题意知y=3-sinx-2+2sin2x=2sin2x-sinx+1=
22+.
∵≤x≤,∴-≤sinx≤1,即sinx=时,ymin=;
sinx=-或sinx=1时,ymax=2.
19.用“五点法”在图中作出函数y=sin的图象.
(1)求函数的最小正周期;
(2)求函数的最大值、最小值及相应x的值;
(3)函数y=sin的图象可由函数y=sinx的图象怎样变换得到?
解析:列表:
x
-
π
π
2x+
0
π
π
2π
y
0
1
0
-1
0
图象如图.
(1)T==π.
(2)当2x+=2kπ+,即x=kπ+,k∈Z时,ymax=1;
当2x+=2kπ-,
即x=kπ-π,k∈Z时,ymin=-1.
(3)(方法一)y=sinxy=siny=sin.
(方法二)y=sinxy=sin2xy=sin=sin.
20.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内,当x=时,y有最大值为2,当x=时,y有最小值为-2.
(1)求函数f(x)的表达式;
(2)若g(x)=f(-x),求g(x)的单调减区间.
解析:(1)∵当x=时,y有最大值2,当x=时,y有最小值-2,
∴=-=,
∴T=π,ω===2,A=2.
将代入f(x)=2sin(2x+φ)解得φ=,
∴函数f(x)=2sin.
(2)g(x)=2sin=-2sin,
由-+2kπ≤2x-≤+2kπ,k∈Z得
-+kπ≤x≤+kπ,k∈Z,
∴g(x)的单调减区间为(k∈Z).
21.已知cos=cos,sin=-sin,且0<α<π,0<β<π,求α,β的值.
解析:由题意,得
①2+②2,得sin2α+3cos2α=2.
又sin2α+cos2α=1,∴sin2α=,即sinα=±.
又∵0<α<π,∴sinα=,即α=或π.
当α=时,cosβ=·,即cosβ=,即β=;
当α=π时,cosβ=×,
即cosβ=-,即β=π.∴或
22.f(x)=2sin(ω>0).
(1)若f(x+θ)是周期为2π的偶函数,求ω及θ的值;
(2)若f(x)在上单调递增,求ω的最大值.
解析:(1)f(x+θ)=2sin
=2sin,
∵T=2π,∴=2π,即ω=.
又f(x+θ)为偶函数,
∴3ωθ+=kπ+(k∈Z),即θ=kπ+(k∈Z).
(2)令2kπ-≤3ωx+≤2kπ+,则
≤x≤,k∈Z.
故单调递增区间为.
∵f(x)在上单调递增,
∴ (k∈Z).
即解得
∴k=0时,ωmax=.
学业水平达标检测
时间:120分钟 满分:150分
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设α为第二象限角,且有=-cos,则为( )
A.第一象限角 B.第二象限角
C.第三象限角
D.第四象限角
解析:∵α是第二象限角,∴+2kπ<α<π+2kπ,k∈Z,∴+kπ<<+kπ,k∈Z,∴的终边在第一象限或第三象限.又∵=-cos,∴cos≤0,∴是第三象限角.
答案:C
2.下列函数中,最小正周期为的是( )
A.y=sin
B.y=tan
C.y=cos
D.y=tan
解析:A选项的最小正周期是π,B选项的最小正周期是,C选项的最小正周期是π,D选项的最小正周期是.
答案:B
3.将函数y=sin4x的图象向左平移个单位长度,得到y=sin(4x+φ)的图象,则φ等于( )
A.-
B.-
C.
D.
解析:将函数y=sin4x的图象向左平移个单位长度,得到函数y=sin=sin的图象,∴φ=.
答案:C
4.设M和m分别表示函数y=cosx-1的最大值和最小值,则M+m等于( )
A.
B.-
C.-
D.-2
解析:依题意,M=-1=-,m=--1=-,∴M+m=-2.
答案:D
5.函数y=cosx|tanx|的图象为( )
解析:当0≤x<时,y=cosx·tanx=sinx;当<x<π时,y=cosx·(-tanx)=-sinx.
答案:C
6.在下列区间中,函数y=cos2x是减函数的是( )
A.
B.
C.
D.
解析:令0≤2x≤π,解得0≤x≤.
答案:C
7.在下面给出的四个函数中,既是区间上的增函数,又是以π为周期的偶函数的是( )
A.y=cos2x
B.y=sin2x
C.y=|cosx|
D.y=|sinx|
解析:∵函数在上是增函数,∴选D.
答案:D
8.已知θ是第三象限角,且sin4θ+cos4θ=,则sinθ·cosθ=( )
A.
B.-
C.
D.-
解析:sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θ·cos2θ=1-2sin2θcos2θ=,∴sin2θcos2θ=.
∵θ是第三象限角,∴sinθcosθ>0,∴sinθcosθ=.
答案:A
9.函数f(x)=sin的图象的一条对称轴是( )
A.x=
B.x=
C.x=-
D.x=-
解析:根据正弦曲线的特征求解.
∵正弦函数图象的对称轴过图象的最高点或最低点,
故令x-=kπ+,k∈Z,∴x=kπ+,k∈Z.
取k=-1,则x=-.
答案:C
10.y=2sin的单调递增区间为( )
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
解析:∵y=2sin=-2sin.
∴令+2kπ≤2x-≤+2kπ,k∈Z,
解得+kπ≤x≤+kπ,k∈Z.
答案:B
11.若sinx=,x∈,则角x为( )
A.arcsin
B.π-arcsin
C.+arcsin
D.-arcsin
解析:∵x∈,∴π-x∈.
又∵sinx=,∴sin(π-x)=sinx=.
∴π-x=arcsin,∴x=π-arcsin.
答案:B
12.为了得到y=sin2x的图象,只需将y=sin的图象( )
A.向右平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向左平移个单位长度
解析:y=sin=sin2,
sin2=sin2x,只需向右平移个单位长度即可得到y=sin2x的图象,注意将系数提出并注意平移的方向.
答案:B
二、填空题:本大题共4小题,每小题5分,共20分.
13.函数y=+的定义域为__________.
解析:由题意,得
∴用数轴表示,如图.
∴0<x<或π≤x≤4.
答案:∪[π,4]
14.把函数y=cos的图象向左平移m(m>0)个单位长度,所得图象关于y轴对称,则m的最小值是__________.
解析:将函数y=cos的图象向左平移m个单位长度,得到函数y=cos的图象,
因为y=cos的图象关于y轴对称,
所以m+=kπ,k∈Z.∴m=kπ-,k∈Z.
又m>0,∴m的最小值为.
答案:
15.如图是函数y=Asin(ωx+φ)(A,ω>0,0<φ<π)的图象的一段,它的解析式为__________.
解析:由图象知A=,T=2=π,∴ω==2,由五点作图知-×2+φ=,∴φ=,∴y=sin.
答案:y=sin
16.关于函数f(x)=4sin(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是的整数倍;
②函数y=f(x)的表达式可以改写为f(x)=4cos(x∈R);
③其图象可由y=4sin2x的图象向左平移个单位长度得到;
④函数y=f(x)的图象关于点对称;
⑤在x∈上为增函数.
其中,正确命题的序号是__________.
解析:满足f(x1)=f(x2)=0的x1与x2间相差为半个周期的整数倍,故①正确;f(x)=4sin=4cos=4cos=4cos,故②正确;将y=4sin2x的图象向左平移个单位长度,得到函数y=4sin,故③错误;∵f=4sin0=0,故④正确;当x∈时,2x+∈,故⑤错误.
答案:①②④
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.已知tan(π+α)=3,求:
(1);
(2)sin2α+2sinαcosα.
解析:tan(π+α)=tanα=3.
(1)原式====7.
(2)原式====.
18.当x∈时,求函数y=3-sinx-2cos2x的最值.
解析:由题意知y=3-sinx-2+2sin2x=2sin2x-sinx+1=
22+.
∵≤x≤,∴-≤sinx≤1,即sinx=时,ymin=;
sinx=-或sinx=1时,ymax=2.
19.用“五点法”在图中作出函数y=sin的图象.
(1)求函数的最小正周期;
(2)求函数的最大值、最小值及相应x的值;
(3)函数y=sin的图象可由函数y=sinx的图象怎样变换得到?
解析:列表:
x
-
π
π
2x+
0
π
π
2π
y
0
1
0
-1
0
图象如图.
(1)T==π.
(2)当2x+=2kπ+,即x=kπ+,k∈Z时,ymax=1;
当2x+=2kπ-,
即x=kπ-π,k∈Z时,ymin=-1.
(3)(方法一)y=sinxy=siny=sin.
(方法二)y=sinxy=sin2xy=sin=sin.
20.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内,当x=时,y有最大值为2,当x=时,y有最小值为-2.
(1)求函数f(x)的表达式;
(2)若g(x)=f(-x),求g(x)的单调减区间.
解析:(1)∵当x=时,y有最大值2,当x=时,y有最小值-2,
∴=-=,
∴T=π,ω===2,A=2.
将代入f(x)=2sin(2x+φ)解得φ=,
∴函数f(x)=2sin.
(2)g(x)=2sin=-2sin,
由-+2kπ≤2x-≤+2kπ,k∈Z得
-+kπ≤x≤+kπ,k∈Z,
∴g(x)的单调减区间为(k∈Z).
21.已知cos=cos,sin=-sin,且0<α<π,0<β<π,求α,β的值.
解析:由题意,得
①2+②2,得sin2α+3cos2α=2.
又sin2α+cos2α=1,∴sin2α=,即sinα=±.
又∵0<α<π,∴sinα=,即α=或π.
当α=时,cosβ=·,即cosβ=,即β=;
当α=π时,cosβ=×,
即cosβ=-,即β=π.∴或
22.f(x)=2sin(ω>0).
(1)若f(x+θ)是周期为2π的偶函数,求ω及θ的值;
(2)若f(x)在上单调递增,求ω的最大值.
解析:(1)f(x+θ)=2sin
=2sin,
∵T=2π,∴=2π,即ω=.
又f(x+θ)为偶函数,
∴3ωθ+=kπ+(k∈Z),即θ=kπ+(k∈Z).
(2)令2kπ-≤3ωx+≤2kπ+,则
≤x≤,k∈Z.
故单调递增区间为.
∵f(x)在上单调递增,
∴ (k∈Z).
即解得
∴k=0时,ωmax=.
