江苏省泗洪县2017-2018学年高二上学期期中考试数学试卷
文档属性
| 名称 | 江苏省泗洪县2017-2018学年高二上学期期中考试数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 199.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-30 16:52:58 | ||
图片预览



文档简介
江苏省泗洪县2017—2018学年度第一学期期中考试
高二数学试题
参考公式:
一、填空题:本大题共14小题,每小题5分,共计70分.
1.命题“R,≥”的否定是 .
2.抛物线的焦点坐标是 .
3.双曲线的渐近线方程为_______________.
4.运行如图的程序,则结果为 .
5. 某校共有教师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取1个容量为的样本,已知从女学生中抽取的人数为80人,则____________.
6.如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定的那名运动员的得分的方差为 .
7.经过点,的双曲线的标准方程为________________________________.
8.过点与圆相切的直线方程为____________________________.
9.如果方程表示焦点在轴上的椭圆,那么实数的取值范围是___________.
10.已知点在抛物线上运动,为抛物线的焦点,点的坐标为,则当取得最小值时,点的坐标是__________________________.
11. 在平面直角坐标系中,将圆上点的横坐标保持不变,纵坐标变为原来的倍,所得曲线的方程为_________________.
【试题来源】改编自苏教版选修1-1第29页例2
将圆上点的横坐标保持不变,纵坐标变为原来的一半,求所得曲线的方程,并说明它是什么曲线.
12.若椭圆与直线交于,两点,为的中点,直线(为原点)的斜率为,则的值为______________________.
【试题来源】苏教版选修1-1第61页20题
若椭圆与直线交于,两点,为的中点,直线(为原点)的斜率为,又,求的值.
13.若不等式的解集为区间,且,则_______.
【试题来源】苏教版必修2第129页复习题26题
若直线与曲线恰有一个公共点,则实数的取值范围是__________.
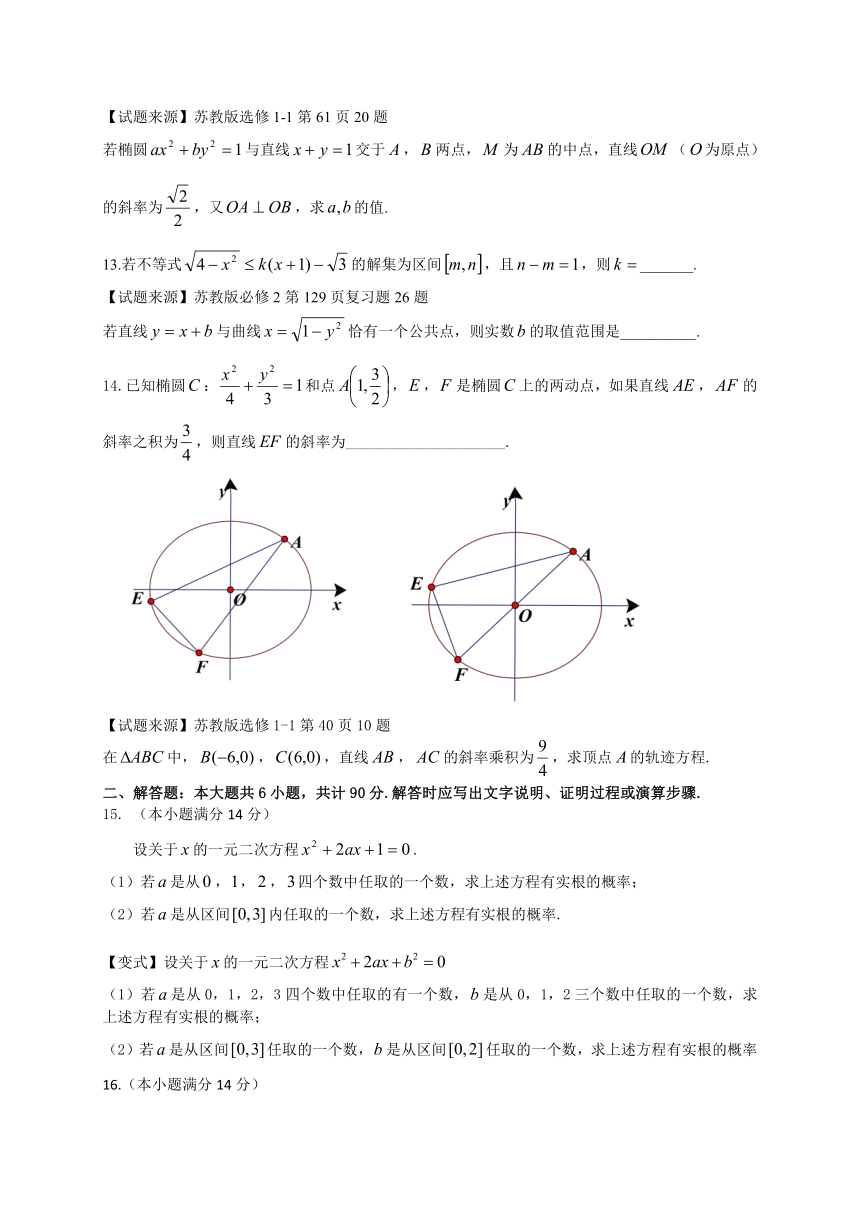
14.已知椭圆:和点,,是椭圆上的两动点,如果直线,的斜率之积为,则直线的斜率为_____________________.
【试题来源】苏教版选修1-1第40页10题
在中,,,直线,的斜率乘积为,求顶点的轨迹方程.
二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤.
15. (本小题满分14分)
设关于的一元二次方程.
(1)若是从,,,四个数中任取的一个数,求上述方程有实根的概率;
(2)若是从区间内任取的一个数,求上述方程有实根的概率.
【变式】设关于的一元二次方程
(1)若是从0,1,2,3四个数中任取的有一个数,是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若是从区间任取的一个数,是从区间任取的一个数,求上述方程有实根的概率
16.(本小题满分14分)
在平面直角坐标系中,已知两定点,,满足的动点所构成的曲线为.
(1)求曲线的方程;
(2)设为曲线上的一个动点,求的取值范围.
【试题来源】苏教版必修2第112页12题
已知点与两个定点,的距离之比为,那么点的坐标应满足什么关系?画出满足条件的点所构成的曲线.
17.(本小题满分14分)
已知命题:,使方程成立;命题:函数在区间
上是减函数.
(1)求使得命题“且”为真命题的的集合;
(2)若“”是“成立”的必要条件,求实数的取值范围.
18.(本小题满分16分)
在平面直角坐标系中,设,分别是椭圆:()的左、右焦点,过点的直线交椭圆于,两点,.
(1)若的周长为,且椭圆的焦距为,求椭圆的方程;
(2)若,求椭圆的离心率.
【试题来源】2014年安徽卷改编
设,分别是椭圆:的左、右焦点,过点的直线交椭圆于两点,
(1)若的周长为16,求;
(2)若,求椭圆的离心率.
19.(本小题满分16分)
在平面直角坐标系中,已知椭圆:(),,分别是椭圆的左、右焦点,是椭圆上任意一点,若的取值范围是.
(1)求椭圆的方程;
(2)若椭圆的左、右顶点分别为,,过点斜率为()的直线交椭圆于,两点,其中点在轴上方.记直线,的斜率分别为,,求证:为定值.
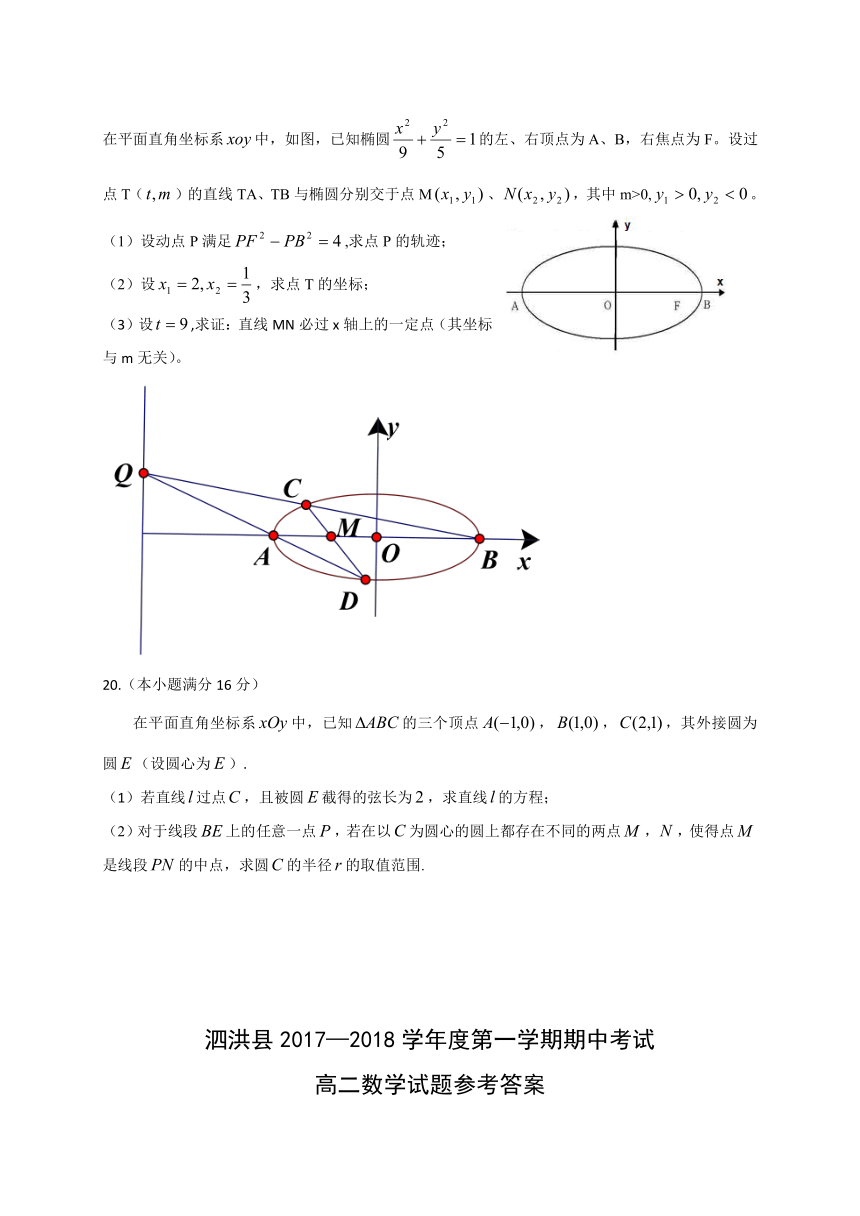
【试题来源】2010江苏卷18题改编
在平面直角坐标系中,如图,已知椭圆的左、右顶点为A、B,右焦点为F。设过点T()的直线TA、TB与椭圆分别交于点M、,其中m>0,。
(1)设动点P满足,求点P的轨迹;
(2)设,求点T的坐标;
(3)设,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
20.(本小题满分16分)
在平面直角坐标系中,已知的三个顶点,,,其外接圆为圆(设圆心为).
(1)若直线过点,且被圆截得的弦长为,求直线的方程;
(2)对于线段上的任意一点,若在以为圆心的圆上都存在不同的两点,,使得点是线段的中点,求圆的半径的取值范围.
泗洪县2017—2018学年度第一学期期中考试
高二数学试题参考答案
一、填空题:本大题共14小题,每小题5分,共计70分.
1., 2.
3. 4.280
5.192 6.
7. 8.
9. 10.
11. 12.
13. 14.
二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤.
15. (本小题满分14分)
解析:设事件为“方程有实根”; -----------------------------1分
当,即或时,方程有实根.-----4分
(1)基本事件共4个:0,1,2,3.事件包含3个基本事件1,2,3,
因为每个基本事件发生的可能性都相同,-----------------------------------6分
所以事件发生的概率.----------------------------------------9分
(2)因为从区间任取一个数的机会是均等的,---------------------------------------11分
所以事件发生的概率.---------------------------------------------------------------14分
16.(本小题满分14分)
解析:设,由得
,----------------------------------------------------------------------------2分
化简得,
所以曲线的方程为.--------------------------------------------------------------6分
(2)设,由为曲线上的一个动点得(*)
-----------------------------8分
由(*)式得,且
代入上式得,又------------------------------------------12分
所以的取值范围为. ---------------------------------------------------------------14分
17.(本小题满分14分)
解:(1)由题意可得,“且”为真即为真且为真
命题为真时,则命题为假,即,方程都不成立,
即, 故;--------------------------------------------------------------------2分
命题为真时,则,即;--------------------------------------------------------------------4分
故集合--------------------------------------------------------------------------------------------6分
(2)“”是“成立”的必要条件,
则的解集是的子集,--------------------------------------8分
当时,不等式解集为?,,符合题意;--------------10分
②当时,则,解得;--------------12分
故的取值范围是或. ---------------------------------------14分
18.(本小题满分16分)
解析:(1)因为的周长为,所以,所以.------------------------------2分
由椭圆的焦距为得,,所以.-------------------------------4分
所以椭圆的方程为.-------------------------------------------------------------------------6分
(2)设(),则,,.--------------8分
由得,
即,解得-----------------------------------------------------10分
所以,------------------------------------------------------------------------------------------------12分
又,所以,所以.
故椭圆的离心率为.------------------------------------------------------------------------------------16分
19.(本小题满分16分)
解析:(1)设为椭圆上任意一点,
所以
因为
所以-----------------------------------2分
因为,所以,-----------------------------------------------4分
所以,所以,,所以,
所以椭圆的方程为.-------------------------------------------------------------------------6分
(2)设直线的方程为(),
由消去得方程,
解得或,所以------------------------------------------8分
同理可以求得----------------------------------------------------------------------10分
又,,三点共线,所以
即,化简得-----------------------------12分
因为点在轴上方,所以,,所以-----------------------------14分
所以,即
故为定值.---------------------------------------------------------------------------------------------------16分
20.(本小题满分16分)
解析:(1)线段的垂直平分线方程为,
线段的垂直平分线方程为.
由得
所以外接圆圆心为,半径为,
所以圆的方程为 . ---------------------------------------------------------------2分
设圆心到直线的距离为,因为直线被圆截得的弦长为,
所以.
当直线垂直于轴时,显然符合题意.即为所求;------------------------------------------4分
当直线不垂直于轴时,设直线的方程为,
则由解得
综上,直线的方程为或.------------------------------------------------------6分
(2)直线的方程为.
设().
因为点是线段的中点,所以,
又都在半径为的圆上,
所以
即-------------------------------------------------------------------8分
因为该关于的方程组有解,即以为圆心,为半径的圆与以为圆心,为半径的圆有公共点.
所以,---------------------------------------10分
又,所以对成立.
而函数在上的值域为,---------------------------------12分
所以,解得.-------------------------------------------------------------------14分
又线段与圆无公共点,
所以对成立,
所以,即,
所以.
故圆的半径的取值范围为.-----------------------------------------------------------16分
高二数学试题
参考公式:
一、填空题:本大题共14小题,每小题5分,共计70分.
1.命题“R,≥”的否定是 .
2.抛物线的焦点坐标是 .
3.双曲线的渐近线方程为_______________.
4.运行如图的程序,则结果为 .
5. 某校共有教师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取1个容量为的样本,已知从女学生中抽取的人数为80人,则____________.
6.如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定的那名运动员的得分的方差为 .
7.经过点,的双曲线的标准方程为________________________________.
8.过点与圆相切的直线方程为____________________________.
9.如果方程表示焦点在轴上的椭圆,那么实数的取值范围是___________.
10.已知点在抛物线上运动,为抛物线的焦点,点的坐标为,则当取得最小值时,点的坐标是__________________________.
11. 在平面直角坐标系中,将圆上点的横坐标保持不变,纵坐标变为原来的倍,所得曲线的方程为_________________.
【试题来源】改编自苏教版选修1-1第29页例2
将圆上点的横坐标保持不变,纵坐标变为原来的一半,求所得曲线的方程,并说明它是什么曲线.
12.若椭圆与直线交于,两点,为的中点,直线(为原点)的斜率为,则的值为______________________.
【试题来源】苏教版选修1-1第61页20题
若椭圆与直线交于,两点,为的中点,直线(为原点)的斜率为,又,求的值.
13.若不等式的解集为区间,且,则_______.
【试题来源】苏教版必修2第129页复习题26题
若直线与曲线恰有一个公共点,则实数的取值范围是__________.
14.已知椭圆:和点,,是椭圆上的两动点,如果直线,的斜率之积为,则直线的斜率为_____________________.
【试题来源】苏教版选修1-1第40页10题
在中,,,直线,的斜率乘积为,求顶点的轨迹方程.
二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤.
15. (本小题满分14分)
设关于的一元二次方程.
(1)若是从,,,四个数中任取的一个数,求上述方程有实根的概率;
(2)若是从区间内任取的一个数,求上述方程有实根的概率.
【变式】设关于的一元二次方程
(1)若是从0,1,2,3四个数中任取的有一个数,是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若是从区间任取的一个数,是从区间任取的一个数,求上述方程有实根的概率
16.(本小题满分14分)
在平面直角坐标系中,已知两定点,,满足的动点所构成的曲线为.
(1)求曲线的方程;
(2)设为曲线上的一个动点,求的取值范围.
【试题来源】苏教版必修2第112页12题
已知点与两个定点,的距离之比为,那么点的坐标应满足什么关系?画出满足条件的点所构成的曲线.
17.(本小题满分14分)
已知命题:,使方程成立;命题:函数在区间
上是减函数.
(1)求使得命题“且”为真命题的的集合;
(2)若“”是“成立”的必要条件,求实数的取值范围.
18.(本小题满分16分)
在平面直角坐标系中,设,分别是椭圆:()的左、右焦点,过点的直线交椭圆于,两点,.
(1)若的周长为,且椭圆的焦距为,求椭圆的方程;
(2)若,求椭圆的离心率.
【试题来源】2014年安徽卷改编
设,分别是椭圆:的左、右焦点,过点的直线交椭圆于两点,
(1)若的周长为16,求;
(2)若,求椭圆的离心率.
19.(本小题满分16分)
在平面直角坐标系中,已知椭圆:(),,分别是椭圆的左、右焦点,是椭圆上任意一点,若的取值范围是.
(1)求椭圆的方程;
(2)若椭圆的左、右顶点分别为,,过点斜率为()的直线交椭圆于,两点,其中点在轴上方.记直线,的斜率分别为,,求证:为定值.
【试题来源】2010江苏卷18题改编
在平面直角坐标系中,如图,已知椭圆的左、右顶点为A、B,右焦点为F。设过点T()的直线TA、TB与椭圆分别交于点M、,其中m>0,。
(1)设动点P满足,求点P的轨迹;
(2)设,求点T的坐标;
(3)设,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
20.(本小题满分16分)
在平面直角坐标系中,已知的三个顶点,,,其外接圆为圆(设圆心为).
(1)若直线过点,且被圆截得的弦长为,求直线的方程;
(2)对于线段上的任意一点,若在以为圆心的圆上都存在不同的两点,,使得点是线段的中点,求圆的半径的取值范围.
泗洪县2017—2018学年度第一学期期中考试
高二数学试题参考答案
一、填空题:本大题共14小题,每小题5分,共计70分.
1., 2.
3. 4.280
5.192 6.
7. 8.
9. 10.
11. 12.
13. 14.
二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤.
15. (本小题满分14分)
解析:设事件为“方程有实根”; -----------------------------1分
当,即或时,方程有实根.-----4分
(1)基本事件共4个:0,1,2,3.事件包含3个基本事件1,2,3,
因为每个基本事件发生的可能性都相同,-----------------------------------6分
所以事件发生的概率.----------------------------------------9分
(2)因为从区间任取一个数的机会是均等的,---------------------------------------11分
所以事件发生的概率.---------------------------------------------------------------14分
16.(本小题满分14分)
解析:设,由得
,----------------------------------------------------------------------------2分
化简得,
所以曲线的方程为.--------------------------------------------------------------6分
(2)设,由为曲线上的一个动点得(*)
-----------------------------8分
由(*)式得,且
代入上式得,又------------------------------------------12分
所以的取值范围为. ---------------------------------------------------------------14分
17.(本小题满分14分)
解:(1)由题意可得,“且”为真即为真且为真
命题为真时,则命题为假,即,方程都不成立,
即, 故;--------------------------------------------------------------------2分
命题为真时,则,即;--------------------------------------------------------------------4分
故集合--------------------------------------------------------------------------------------------6分
(2)“”是“成立”的必要条件,
则的解集是的子集,--------------------------------------8分
当时,不等式解集为?,,符合题意;--------------10分
②当时,则,解得;--------------12分
故的取值范围是或. ---------------------------------------14分
18.(本小题满分16分)
解析:(1)因为的周长为,所以,所以.------------------------------2分
由椭圆的焦距为得,,所以.-------------------------------4分
所以椭圆的方程为.-------------------------------------------------------------------------6分
(2)设(),则,,.--------------8分
由得,
即,解得-----------------------------------------------------10分
所以,------------------------------------------------------------------------------------------------12分
又,所以,所以.
故椭圆的离心率为.------------------------------------------------------------------------------------16分
19.(本小题满分16分)
解析:(1)设为椭圆上任意一点,
所以
因为
所以-----------------------------------2分
因为,所以,-----------------------------------------------4分
所以,所以,,所以,
所以椭圆的方程为.-------------------------------------------------------------------------6分
(2)设直线的方程为(),
由消去得方程,
解得或,所以------------------------------------------8分
同理可以求得----------------------------------------------------------------------10分
又,,三点共线,所以
即,化简得-----------------------------12分
因为点在轴上方,所以,,所以-----------------------------14分
所以,即
故为定值.---------------------------------------------------------------------------------------------------16分
20.(本小题满分16分)
解析:(1)线段的垂直平分线方程为,
线段的垂直平分线方程为.
由得
所以外接圆圆心为,半径为,
所以圆的方程为 . ---------------------------------------------------------------2分
设圆心到直线的距离为,因为直线被圆截得的弦长为,
所以.
当直线垂直于轴时,显然符合题意.即为所求;------------------------------------------4分
当直线不垂直于轴时,设直线的方程为,
则由解得
综上,直线的方程为或.------------------------------------------------------6分
(2)直线的方程为.
设().
因为点是线段的中点,所以,
又都在半径为的圆上,
所以
即-------------------------------------------------------------------8分
因为该关于的方程组有解,即以为圆心,为半径的圆与以为圆心,为半径的圆有公共点.
所以,---------------------------------------10分
又,所以对成立.
而函数在上的值域为,---------------------------------12分
所以,解得.-------------------------------------------------------------------14分
又线段与圆无公共点,
所以对成立,
所以,即,
所以.
故圆的半径的取值范围为.-----------------------------------------------------------16分
同课章节目录
