数学五年级上人教版版5.7实际问题与方程(一)课件(21张)
文档属性
| 名称 | 数学五年级上人教版版5.7实际问题与方程(一)课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-01 13:52:59 | ||
图片预览






文档简介
(共21张PPT)
简易方程
实际问题与方程
(例1 )
(2)老师的岁数比周佳的岁数大15岁。
1.解下列方程。
y-34=71
3+ x=14
2.根据下面叙述说说等量关系。
知识回顾
(1)我们班女生比男生多36人。
男生人数+女生比男生多的人数=女生人数
周佳的岁数+老师比周佳大的岁数=老师的岁数
学习目标
1、我们要学会在实际问题中找等量关系,依据等量关系列方程。
2、我们一起经历用线段图分析解决问题的过程,并归纳出列方程解决实际问题的一般步骤。
3、我们要学会用数学的眼光看待生活中的问题。
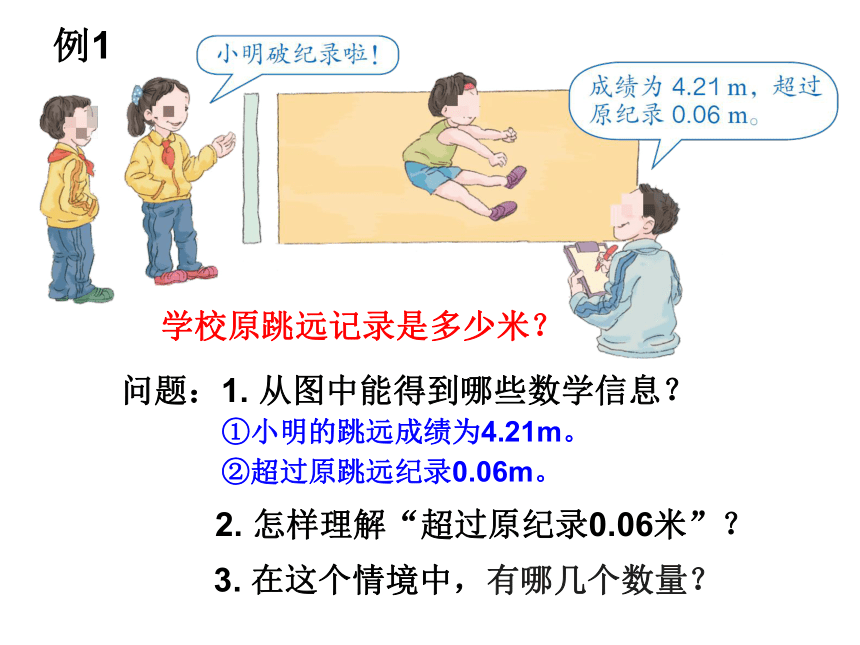
问题:1. 从图中能得到哪些数学信息?
2. 怎样理解“超过原纪录0.06米”?
3. 在这个情境中,有哪几个数量?
例1
学校原跳远记录是多少米?
①小明的跳远成绩为4.21m。
②超过原跳远纪录0.06m。
刚说的数量之间有哪些等量关系呢?
例1
学校原跳远记录是多少米?
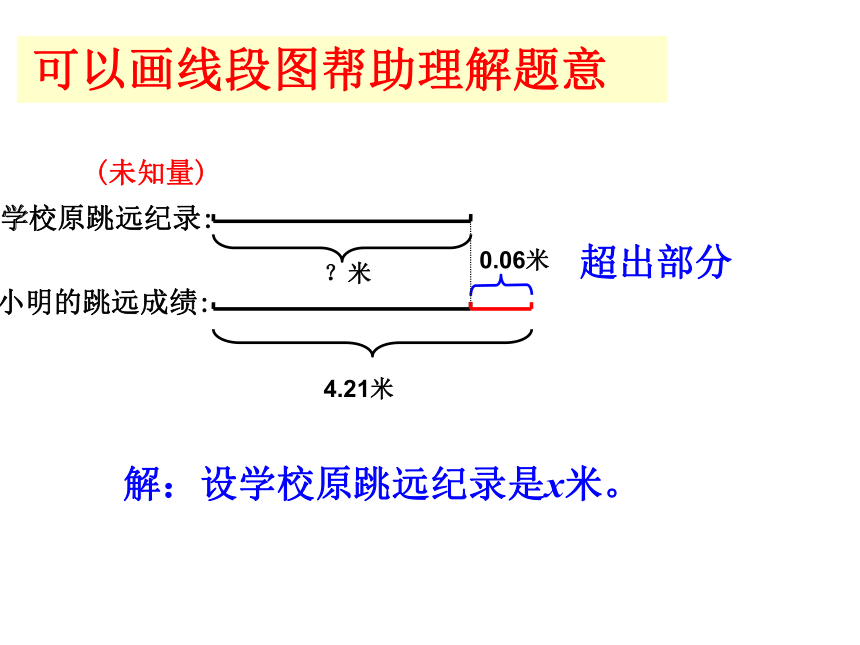
4.21米
0.06米
?米
学校原跳远纪录:
小明的跳远成绩:
可以画线段图帮助理解题意
超出部分
(未知量)
解:设学校原跳远纪录是x米。
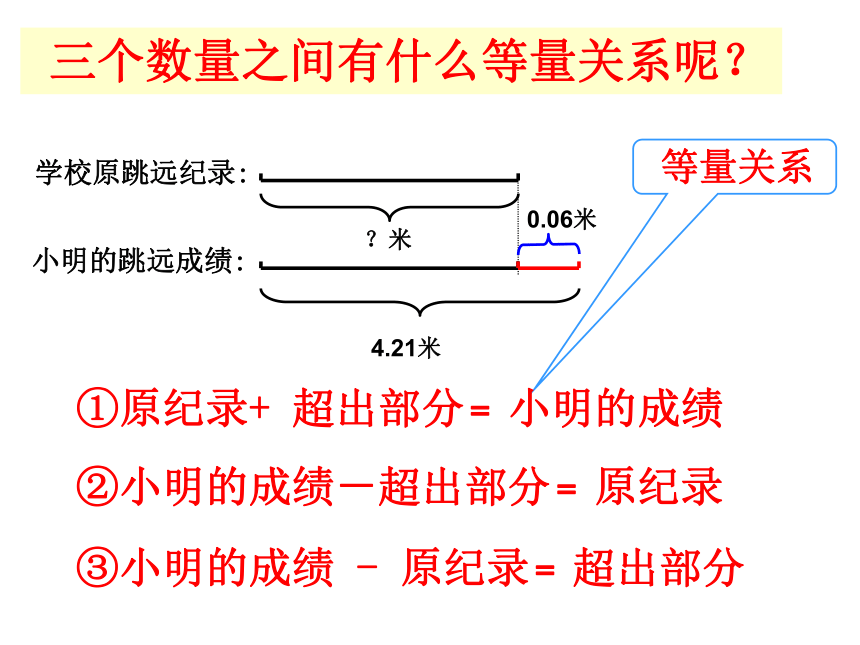
三个数量之间有什么等量关系呢?
②小明的成绩-超出部分﹦原纪录
?米
4.21米
0.06米
学校原跳远纪录:
小明的跳远成绩:
等量关系
③小明的成绩 - 原纪录﹦超出部分
①原纪录+ 超出部分﹦小明的成绩
根据等量关系怎么列式呢?
例1
学校原跳远记录是多少米?
②小明的成绩-超出部分﹦原纪录
4.21- 0.06= x
4.21-0.06=4.15(m)
算术解法:
①原纪录+ 超出部分﹦ 小明的成绩
③小明的成绩 - 原纪录﹦超出部分
x +0.06 = 4.12
4.21- x =0.06
方程解法:
解:设学校原跳远纪录是x米。
答:学校原跳远纪录是4.15米。
原纪录+ 超出部分﹦小明的成绩
x+0.06-0.06=4.21-0.06
x=4.15
你发现什么?
x +0.06 = 4.12
注意:先检验再作答
用方程的思路解决问题,你认为关键是什么?
同一个问题,我们用了几种不同的方法解决?都合理吗?
可以用算术的方法,也可以列方程解答。
找出等量关系
方程解法与算术解法有什么区别
列方程解决问题时,未知数用字母表示,参与列式;算术方法中未知数不参与列式。
小组讨论:列方程解决问题有哪几个步骤?
要求:
1、每个同学至少说出一条,向组长汇报;
2、小组成员在小组内交流讨论;
3、组长收集完整结论后,代表小组向全班汇报。
列方程解决问题的一般步骤:
1、找出未知量,用字母 x 表示;
2.分析实际问题中的数量关系,找出等量关系。
3、根据等量关系列方程;
4、解方程;
5、检验作答。
做一做
问题:你能用方程解决这个问题吗?
写出数量关系,列方程解答。
(1)
小明去年身高多少?
解决这个问题时,注意什么呢?
(注意统一单位)
解:设小明去年身高x米。
0.08+x=1.53
0.08+x-0.08=1.53-0.08
x=1.45
答:小明去年身高1.45米。
8cm=0.08m
方法1:
解:设小明去年身高x米。
8cm=0.08m
方法2:
1.53-x=0.08
1.53-x+x=0.08+x
1.53=0.08+x
0.08+x=1.53
0.08+x-0.08=1.53-0.08
x=1.45
去年的身高+长高的部分=今年的身高
今年的身高-去年的身高=长高的部分
做一做
问题:你能用方程解决这个问题吗?自己试着做一做。
2.
绿色圃中小学教育网http://www.lspjy.com
绿色圃中小学教育网http://www.lspjy.com
(2)
解:设一个滴水的水龙头每分钟浪费x千克水。
x=0.06
答:一个滴水的水龙头每分钟浪费0.06千克水。
半小时=30分钟
30x=1.8
每分钟滴的水×30分钟=半小时滴的水
30x÷30=1.8÷30
提倡节约
反对浪费
课堂小结
今天你有什么收获?
列方程解决问题的一般步骤:
1、找出未知数,用字母 x 表示;
2.分析实际问题中的数量关系,找出等量关系。
3、根据等量关系列方程;
4、解方程;
5、检验作答。
简易方程
实际问题与方程
(例1 )
(2)老师的岁数比周佳的岁数大15岁。
1.解下列方程。
y-34=71
3+ x=14
2.根据下面叙述说说等量关系。
知识回顾
(1)我们班女生比男生多36人。
男生人数+女生比男生多的人数=女生人数
周佳的岁数+老师比周佳大的岁数=老师的岁数
学习目标
1、我们要学会在实际问题中找等量关系,依据等量关系列方程。
2、我们一起经历用线段图分析解决问题的过程,并归纳出列方程解决实际问题的一般步骤。
3、我们要学会用数学的眼光看待生活中的问题。
问题:1. 从图中能得到哪些数学信息?
2. 怎样理解“超过原纪录0.06米”?
3. 在这个情境中,有哪几个数量?
例1
学校原跳远记录是多少米?
①小明的跳远成绩为4.21m。
②超过原跳远纪录0.06m。
刚说的数量之间有哪些等量关系呢?
例1
学校原跳远记录是多少米?
4.21米
0.06米
?米
学校原跳远纪录:
小明的跳远成绩:
可以画线段图帮助理解题意
超出部分
(未知量)
解:设学校原跳远纪录是x米。
三个数量之间有什么等量关系呢?
②小明的成绩-超出部分﹦原纪录
?米
4.21米
0.06米
学校原跳远纪录:
小明的跳远成绩:
等量关系
③小明的成绩 - 原纪录﹦超出部分
①原纪录+ 超出部分﹦小明的成绩
根据等量关系怎么列式呢?
例1
学校原跳远记录是多少米?
②小明的成绩-超出部分﹦原纪录
4.21- 0.06= x
4.21-0.06=4.15(m)
算术解法:
①原纪录+ 超出部分﹦ 小明的成绩
③小明的成绩 - 原纪录﹦超出部分
x +0.06 = 4.12
4.21- x =0.06
方程解法:
解:设学校原跳远纪录是x米。
答:学校原跳远纪录是4.15米。
原纪录+ 超出部分﹦小明的成绩
x+0.06-0.06=4.21-0.06
x=4.15
你发现什么?
x +0.06 = 4.12
注意:先检验再作答
用方程的思路解决问题,你认为关键是什么?
同一个问题,我们用了几种不同的方法解决?都合理吗?
可以用算术的方法,也可以列方程解答。
找出等量关系
方程解法与算术解法有什么区别
列方程解决问题时,未知数用字母表示,参与列式;算术方法中未知数不参与列式。
小组讨论:列方程解决问题有哪几个步骤?
要求:
1、每个同学至少说出一条,向组长汇报;
2、小组成员在小组内交流讨论;
3、组长收集完整结论后,代表小组向全班汇报。
列方程解决问题的一般步骤:
1、找出未知量,用字母 x 表示;
2.分析实际问题中的数量关系,找出等量关系。
3、根据等量关系列方程;
4、解方程;
5、检验作答。
做一做
问题:你能用方程解决这个问题吗?
写出数量关系,列方程解答。
(1)
小明去年身高多少?
解决这个问题时,注意什么呢?
(注意统一单位)
解:设小明去年身高x米。
0.08+x=1.53
0.08+x-0.08=1.53-0.08
x=1.45
答:小明去年身高1.45米。
8cm=0.08m
方法1:
解:设小明去年身高x米。
8cm=0.08m
方法2:
1.53-x=0.08
1.53-x+x=0.08+x
1.53=0.08+x
0.08+x=1.53
0.08+x-0.08=1.53-0.08
x=1.45
去年的身高+长高的部分=今年的身高
今年的身高-去年的身高=长高的部分
做一做
问题:你能用方程解决这个问题吗?自己试着做一做。
2.
绿色圃中小学教育网http://www.lspjy.com
绿色圃中小学教育网http://www.lspjy.com
(2)
解:设一个滴水的水龙头每分钟浪费x千克水。
x=0.06
答:一个滴水的水龙头每分钟浪费0.06千克水。
半小时=30分钟
30x=1.8
每分钟滴的水×30分钟=半小时滴的水
30x÷30=1.8÷30
提倡节约
反对浪费
课堂小结
今天你有什么收获?
列方程解决问题的一般步骤:
1、找出未知数,用字母 x 表示;
2.分析实际问题中的数量关系,找出等量关系。
3、根据等量关系列方程;
4、解方程;
5、检验作答。
