2.8 圆锥的侧面积 同步练习(含简略答案)
文档属性
| 名称 | 2.8 圆锥的侧面积 同步练习(含简略答案) |  | |
| 格式 | zip | ||
| 文件大小 | 106.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-04 22:24:31 | ||
图片预览

文档简介
第2章 对称图形——圆
2.8 圆锥的侧面积
【基础提优】
1.将圆心角为90°,面积为4π cm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面圆的半径为( )21教育网
A.1 cm B.2 cm C.3 cm D.4 cm
2.如图,圆锥形冰淇淋盒的母线长是13 cm,高是12 cm,则该圆锥底面圆的面积是( )
A.10π cm2 B.25π cm2 C.60π cm2 D.65π cm2
(第2题) (第3题)
3.如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角的度数为( )www.21-cn-jy.com
A.288° B.144° C.216° D.120°
4.若一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的扇形的圆心角的度数为( )
A.120° B.180° C.240° D.300°
5.若一个圆锥的底面积为4π cm2,高为4 cm,则该圆锥的侧面展开图的扇形的圆心角的度数为( )2·1·c·n·j·y
A.40° B.80° C.120° D.150°
6.如图,从一个直径为4 cm的圆形铁皮中剪出一个圆心角为60°的扇形ABC,并将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 cm.
(第6题) (第7题)
7.如图,已知⊙O的半径为4,∠A=45°,若一个圆锥的侧面展开图与扇形OBC能完全重合,则该圆锥的底面圆的半径为 .【来源:21·世纪·教育·网】
8.已知一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为 (结果保留π).21·世纪*教育网
9.用半径为10 cm,圆心角为216°的扇形做成一个圆锥的侧面,求这个圆锥的高.
【拓展提优】
1.已知Rt△ABC的一条直角边AB=12 cm,另一条直角边BC=5 cm,则以AB为轴旋转一周,所得到的圆锥的表面积是( )21世纪教育网版权所有
A.90π cm2 B.290π cm2 C.155π cm2 D.65π cm2
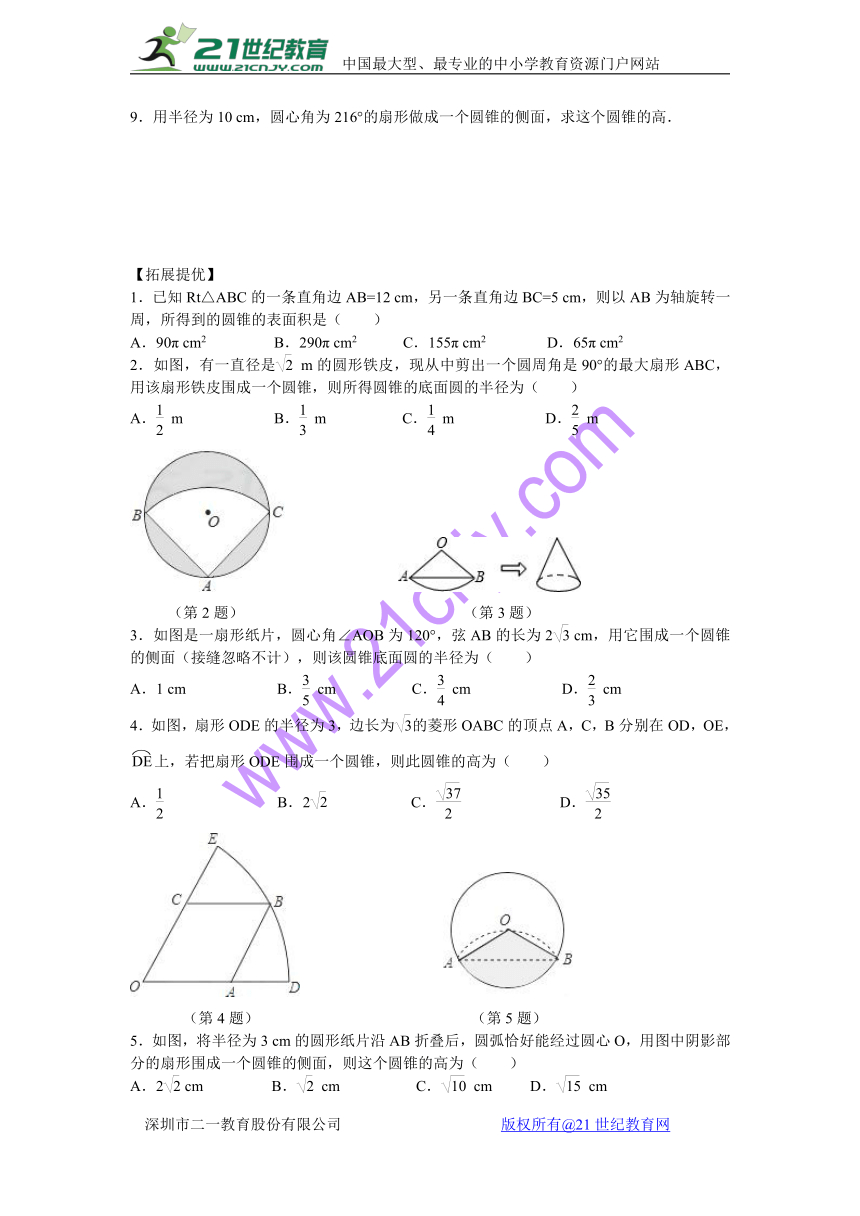
2.如图,有一直径是 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
A. m B. m C. m D. m
(第2题) (第3题)
3.如图是一扇形纸片,圆心角∠AOB为120°,弦AB的长为2 cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )21cnjy.com
A.1 cm B. cm C. cm D. cm
4.如图,扇形ODE的半径为3,边长为的菱形OABC的顶点A,C,B分别在OD,OE, 上,若把扇形ODE围成一个圆锥,则此圆锥的高为( )21·cn·jy·com
A. B.2 C. D.
(第4题) (第5题)
5.如图,将半径为3 cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )www-2-1-cnjy-com
A.2 cm B. cm C. cm D. cm
6.从纸上剪下一个圆和一个扇形的纸片(如图),圆的半径为2,扇形的圆心角等于120°.如果用它们恰好能围成一个圆锥模型,那么此扇形的半径为 .
(第6题) (第7题)
7.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为 cm2.
8.如图,如果从半径为5cm的圆形纸片上剪去 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是 cm.2-1-c-n-j-y
(第8题)
9.如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到点A,求这根绳子的最短长度.
参考答案
【基础提优】
1-5 ABABC
6.1
7.1
8.68π
9.8 cm
【拓展提优】
1-5 ACDDA
6.6
7.2π
8.3
9.(1)4;120° (2)6
2.8 圆锥的侧面积
【基础提优】
1.将圆心角为90°,面积为4π cm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面圆的半径为( )21教育网
A.1 cm B.2 cm C.3 cm D.4 cm
2.如图,圆锥形冰淇淋盒的母线长是13 cm,高是12 cm,则该圆锥底面圆的面积是( )
A.10π cm2 B.25π cm2 C.60π cm2 D.65π cm2
(第2题) (第3题)
3.如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角的度数为( )www.21-cn-jy.com
A.288° B.144° C.216° D.120°
4.若一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的扇形的圆心角的度数为( )
A.120° B.180° C.240° D.300°
5.若一个圆锥的底面积为4π cm2,高为4 cm,则该圆锥的侧面展开图的扇形的圆心角的度数为( )2·1·c·n·j·y
A.40° B.80° C.120° D.150°
6.如图,从一个直径为4 cm的圆形铁皮中剪出一个圆心角为60°的扇形ABC,并将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 cm.
(第6题) (第7题)
7.如图,已知⊙O的半径为4,∠A=45°,若一个圆锥的侧面展开图与扇形OBC能完全重合,则该圆锥的底面圆的半径为 .【来源:21·世纪·教育·网】
8.已知一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为 (结果保留π).21·世纪*教育网
9.用半径为10 cm,圆心角为216°的扇形做成一个圆锥的侧面,求这个圆锥的高.
【拓展提优】
1.已知Rt△ABC的一条直角边AB=12 cm,另一条直角边BC=5 cm,则以AB为轴旋转一周,所得到的圆锥的表面积是( )21世纪教育网版权所有
A.90π cm2 B.290π cm2 C.155π cm2 D.65π cm2
2.如图,有一直径是 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
A. m B. m C. m D. m
(第2题) (第3题)
3.如图是一扇形纸片,圆心角∠AOB为120°,弦AB的长为2 cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )21cnjy.com
A.1 cm B. cm C. cm D. cm
4.如图,扇形ODE的半径为3,边长为的菱形OABC的顶点A,C,B分别在OD,OE, 上,若把扇形ODE围成一个圆锥,则此圆锥的高为( )21·cn·jy·com
A. B.2 C. D.
(第4题) (第5题)
5.如图,将半径为3 cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )www-2-1-cnjy-com
A.2 cm B. cm C. cm D. cm
6.从纸上剪下一个圆和一个扇形的纸片(如图),圆的半径为2,扇形的圆心角等于120°.如果用它们恰好能围成一个圆锥模型,那么此扇形的半径为 .
(第6题) (第7题)
7.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为 cm2.
8.如图,如果从半径为5cm的圆形纸片上剪去 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是 cm.2-1-c-n-j-y
(第8题)
9.如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到点A,求这根绳子的最短长度.
参考答案
【基础提优】
1-5 ABABC
6.1
7.1
8.68π
9.8 cm
【拓展提优】
1-5 ACDDA
6.6
7.2π
8.3
9.(1)4;120° (2)6
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
