14.3.1 因式分解概念与提公因式(2课时打包)
文档属性
| 名称 | 14.3.1 因式分解概念与提公因式(2课时打包) |

|
|
| 格式 | zip | ||
| 文件大小 | 546.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-02 00:00:00 | ||
图片预览











文档简介
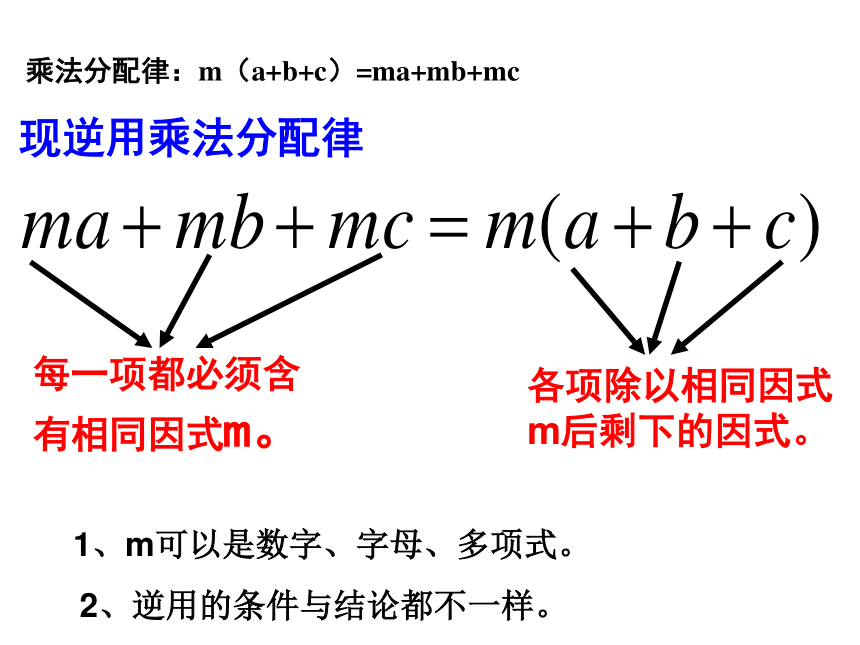
课件55张PPT。分析下列计算是整式乘法中的哪一种并求出结果: (口答)温故知新(1)(2)(3)乘法分配律:m(a+b+c)=ma+mb+mc每一项都必须含有相同因式m。现逆用乘法分配律各项除以相同因式
m后剩下的因式。1、m可以是数字、字母、多项式。2、逆用的条件与结论都不一样。定义 一般地,把一个多项式转化成几个整式的积的形式,叫做因式分解,有时我们也把这一过程叫做分解因式。想一想:分解因式与整式乘法有何关系注意:1.因式分解不是运算,是一种多项式的变形;
因式分解与多项式乘法互为逆变形。2.因式分解必须在整式范围内进行,否则不属于因式分解;3.利用整式的乘法可以验证因式分解是否正确.想一想: 分解因式与整式乘法有何关系?分解因式与整式乘法是互逆过程几个整式的积
m(a+b+c)一个多项式
ma+mb+mc 整式乘法因式分解练习一.下列由左边到右边的变形,哪些是因式分解?哪些不是?为什么?
1)x 2 –y 2+1=(x +y )(x -y )+1
2)6x2y3=3xy·2xy2
3) (不是)(不是)(不是)是不是是不是不是不是不是下列代数式从左到右的变形是因式分解吗?探索新知公因式的定义:
一个多项式各项都含有的相同因式, 叫做这个多项式各项的公因式. 多项式中各项都含有的相同因式,叫做这个多项式各项的公因式。 怎样确定多项式的公因式?
公因式与多项式的各项有什么关系?公因式:
1、找出下列多项式中各项中含有的相同因式.探索新知正确找出多项式各项公因式的关键是:1、定系数:公因式的系数是多项式各项系数的最大公约数。
2、定字母: 字母取多项式各项中都含有的相同的字母。 3、定指数: 相同字母的指数取各项中最小的一个,即字母最低次幂
说出下列各多项式的公因式:
(1)ma + mb ;
(2)4kx - 8ky ;
(3)5y3+20y2 ;
(4)a2b-2ab2+ab .m4k5y2ab一定系数 二定字母 三定指数找一找: 下列各多项式的公因式是什么? (3)(a)(a2)(2(m+n))(3mn)(-2xy)(1) 3x+6y
(2)ab-2ac
(3) a 2 - a 3
(4)4 (m+n) 2 +2(m+n)
(5)9 m 2n-6mn
(6)-6 x 2 y-8 xy 2 ? 7x2 -21x
? 8 a 3 b2 –12ab 3 + ab
? m b2 + n b
? 7x 3y2 –42x2y 3
? 4a2 b – 2a b2 + 6abc说出下列各式的公因式:
7xabb7x2y22ab 指出下列各多项式中各项的公因式
⑴ax+ay-a ( )
⑵5x2y3-10x2y ( )
⑶24abc-9a2b2 ( )
⑷m2n+mn2 ( )
⑸x(x-y)2-y(x-y) ( )独立练习 巩固新知a5x2y3abmnx-y 如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式.这种分解因式的方法叫做提公因式法.概念引入:因式分解:把公因式提出来,多项式ma+mb+mc 就可以分解成两个因式m和(a+b+c)的乘积。像这种因式分解的方法,叫做提取公因式法。解:公因式多项式中各项都含有的相同因式,称之为公因式提公因式法热身运动1.填空:(口答)(1)(2)(3)(4) 例1 把 9x2– 6xy+3xz 分解因式.=3x·3x - 3x·2y + 3x·z 解:=3x (3x-2y+z)9x2 – 6 x y + 3x z 方法步骤:
①找出 — 公因式;
②提出 — 公因式,
(即用多项式中每一项除以公因式)例2: 分解因式
8a3b-12ab3c+ab解: 原式=ab·8a2-ab·12b2c+ab·1
=ab(8a2-12b2c+1)判断下列分解因式正确吗
2x2+3x3+x=x(2x+3x2)
3a2c-6a3c=3a2(c-2ac)X(2X+3X2+1)3a2c(1-2a)注意: 提取公因式后: (1)另一个因式不能再含 有公因式(2)另一个因式的项数与原多项式的项数一致不要漏掉1如果多项式的某一项正好是公因式,要注意该项在提取了公因式后,应该用“1”顶替它原来的位置,切不可把“1”漏掉。例3. 把 -24x3 –12x2 +28x 分解因式.当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
解:原式==提负号
要变号(24x3÷4x+12x2÷4x-28x÷4x)(6x2+3x-7)=练习. 将下列各式分解因式:? 25x-5
? 3 x3 - 3x2 –9x
? 8a 2c+ 2b c
? - 4a 3b3 + 6 a2 b - 2ab
? - 2x2 –12xy2 +8xy3 练习 把下列各式分解因式:
a提公因式法分解因式正确的找出多项式各项的公因式。注意:1 多项式是几项,提公因式后也剩几项。
2 当多项式的某一项和公因式相同时提公因 式后剩余的项是1。
3、当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
怎样正确多项式各项的公因式? 1、公因式的系数是多项式各项系 数的最大公约数; 字母:2、字母取多项式各项中都含有的相同的字母; 指数:3、相同字母的指数取各项中最小的一个,即字母最低次幂; 注: 多项式各项的公因式可以是单项式,也可以是多项式 。 系数:2.把下列各式分解因式:(1)(2)(3)牛刀小试练习二:分解因式
–a2+ab-ac
-2x3+4x2+2x=?a(a?b+c)=?2x(x2?2x?1)例4:把2a(b+c)-5(b+c)分解因式 (b+c)(b+c)解: 2a(b+c)-5(b+c)
= (b+c)(2a-5) 注意:公因式可以是数字,字母,也 可以是单项式,还可以是多项式。练习三、把下列各式分解因式:
(1)x(a+b)+y(a+b)
(2)3a(x-y)-(x-y)
(3)6(p+q)2-12(p+q)解:(1)原式=(a+b)(x+ y)
(2)原式=(x-y)(3a-1)
(3)原式=6(p+q)(p+q-2)确定公因式要对数字因数和字母分别进行考虑:
1.各项系数都是整数时,公因式的系数应取各项系数的最大公约数;
2.字母取各项相同的字母,而且各字母的指数取次数最低的华山论剑4. 把下列各式分解因式:(1)ax+xy=( )( )(2)3mx-6my =( )( )(3)x2y+xy2=( )( )(4)15a2+10a=( )( )(5)12xyz-9x2y2=( )( )x 3m xy5a3a+23xy4z-3xy将下列多项式因式分解:a+yx-2yx+y(6) 2a(b+c)-3(b+c)=( )( )b+c 2a-3小结:本节课我们学习了哪些知识?3、确定公因式的方法 (1)系数——取各项的最大公约数
(2)字母——取各项相同字母
(3)指数——取各项相同字母的最低次幂4、提公因式法分解因式的步骤(1)确定公因式
(2)用公因式去除多项式的各项得另一因式
(3)写成这两个因式的积的形式1、什么叫做公因式?2、什么叫提公因式法?2、确定公因式的方法:小结3、提公因式法分解因式步骤(分两步):1、什么叫因式分解?(1)定系数 (2)定字母 (3)定指数第一步,找出公因式;
第二步,提取公因式.4、提公因式法分解因式应注意的问题:(1)公因式要提尽;(2)小心漏掉1;(3)提出负号时,要注意变号.1、确定公因式的方法:
(1)公因式的系数是多项式各项系数的最大公约数。 (2)字母取多项式各项中都含有的相同的字母。 (3)相同字母的指数取各项中最小的一个,即最低次幂。小结2、提公因式法分解因式:
第一步,找出公因式;
第二步,提公因式,即用多项式除以公因式.再见教学过程:一、复习提问:1、把 化成 的形式,叫做把这个多项式因式分解。2、因式分解与 是互逆变形,分解的结果对不对可以用 运算检验 一个多项式
几个整式的乘积 整式乘法
整式乘法回顾与思考 1 多项式的分解因式的概念:
把一个多项式化为几个整式乘积的形式,叫做把这个多项式分解因式.
2 分解因式与整式乘法是互逆过程.
3 分解因式要注意以下几点:
① 分解的对象必须是多项式.
② 分解的结果一定是几个整式的乘积的形式.
? a c+ b c
? 3 x2 +x
? 30 m b2 + 5n b
? 3x+6
? a2 b – 2a b2 + ab
? 7 ( a– 3 ) – b ( a– 3)下列各多项式有没有共同的因式?c x5b3aba-3提取公因式法1、 中各项的公因式是
__________。公因式:一个多项式每一项都含有的相同的因式,叫做这个多项式各项的公因式。3xy2找公因式的方法:1:系数为 ;
2、字母是 ;
3、字母的次数 。各系数的最小公倍数相同字母相同字母的最低次数练习:①5x2-25x的公因式为 ;
②-2ab2+4a2b3的公因式为 ,
③多项式x2-1与(x-1)2的公因式是 。5x-2ab2x-1如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成乘积的形式。这种分解因式的方法叫做提公因式法。提取公因式法练习:
1、把多项式m2(a-2)+m(2-a)分解因式等于( )
A.(a-2)(m2+m) B.(a-2)(m2-m)
C.m(a-2)(m-1) D.m(a-2)(m+1)C例1、把下列多项式因式分解:
①25x2y3-15x2y2 ②9a(a-b)2-15(b-a)3
③8xmyn-1-12x3myn ④mn(m-n)-n(n-m)2
⑤(b-a)2-2a+2b ⑥a(x-a)(x+y)2-b(x-a)2(x+y)
例2、把下列多项式因式分解:
①6a3b2-3a2b3-18a2b3
②-4x2yz-12xy3z+4xyz
③m(1-x)-n(x-1)+p(1-x)
④-ab(a-b)2+a(b-a)2-a(a-b)2
例3、把下列多项式因式分解:
①m2-mn+mx-nx ②am+bm+an+bn+a+b
③a2b2-a2-b2+1 ④10a2x+21xy2-14ax2-15ay2
⑤2x2(-2x+9)-28x ⑥m2-mn+5n-5m(用两种方法) 1、分解因式计算 (-2)101+(-2)100
2、利用简便方法计算:
4.3x199.8+0.76x1998-1.9x199.8
3、已知 a+b=3, ab=2,
求代数式 a2 b + 2 a2 b2 +a b2 的值。
4、把 9am+1 –21 am+7a m-1分解因式
5、解方程.(x-4)2-(4-x)(8-x)=12
6、化简:1+x+x(1+x)+x(1+x)2+...+x(1+x)2015例4、分解因式的应用(1) 13.8×0.125+86.2×1/8(2)已知a+b=5,ab=3,求a2b+ab2的值. 解:原式=13.8×0.125+86.2×0.125
=0.125×(13.8+86.2)
=0.125×100
=12.5 解: a2b+ab2 =ab(a+b)=3 × 5=15因式分解应用
拓展运用:6.已知1+x+x2+x3=0.
求x+x2+x3+x4+……+x2015的值.解:原式=x(1+x+x2+x3) +x5(1+x+x2+x3) +……+ x2012(1+x+x2+x3)
= 0
6、分解因式:①4xmynb-6xm+1yn+2+2xm+2yn+1②a(x+y-z) -b(z-x-y) -c(x-z+y)③(5x-2y)2 +(2x+5y)2解:原式=2xmyn(2b-3xy2+x2y)解:原式=(x+y-z)(a+b-c)解:原式=25x2-20xy+4y2+4x2+20xy+25y2
=29x2+29y2
=29(x2+y2)3.试说明:817-279-913能被45整除.解:∵原式=(34)7- (33)9- (32)13
=328-327-326
=326(32-3-1)
=326×5
=325×45
∴817-279-913能被45整除.(1)(2)(3) 1993-199能被200整除吗?还能被哪些整数整除?谢谢 再见作业1、把下列多项式因式分解:
①6(x-2)+x(2-x) ②24a(a-b)2+18(b-a)2
③(x-y)2-(y-x)3 ④(m+1)(m-1)+(m-1)
⑤(a-3)2-2a+6 ⑥15x(a-b)2-3y(b-a)
⑦ -4a3+4a2-16a ⑧2x3+x2-6x-3 (用两种方法) 作业2、把下列多项式因式分解:
①-1/5abc+1/5ab2-a2bc ②2x(x-y)2-4x2(y-x)2
③(x-y)3-2z(y-x)2 ④(m-n)4-m(n-m)3+n(n-m)3
⑤3x(a+2b)-6xy(2b+a) ⑥7x2-3y+xy-21x(用两种方法) 作业3、把下列多项式因式分解:
①xyz2-xy2z+x2yz ②(b-a)2-2a+2b
③(2a+b)(3a-2b)-4a(2a+b) ④5(x-Y)3+10(y-x)2
⑤15x(a-b)2-3y(b-a)2 ⑥4a2+2ab+6a+3b(用两种方法) 作业4、把下列多项式因式分解:
①3ax+4ay+3bx+4by ②-2xy-4x2y+8y3y
③-3x2+12x3-3x ④-4a2-6ab-2a
⑤-8(a-b)3-4(a-b)2+2(a-b)⑥2ax-10ay+5by-bx(用两种方法)
m后剩下的因式。1、m可以是数字、字母、多项式。2、逆用的条件与结论都不一样。定义 一般地,把一个多项式转化成几个整式的积的形式,叫做因式分解,有时我们也把这一过程叫做分解因式。想一想:分解因式与整式乘法有何关系注意:1.因式分解不是运算,是一种多项式的变形;
因式分解与多项式乘法互为逆变形。2.因式分解必须在整式范围内进行,否则不属于因式分解;3.利用整式的乘法可以验证因式分解是否正确.想一想: 分解因式与整式乘法有何关系?分解因式与整式乘法是互逆过程几个整式的积
m(a+b+c)一个多项式
ma+mb+mc 整式乘法因式分解练习一.下列由左边到右边的变形,哪些是因式分解?哪些不是?为什么?
1)x 2 –y 2+1=(x +y )(x -y )+1
2)6x2y3=3xy·2xy2
3) (不是)(不是)(不是)是不是是不是不是不是不是下列代数式从左到右的变形是因式分解吗?探索新知公因式的定义:
一个多项式各项都含有的相同因式, 叫做这个多项式各项的公因式. 多项式中各项都含有的相同因式,叫做这个多项式各项的公因式。 怎样确定多项式的公因式?
公因式与多项式的各项有什么关系?公因式:
1、找出下列多项式中各项中含有的相同因式.探索新知正确找出多项式各项公因式的关键是:1、定系数:公因式的系数是多项式各项系数的最大公约数。
2、定字母: 字母取多项式各项中都含有的相同的字母。 3、定指数: 相同字母的指数取各项中最小的一个,即字母最低次幂
说出下列各多项式的公因式:
(1)ma + mb ;
(2)4kx - 8ky ;
(3)5y3+20y2 ;
(4)a2b-2ab2+ab .m4k5y2ab一定系数 二定字母 三定指数找一找: 下列各多项式的公因式是什么? (3)(a)(a2)(2(m+n))(3mn)(-2xy)(1) 3x+6y
(2)ab-2ac
(3) a 2 - a 3
(4)4 (m+n) 2 +2(m+n)
(5)9 m 2n-6mn
(6)-6 x 2 y-8 xy 2 ? 7x2 -21x
? 8 a 3 b2 –12ab 3 + ab
? m b2 + n b
? 7x 3y2 –42x2y 3
? 4a2 b – 2a b2 + 6abc说出下列各式的公因式:
7xabb7x2y22ab 指出下列各多项式中各项的公因式
⑴ax+ay-a ( )
⑵5x2y3-10x2y ( )
⑶24abc-9a2b2 ( )
⑷m2n+mn2 ( )
⑸x(x-y)2-y(x-y) ( )独立练习 巩固新知a5x2y3abmnx-y 如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式.这种分解因式的方法叫做提公因式法.概念引入:因式分解:把公因式提出来,多项式ma+mb+mc 就可以分解成两个因式m和(a+b+c)的乘积。像这种因式分解的方法,叫做提取公因式法。解:公因式多项式中各项都含有的相同因式,称之为公因式提公因式法热身运动1.填空:(口答)(1)(2)(3)(4) 例1 把 9x2– 6xy+3xz 分解因式.=3x·3x - 3x·2y + 3x·z 解:=3x (3x-2y+z)9x2 – 6 x y + 3x z 方法步骤:
①找出 — 公因式;
②提出 — 公因式,
(即用多项式中每一项除以公因式)例2: 分解因式
8a3b-12ab3c+ab解: 原式=ab·8a2-ab·12b2c+ab·1
=ab(8a2-12b2c+1)判断下列分解因式正确吗
2x2+3x3+x=x(2x+3x2)
3a2c-6a3c=3a2(c-2ac)X(2X+3X2+1)3a2c(1-2a)注意: 提取公因式后: (1)另一个因式不能再含 有公因式(2)另一个因式的项数与原多项式的项数一致不要漏掉1如果多项式的某一项正好是公因式,要注意该项在提取了公因式后,应该用“1”顶替它原来的位置,切不可把“1”漏掉。例3. 把 -24x3 –12x2 +28x 分解因式.当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
解:原式==提负号
要变号(24x3÷4x+12x2÷4x-28x÷4x)(6x2+3x-7)=练习. 将下列各式分解因式:? 25x-5
? 3 x3 - 3x2 –9x
? 8a 2c+ 2b c
? - 4a 3b3 + 6 a2 b - 2ab
? - 2x2 –12xy2 +8xy3 练习 把下列各式分解因式:
a提公因式法分解因式正确的找出多项式各项的公因式。注意:1 多项式是几项,提公因式后也剩几项。
2 当多项式的某一项和公因式相同时提公因 式后剩余的项是1。
3、当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号。
怎样正确多项式各项的公因式? 1、公因式的系数是多项式各项系 数的最大公约数; 字母:2、字母取多项式各项中都含有的相同的字母; 指数:3、相同字母的指数取各项中最小的一个,即字母最低次幂; 注: 多项式各项的公因式可以是单项式,也可以是多项式 。 系数:2.把下列各式分解因式:(1)(2)(3)牛刀小试练习二:分解因式
–a2+ab-ac
-2x3+4x2+2x=?a(a?b+c)=?2x(x2?2x?1)例4:把2a(b+c)-5(b+c)分解因式 (b+c)(b+c)解: 2a(b+c)-5(b+c)
= (b+c)(2a-5) 注意:公因式可以是数字,字母,也 可以是单项式,还可以是多项式。练习三、把下列各式分解因式:
(1)x(a+b)+y(a+b)
(2)3a(x-y)-(x-y)
(3)6(p+q)2-12(p+q)解:(1)原式=(a+b)(x+ y)
(2)原式=(x-y)(3a-1)
(3)原式=6(p+q)(p+q-2)确定公因式要对数字因数和字母分别进行考虑:
1.各项系数都是整数时,公因式的系数应取各项系数的最大公约数;
2.字母取各项相同的字母,而且各字母的指数取次数最低的华山论剑4. 把下列各式分解因式:(1)ax+xy=( )( )(2)3mx-6my =( )( )(3)x2y+xy2=( )( )(4)15a2+10a=( )( )(5)12xyz-9x2y2=( )( )x 3m xy5a3a+23xy4z-3xy将下列多项式因式分解:a+yx-2yx+y(6) 2a(b+c)-3(b+c)=( )( )b+c 2a-3小结:本节课我们学习了哪些知识?3、确定公因式的方法 (1)系数——取各项的最大公约数
(2)字母——取各项相同字母
(3)指数——取各项相同字母的最低次幂4、提公因式法分解因式的步骤(1)确定公因式
(2)用公因式去除多项式的各项得另一因式
(3)写成这两个因式的积的形式1、什么叫做公因式?2、什么叫提公因式法?2、确定公因式的方法:小结3、提公因式法分解因式步骤(分两步):1、什么叫因式分解?(1)定系数 (2)定字母 (3)定指数第一步,找出公因式;
第二步,提取公因式.4、提公因式法分解因式应注意的问题:(1)公因式要提尽;(2)小心漏掉1;(3)提出负号时,要注意变号.1、确定公因式的方法:
(1)公因式的系数是多项式各项系数的最大公约数。 (2)字母取多项式各项中都含有的相同的字母。 (3)相同字母的指数取各项中最小的一个,即最低次幂。小结2、提公因式法分解因式:
第一步,找出公因式;
第二步,提公因式,即用多项式除以公因式.再见教学过程:一、复习提问:1、把 化成 的形式,叫做把这个多项式因式分解。2、因式分解与 是互逆变形,分解的结果对不对可以用 运算检验 一个多项式
几个整式的乘积 整式乘法
整式乘法回顾与思考 1 多项式的分解因式的概念:
把一个多项式化为几个整式乘积的形式,叫做把这个多项式分解因式.
2 分解因式与整式乘法是互逆过程.
3 分解因式要注意以下几点:
① 分解的对象必须是多项式.
② 分解的结果一定是几个整式的乘积的形式.
? a c+ b c
? 3 x2 +x
? 30 m b2 + 5n b
? 3x+6
? a2 b – 2a b2 + ab
? 7 ( a– 3 ) – b ( a– 3)下列各多项式有没有共同的因式?c x5b3aba-3提取公因式法1、 中各项的公因式是
__________。公因式:一个多项式每一项都含有的相同的因式,叫做这个多项式各项的公因式。3xy2找公因式的方法:1:系数为 ;
2、字母是 ;
3、字母的次数 。各系数的最小公倍数相同字母相同字母的最低次数练习:①5x2-25x的公因式为 ;
②-2ab2+4a2b3的公因式为 ,
③多项式x2-1与(x-1)2的公因式是 。5x-2ab2x-1如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成乘积的形式。这种分解因式的方法叫做提公因式法。提取公因式法练习:
1、把多项式m2(a-2)+m(2-a)分解因式等于( )
A.(a-2)(m2+m) B.(a-2)(m2-m)
C.m(a-2)(m-1) D.m(a-2)(m+1)C例1、把下列多项式因式分解:
①25x2y3-15x2y2 ②9a(a-b)2-15(b-a)3
③8xmyn-1-12x3myn ④mn(m-n)-n(n-m)2
⑤(b-a)2-2a+2b ⑥a(x-a)(x+y)2-b(x-a)2(x+y)
例2、把下列多项式因式分解:
①6a3b2-3a2b3-18a2b3
②-4x2yz-12xy3z+4xyz
③m(1-x)-n(x-1)+p(1-x)
④-ab(a-b)2+a(b-a)2-a(a-b)2
例3、把下列多项式因式分解:
①m2-mn+mx-nx ②am+bm+an+bn+a+b
③a2b2-a2-b2+1 ④10a2x+21xy2-14ax2-15ay2
⑤2x2(-2x+9)-28x ⑥m2-mn+5n-5m(用两种方法) 1、分解因式计算 (-2)101+(-2)100
2、利用简便方法计算:
4.3x199.8+0.76x1998-1.9x199.8
3、已知 a+b=3, ab=2,
求代数式 a2 b + 2 a2 b2 +a b2 的值。
4、把 9am+1 –21 am+7a m-1分解因式
5、解方程.(x-4)2-(4-x)(8-x)=12
6、化简:1+x+x(1+x)+x(1+x)2+...+x(1+x)2015例4、分解因式的应用(1) 13.8×0.125+86.2×1/8(2)已知a+b=5,ab=3,求a2b+ab2的值. 解:原式=13.8×0.125+86.2×0.125
=0.125×(13.8+86.2)
=0.125×100
=12.5 解: a2b+ab2 =ab(a+b)=3 × 5=15因式分解应用
拓展运用:6.已知1+x+x2+x3=0.
求x+x2+x3+x4+……+x2015的值.解:原式=x(1+x+x2+x3) +x5(1+x+x2+x3) +……+ x2012(1+x+x2+x3)
= 0
6、分解因式:①4xmynb-6xm+1yn+2+2xm+2yn+1②a(x+y-z) -b(z-x-y) -c(x-z+y)③(5x-2y)2 +(2x+5y)2解:原式=2xmyn(2b-3xy2+x2y)解:原式=(x+y-z)(a+b-c)解:原式=25x2-20xy+4y2+4x2+20xy+25y2
=29x2+29y2
=29(x2+y2)3.试说明:817-279-913能被45整除.解:∵原式=(34)7- (33)9- (32)13
=328-327-326
=326(32-3-1)
=326×5
=325×45
∴817-279-913能被45整除.(1)(2)(3) 1993-199能被200整除吗?还能被哪些整数整除?谢谢 再见作业1、把下列多项式因式分解:
①6(x-2)+x(2-x) ②24a(a-b)2+18(b-a)2
③(x-y)2-(y-x)3 ④(m+1)(m-1)+(m-1)
⑤(a-3)2-2a+6 ⑥15x(a-b)2-3y(b-a)
⑦ -4a3+4a2-16a ⑧2x3+x2-6x-3 (用两种方法) 作业2、把下列多项式因式分解:
①-1/5abc+1/5ab2-a2bc ②2x(x-y)2-4x2(y-x)2
③(x-y)3-2z(y-x)2 ④(m-n)4-m(n-m)3+n(n-m)3
⑤3x(a+2b)-6xy(2b+a) ⑥7x2-3y+xy-21x(用两种方法) 作业3、把下列多项式因式分解:
①xyz2-xy2z+x2yz ②(b-a)2-2a+2b
③(2a+b)(3a-2b)-4a(2a+b) ④5(x-Y)3+10(y-x)2
⑤15x(a-b)2-3y(b-a)2 ⑥4a2+2ab+6a+3b(用两种方法) 作业4、把下列多项式因式分解:
①3ax+4ay+3bx+4by ②-2xy-4x2y+8y3y
③-3x2+12x3-3x ④-4a2-6ab-2a
⑤-8(a-b)3-4(a-b)2+2(a-b)⑥2ax-10ay+5by-bx(用两种方法)
