15.1.1 从分数到分式 课件
图片预览






文档简介
课件28张PPT。第十五章 分式问题 :
一艘轮船在静水中的最大航速是20千米/时,它沿江以最大船速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用的时间相等。江水的流速是多少?如果设江水的流速为v千米/时。15.1.1从分数到分式1.长方形的面积为10cm2,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
为______;思 考2.把体积为200cm3的水倒入底面积为 33cm2的
圆柱形容器中,水面高度为_____cm;把体积为V的
水倒入底面积为S的圆柱形容器中,
水面高度为______;思 考请大家观察式子 , , ,
与分数 , 有什么相同点和不同点。
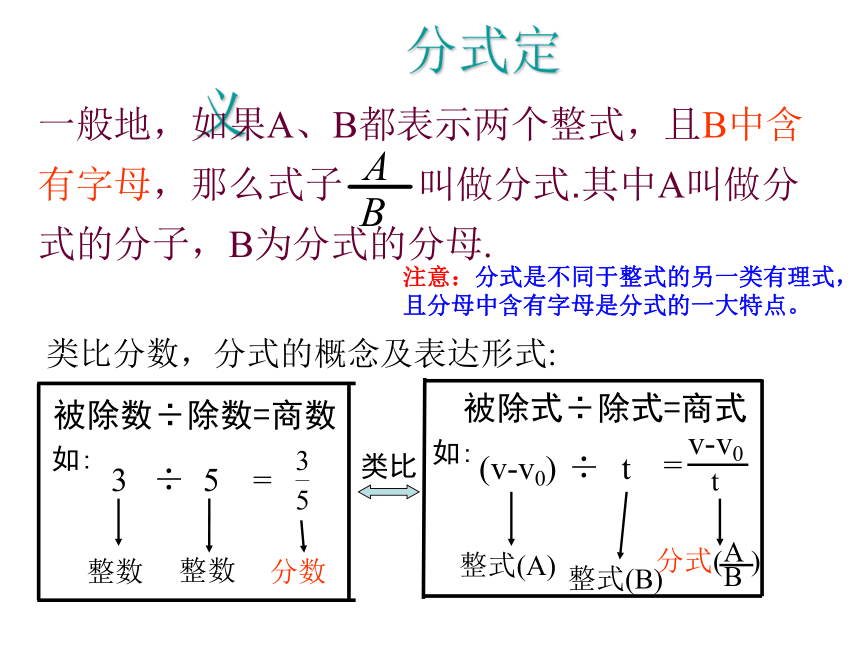
都具有分数的形式相同点不同点(观察分母)分母中有无 字母探 究 分式定义一般地,如果A、B都表示两个整式,且B中含有字母,那么式子 叫做分式.其中A叫做分式的分子,B为分式的分母.类比分数,分式的概念及表达形式:
整数整数分数
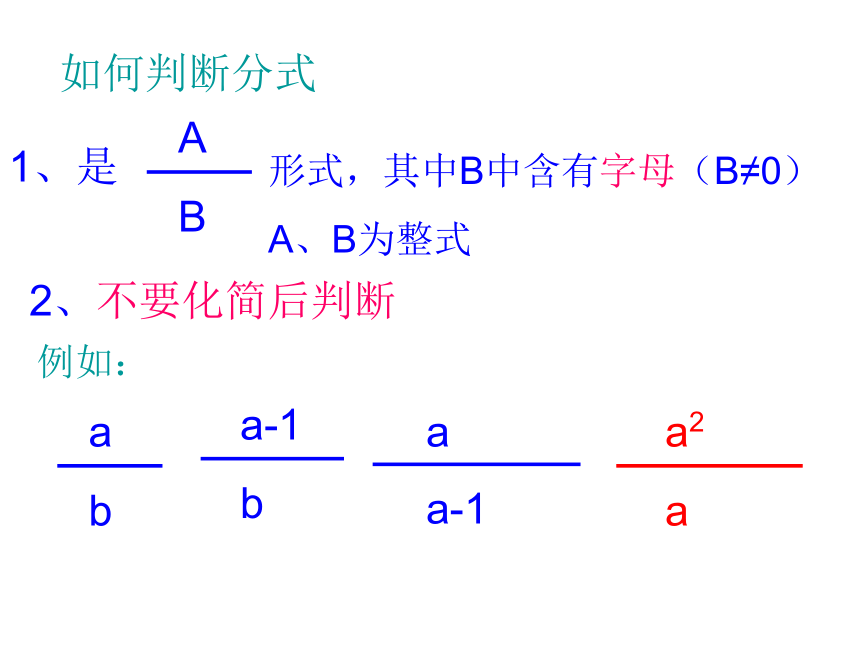
t整式(A)整式(B)类比(v-v0)÷t=v-v03 ÷ 5 = 被除数÷除数=商数如:被除式÷除式=商式如:注意:分式是不同于整式的另一类有理式,且分母中含有字母是分式的一大特点。如何判断分式2、不要化简后判断例如:判断:下面的式子哪些是分式?分式:1、分式 的分母有什么条件限制?当B=0时,分式 无意义。
当B≠0时,分式 有意义。2、当 =0时分子和分母应满足什么条件?当A=0而 B≠0时,分式值为零。探 究解:∵3X≠0
X ≠0
∴当 X ≠0时,此分式有意义解:∵X-1≠0
X ≠1
∴当 X ≠1时,此分式有意义典例分析解:∵X2-1≠0
X2 ≠1
X ≠±1
∴当 X ≠±1时,此分式有意义.___有意义时,分式(3)当X.有意义(4)当x 、 y满足关系 时,分式X+yX-y解:∵X-y≠0
X ≠y
∴当 X ≠y时,此分式有意义(2) 当x为何值时,分式有意义? (1) 当x为何值时,分式无意义?1. 已知分式 , (2)由(1)得 当x ≠-2时,分式有意义 ∴当x = -2时分式:解:(1)当分母等于零时,分式无意义。无意义。∴ x = -2即 x+2=0试一试2. 已知分式 ,(4) 当x= - 3时,分式的值是多少?(3) 当x为何值时,分式的值为零?(4)当x = -3时,解:(3)当分子等于零而分母不等于零时,分式的值为零。∴ x ≠ -2而 x+2≠0∴x = ±2则 x2 - 4=0试一试分式的符号分式的值为正:
分式的值为负:探 究分子、分母同号;(A>0,B>0或A<0,B<0)分子、分母异号;(A>0,B<0或A<0,B>0)-3 X ≥ 1
∴当 X ≥ 1时, 有意义X为何值时,下列各式有意义(求X当取值范围)2、+解: ∵1-x≥0X≥0解得:0 ≤ X≤11-x≥0
-x≥-1
X≤1∴ 0 ≤ X≤1时, 有意义+X为何值时,下列各式有意义(求X当取值范围)3、解: ∵X+1≥0X+1≠0X+1≥0
x ≥-1X+1≠0
x ≠-1解得:x >-1∴ x >-1时, 有意义由于x≠1在x≥-1的范围内,因此将x ≠1,且出去X为何值时,下列各式有意义(求X当取值范围)5、+解: ∵1+x≥0X-1≠01+x≥0
x≥-1X-1≠0
x ≠1解得:x ≥-1,且x ≠1∴ x ≥-1,且x ≠1时, 有意义+X为何值时,下列各式有意义(求X当取值范围)8、解: ∵x≥0≠0解得:x ≥0,且x ≠1≠0≠1
x ≠1由于x≠1在x≥0的范围内,因此将x ≠1,且出去∴ x ≥0,且x ≠1时, 有意义X为何值时,下列各式有意义(求X当取值范围)9、解: ∵X+1≥0≠0X+1≥0
x ≥-1≠0≠-2≠2
X+1≠4
x ≠3解得:x ≥-1,且x ≠3∴ x ≥-1,且x ≠3时, 有意义X为何值时,下列各式有意义(求X当取值范围)11、解: ∵3-2x≥03x-4>03x-4>0
3 x>4
x> ∴ 时, 有意义-2不在 范围内,所以不用且出去X为何值时,下列各式有意义(求X当取值范围)12、解: ∵5x-3≥05x-3≥0
5x ≥3解得: ,且x ≠2∴ 时, 有意义 ,且x ≠24.当x是什么数时,分式解:由x+2>0,2x-5>0得x>2.5。所以当x>2.5或x<-2时,分式的值为正。的值为正? 由x+2<0,2x-5<0得x<-2。★ 学习内容:分式的概念 数学思想:类比1.分式 有意义的条件是__________.3.分式 值为0的条件是_____________.2.分式 无意义的条件是__________.4.分式 值为正的条件是_____________.5.分式 值为负的条件是_____________.谈收获:B≠0B=0A≠0,B=0A,B同号A,B异号再 见
一艘轮船在静水中的最大航速是20千米/时,它沿江以最大船速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用的时间相等。江水的流速是多少?如果设江水的流速为v千米/时。15.1.1从分数到分式1.长方形的面积为10cm2,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
为______;思 考2.把体积为200cm3的水倒入底面积为 33cm2的
圆柱形容器中,水面高度为_____cm;把体积为V的
水倒入底面积为S的圆柱形容器中,
水面高度为______;思 考请大家观察式子 , , ,
与分数 , 有什么相同点和不同点。
都具有分数的形式相同点不同点(观察分母)分母中有无 字母探 究 分式定义一般地,如果A、B都表示两个整式,且B中含有字母,那么式子 叫做分式.其中A叫做分式的分子,B为分式的分母.类比分数,分式的概念及表达形式:
整数整数分数
t整式(A)整式(B)类比(v-v0)÷t=v-v03 ÷ 5 = 被除数÷除数=商数如:被除式÷除式=商式如:注意:分式是不同于整式的另一类有理式,且分母中含有字母是分式的一大特点。如何判断分式2、不要化简后判断例如:判断:下面的式子哪些是分式?分式:1、分式 的分母有什么条件限制?当B=0时,分式 无意义。
当B≠0时,分式 有意义。2、当 =0时分子和分母应满足什么条件?当A=0而 B≠0时,分式值为零。探 究解:∵3X≠0
X ≠0
∴当 X ≠0时,此分式有意义解:∵X-1≠0
X ≠1
∴当 X ≠1时,此分式有意义典例分析解:∵X2-1≠0
X2 ≠1
X ≠±1
∴当 X ≠±1时,此分式有意义.___有意义时,分式(3)当X.有意义(4)当x 、 y满足关系 时,分式X+yX-y解:∵X-y≠0
X ≠y
∴当 X ≠y时,此分式有意义(2) 当x为何值时,分式有意义? (1) 当x为何值时,分式无意义?1. 已知分式 , (2)由(1)得 当x ≠-2时,分式有意义 ∴当x = -2时分式:解:(1)当分母等于零时,分式无意义。无意义。∴ x = -2即 x+2=0试一试2. 已知分式 ,(4) 当x= - 3时,分式的值是多少?(3) 当x为何值时,分式的值为零?(4)当x = -3时,解:(3)当分子等于零而分母不等于零时,分式的值为零。∴ x ≠ -2而 x+2≠0∴x = ±2则 x2 - 4=0试一试分式的符号分式的值为正:
分式的值为负:探 究分子、分母同号;(A>0,B>0或A<0,B<0)分子、分母异号;(A>0,B<0或A<0,B>0)-3
∴当 X ≥ 1时, 有意义X为何值时,下列各式有意义(求X当取值范围)2、+解: ∵1-x≥0X≥0解得:0 ≤ X≤11-x≥0
-x≥-1
X≤1∴ 0 ≤ X≤1时, 有意义+X为何值时,下列各式有意义(求X当取值范围)3、解: ∵X+1≥0X+1≠0X+1≥0
x ≥-1X+1≠0
x ≠-1解得:x >-1∴ x >-1时, 有意义由于x≠1在x≥-1的范围内,因此将x ≠1,且出去X为何值时,下列各式有意义(求X当取值范围)5、+解: ∵1+x≥0X-1≠01+x≥0
x≥-1X-1≠0
x ≠1解得:x ≥-1,且x ≠1∴ x ≥-1,且x ≠1时, 有意义+X为何值时,下列各式有意义(求X当取值范围)8、解: ∵x≥0≠0解得:x ≥0,且x ≠1≠0≠1
x ≠1由于x≠1在x≥0的范围内,因此将x ≠1,且出去∴ x ≥0,且x ≠1时, 有意义X为何值时,下列各式有意义(求X当取值范围)9、解: ∵X+1≥0≠0X+1≥0
x ≥-1≠0≠-2≠2
X+1≠4
x ≠3解得:x ≥-1,且x ≠3∴ x ≥-1,且x ≠3时, 有意义X为何值时,下列各式有意义(求X当取值范围)11、解: ∵3-2x≥03x-4>03x-4>0
3 x>4
x> ∴ 时, 有意义-2不在 范围内,所以不用且出去X为何值时,下列各式有意义(求X当取值范围)12、解: ∵5x-3≥05x-3≥0
5x ≥3解得: ,且x ≠2∴ 时, 有意义 ,且x ≠24.当x是什么数时,分式解:由x+2>0,2x-5>0得x>2.5。所以当x>2.5或x<-2时,分式的值为正。的值为正? 由x+2<0,2x-5<0得x<-2。★ 学习内容:分式的概念 数学思想:类比1.分式 有意义的条件是__________.3.分式 值为0的条件是_____________.2.分式 无意义的条件是__________.4.分式 值为正的条件是_____________.5.分式 值为负的条件是_____________.谈收获:B≠0B=0A≠0,B=0A,B同号A,B异号再 见
