15.1.2 分式的基本性质 课件(2课时)
文档属性
| 名称 | 15.1.2 分式的基本性质 课件(2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-02 00:00:00 | ||
图片预览











文档简介
课件58张PPT。15.1.2 分式的基本性质
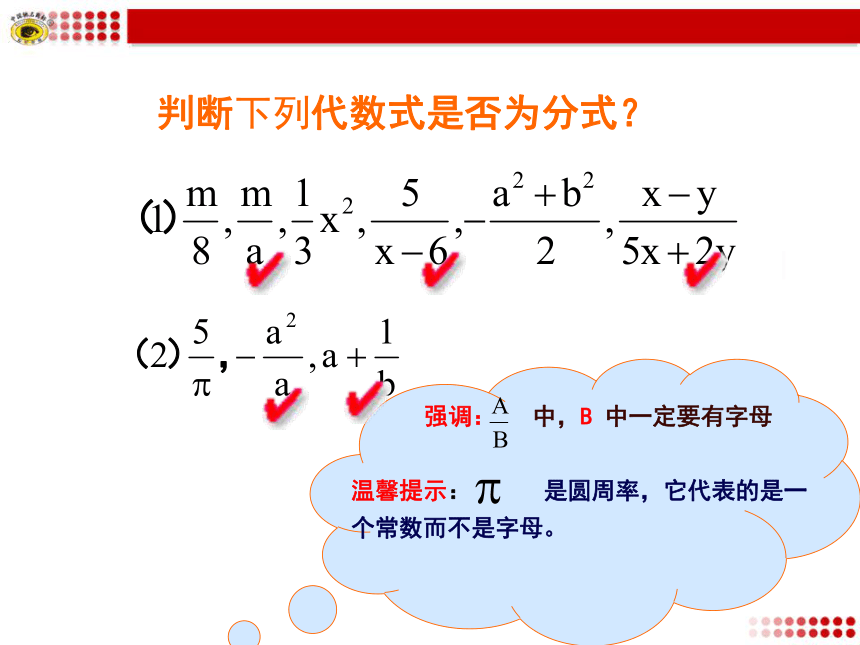
第1课时一 、复习提问B2a=1判断下列代数式是否为分式? 4.指出下列有理式中,哪些是分式?5.当x取什么数时,下列分式有意义?分母≠0√××√√×解⑴:由分子x+2=0,得 x=-2。而当 x=-2时,分母 2x-5≠0
(2)所以当x=-2时,分式 的值是零。解⑵ :由分子|x|-2=0,得 x=±2。当x=2时,分母 2x+4=4+4≠0。当x=-2时,分母 2x+4=-4+4=0。所以当x=2时,分式 的值是零。6、当 x 取什么值时,下列分式的值为零 ?(1)分数的 基本性质 分数的分子与分母同时乘以(或除以)一个不等于零的数,分数的值不变.情 境 把3个苹果平均分给6个小朋友,每个小朋友得到几个苹果?问 题 一个分数的分子、分母同乘(或除以)一个不为0的数,分数的值不变。其中a,b,c是数。 类比分数的基本性质,你能想出分式有什么性质吗? 怎样用式子表示分式的基本性质呢?思考类比分数的基本性质,得到:
分式的基本性质:
分式的分子与分母同时乘以(或除以)同一个不等于零的整式 ,分式的值不变.例1? 下列等式的右边是怎样从左边得到的?三、例题讲解与练习(2)解: (1)下列分式的右边是怎样从左边得到的? ⑴ ⑵练习 下列各组中分式,能否由第一式变形为第二式?
与
(2) 与 判 断A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍1.若把分式 中的x和y都扩大两倍,则分式的值( )【解析】选B.【跟踪训练】填空,使等式成立.
⑴ ⑵
(其中 x+y ≠0 )想一想你是怎么想的?2.填空:2x(x+y)y-2填空:分母:aba2b×a×a1×b练习1.? 填空:.三、例题讲解与练习4.下列各组分式,能否由左边变形为右边?(1) 与反思: 运用分式的基本性质应注意什么?①“都”②“同一个”③ “不为0”(2) 与(3) 与(4) 与【小结】:(1)看分母如何变化,想分子如何变化.
(2)看分子如何变化,想分母如何变化.××√√【解析】根据分式的基本性质可知,(1)分式的分子、分母同时除以9n2,此时分母为4n.
(2)分式的分子、分母同除以x,此时分母变为x.
答案:(1) 4n (2)x5. 不改变分式的值,把下列各式的分子与分母的各项系数都化为整数。解:原式 不改变分式的值,把下列各式的分子与分母的各项系数都化为整数.
⑴ ⑵ (3)例33.不改变分式的值将下列各式中的系数都化成整数.练习 不改变分式的值,使下列分子与分母都不含“-”号. 有什么发现?变号的规则是怎样的? 分式的分子、分母和分式本身的符号,同时改变其中任意两个,分式的值不变。 不改变分式的值,使下列分式的分子与分母都不含“-”号解:练习:3.下列各式中与分式 的值相等的是( ) A. B. C. D. 【解析】选B. 三、例题讲解与练习解: 不改变分式的值,使下列各式的分子与分母的最高次项系数是正数.
⑴ ⑵
⑶结练习第二课时 人要学会走路,也得学会摔跤,而且只有经过摔跤才能学会走路。
——马克思 分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变。用式子表示为:其中A,B,C是整式。复习 简单说成: 分子分母,同乘同除,始终相等。1.在下列括号内填写适当的多项式: 做这两道题的依据是: 分式的
分子的符号、
分母的符号、
分式本身的符号,
同时改变其中任意两个,分式的值不变。这两道题中分式的符号没有变化,只要考虑分子分母的符号怎样变。 分子、分母是多项式时,不要把多项式第一项的符号当成分子、分母的符号。要像提公因式一样,分子分母分别提出负号,再将两个负号消掉。
这种题在考试中以填空题形式出现,快速填空的办法是:
要想值不变,母子一起变。“—”号只是x2的“—”号才是分母的2、不改变分式的值,使下列各式的分子与分母的最高次项是正数。解:加法交换律添括号法则变符号化简下列分式:(1)解:原式=(2)解:原式= 把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分。1.约分的依据是:分式的基本性质.2.约分的基本方法是: 先把分式的分子、分母分解因式,约去公因式.3.约分的结果是:整式或最简分式(即分子
和分母没有公因式的分式)。约分: 分析:为约分要先找出分子和分母的公因式。解:化简下列分式(约分)约分的步骤
(1)约去系数的最大公约数
(2)约去分子分母相同因式的最低次幂练一练 把分式分子、分母的 公因式约去,这种变
形叫分式的约分.分式约分的依据是什么?分式的基本性质对于分数而言,彻底约分后的分数叫什么? 在化简分式 时,小颖和小明的做法出现了分歧:
小颖:
小明:
你对他们俩的解法有何看法?说说看! 彻底约分后的分式叫最简分式.一般约分要彻底, 使分子、分母没有公因式. 化简下列分式:
(1)、 (2)、【跟踪训练】约分注意:
当分子分母是多项式的时候,先进行分解因式,再约分(3)(4)通分: 分析:为通分要先确定分式的公分母,一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。解:(1)最简公分母是2a2b2c.(2)最简公分母是(x+5)(x-5).例2 通分【例题】∵ x2-y2=________________,x2+xy=_____________,∴ 与 的最简公分母为_______________,因此=________________,=________________.(x+y)(x-y)x(x+y)x(x+y)(x-y)先把分母分解因式思维拓展题1、分式的基本性质。2、分式基本性质的应用。3、分式的约分,最简分式。4、分式的通分,最简公分母。今 日 作 业课本P133习题15.1
第6题、7、9、10、11题。做一做?
例4 通分(1)(2)与与解:(1)最简公分母是(3)把各分式化成相同
分母的分式叫做
分式的通分.(2)与解:(2)最简公分母是(3)解:(2)最简公分母是 通过本课时的学习,需要我们
1.掌握分式的基本性质:分式的分子与分母乘(或除以)同一个不等于0的整式 ,分式的值不变.
2.能利用分式的基本性质对分式进行恒等变形.
3.在对分式进行变形时要注意乘(或除以) 的整式是同一个并且不等于0.
第1课时一 、复习提问B2a=1判断下列代数式是否为分式? 4.指出下列有理式中,哪些是分式?5.当x取什么数时,下列分式有意义?分母≠0√××√√×解⑴:由分子x+2=0,得 x=-2。而当 x=-2时,分母 2x-5≠0
(2)所以当x=-2时,分式 的值是零。解⑵ :由分子|x|-2=0,得 x=±2。当x=2时,分母 2x+4=4+4≠0。当x=-2时,分母 2x+4=-4+4=0。所以当x=2时,分式 的值是零。6、当 x 取什么值时,下列分式的值为零 ?(1)分数的 基本性质 分数的分子与分母同时乘以(或除以)一个不等于零的数,分数的值不变.情 境 把3个苹果平均分给6个小朋友,每个小朋友得到几个苹果?问 题 一个分数的分子、分母同乘(或除以)一个不为0的数,分数的值不变。其中a,b,c是数。 类比分数的基本性质,你能想出分式有什么性质吗? 怎样用式子表示分式的基本性质呢?思考类比分数的基本性质,得到:
分式的基本性质:
分式的分子与分母同时乘以(或除以)同一个不等于零的整式 ,分式的值不变.例1? 下列等式的右边是怎样从左边得到的?三、例题讲解与练习(2)解: (1)下列分式的右边是怎样从左边得到的? ⑴ ⑵练习 下列各组中分式,能否由第一式变形为第二式?
与
(2) 与 判 断A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍1.若把分式 中的x和y都扩大两倍,则分式的值( )【解析】选B.【跟踪训练】填空,使等式成立.
⑴ ⑵
(其中 x+y ≠0 )想一想你是怎么想的?2.填空:2x(x+y)y-2填空:分母:aba2b×a×a1×b练习1.? 填空:.三、例题讲解与练习4.下列各组分式,能否由左边变形为右边?(1) 与反思: 运用分式的基本性质应注意什么?①“都”②“同一个”③ “不为0”(2) 与(3) 与(4) 与【小结】:(1)看分母如何变化,想分子如何变化.
(2)看分子如何变化,想分母如何变化.××√√【解析】根据分式的基本性质可知,(1)分式的分子、分母同时除以9n2,此时分母为4n.
(2)分式的分子、分母同除以x,此时分母变为x.
答案:(1) 4n (2)x5. 不改变分式的值,把下列各式的分子与分母的各项系数都化为整数。解:原式 不改变分式的值,把下列各式的分子与分母的各项系数都化为整数.
⑴ ⑵ (3)例33.不改变分式的值将下列各式中的系数都化成整数.练习 不改变分式的值,使下列分子与分母都不含“-”号. 有什么发现?变号的规则是怎样的? 分式的分子、分母和分式本身的符号,同时改变其中任意两个,分式的值不变。 不改变分式的值,使下列分式的分子与分母都不含“-”号解:练习:3.下列各式中与分式 的值相等的是( ) A. B. C. D. 【解析】选B. 三、例题讲解与练习解: 不改变分式的值,使下列各式的分子与分母的最高次项系数是正数.
⑴ ⑵
⑶结练习第二课时 人要学会走路,也得学会摔跤,而且只有经过摔跤才能学会走路。
——马克思 分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变。用式子表示为:其中A,B,C是整式。复习 简单说成: 分子分母,同乘同除,始终相等。1.在下列括号内填写适当的多项式: 做这两道题的依据是: 分式的
分子的符号、
分母的符号、
分式本身的符号,
同时改变其中任意两个,分式的值不变。这两道题中分式的符号没有变化,只要考虑分子分母的符号怎样变。 分子、分母是多项式时,不要把多项式第一项的符号当成分子、分母的符号。要像提公因式一样,分子分母分别提出负号,再将两个负号消掉。
这种题在考试中以填空题形式出现,快速填空的办法是:
要想值不变,母子一起变。“—”号只是x2的“—”号才是分母的2、不改变分式的值,使下列各式的分子与分母的最高次项是正数。解:加法交换律添括号法则变符号化简下列分式:(1)解:原式=(2)解:原式= 把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分。1.约分的依据是:分式的基本性质.2.约分的基本方法是: 先把分式的分子、分母分解因式,约去公因式.3.约分的结果是:整式或最简分式(即分子
和分母没有公因式的分式)。约分: 分析:为约分要先找出分子和分母的公因式。解:化简下列分式(约分)约分的步骤
(1)约去系数的最大公约数
(2)约去分子分母相同因式的最低次幂练一练 把分式分子、分母的 公因式约去,这种变
形叫分式的约分.分式约分的依据是什么?分式的基本性质对于分数而言,彻底约分后的分数叫什么? 在化简分式 时,小颖和小明的做法出现了分歧:
小颖:
小明:
你对他们俩的解法有何看法?说说看! 彻底约分后的分式叫最简分式.一般约分要彻底, 使分子、分母没有公因式. 化简下列分式:
(1)、 (2)、【跟踪训练】约分注意:
当分子分母是多项式的时候,先进行分解因式,再约分(3)(4)通分: 分析:为通分要先确定分式的公分母,一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。解:(1)最简公分母是2a2b2c.(2)最简公分母是(x+5)(x-5).例2 通分【例题】∵ x2-y2=________________,x2+xy=_____________,∴ 与 的最简公分母为_______________,因此=________________,=________________.(x+y)(x-y)x(x+y)x(x+y)(x-y)先把分母分解因式思维拓展题1、分式的基本性质。2、分式基本性质的应用。3、分式的约分,最简分式。4、分式的通分,最简公分母。今 日 作 业课本P133习题15.1
第6题、7、9、10、11题。做一做?
例4 通分(1)(2)与与解:(1)最简公分母是(3)把各分式化成相同
分母的分式叫做
分式的通分.(2)与解:(2)最简公分母是(3)解:(2)最简公分母是 通过本课时的学习,需要我们
1.掌握分式的基本性质:分式的分子与分母乘(或除以)同一个不等于0的整式 ,分式的值不变.
2.能利用分式的基本性质对分式进行恒等变形.
3.在对分式进行变形时要注意乘(或除以) 的整式是同一个并且不等于0.
