15.2.3 整数指数幂 课件
图片预览











文档简介
课件39张PPT。15.2.3 整数指数幂整数指数幂是如何定义的?有何规定?a0 = 1 ( a ≠ 0 )复习: 新课导入 正整数指数幂的运算性质:
1.同底数的幂的乘法: (m,n是正整数);
2.幂的乘方: (m,n是正整数);
3.积的乘方: (n是正整数);
4.同底数的幂的除法: ( a≠0,m,n是正整数m>n);
5.商的乘方: (n是正整数);
6.0指数幂,即当a≠0时, . 一般地, 中指数m可以是负整数吗?如果可以,那么负整数指数幂 表示什么?【知识与能力】
1.知道负整数指数幂 (a≠0,n是正整数);
2.掌握整数指数幂的运算性质;
3.会用科学计数法表示绝对值较小的数.
【过程与方法】
通过幂指数扩展到全体整数,培养抽象的数学思维能力,运用公式进行计算,培养综合解题的能力和计算能力. ?
教学目标 【情感态度与价值观】
通过学习课堂知识懂得任何事物之间是相互联系的,理论来源于实践,服务于实践.能利用事物之间的类比性解决问题. 重点
掌握整数指数幂的运算性质,用科学记数法表示绝对值较小的数.
难点
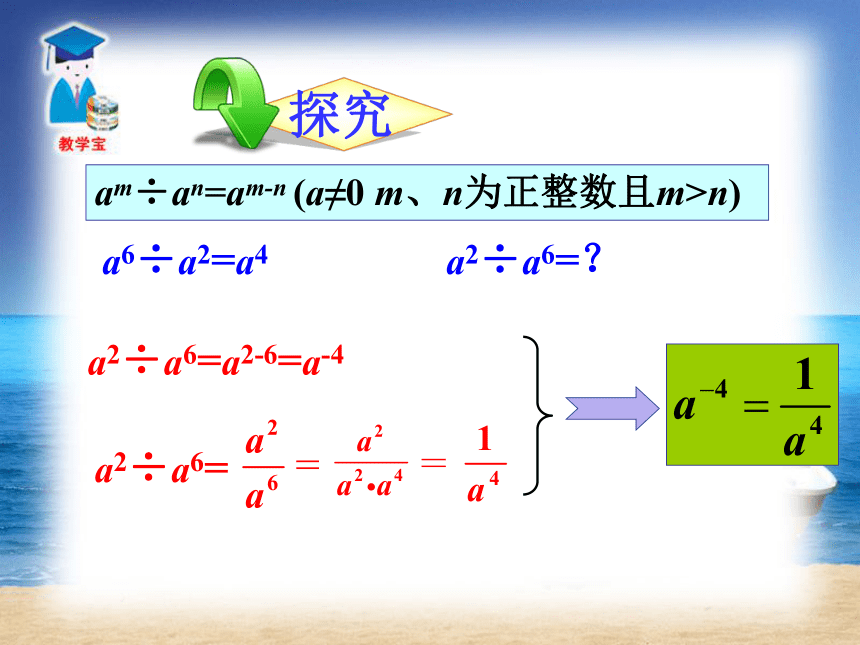
负整数指数幂公式中字母的取值范围,用科学记数法表示绝对值较小的数时,a×10n 形式中n的取值与小数中零的关系. ? 教学重难点 am÷an=am-n (a≠0 m、n为正整数且m>n)a6÷a2=a4a2÷a6=?a2÷a6=a2-6=a-4a2÷a6===这就是说:a-n(a≠0)是an的倒数.负指数的意义一般地,当n是正整数时,n是正整数时, a-n属于分式.并且(a≠0)例如: 引入负整数指数幂后,指数的取值范围就扩大到全体整数.am=am (m是正整数)1 (m=0)(m是负整数)(1)33=_____, 30=___, 3-4=_____;
(2)(-3)3=____,(-3)0=___,
(-3) -4=_____;
(3)b3=_____, b0=____, b-4=____(b≠0).91-2711小练习填空.观 察 这条性质适用于m,n是任意整数的情形仍然适用. 归纳观 察 这条性质适用于m,n是任意整数的情形仍然适用. 归纳观 察 这条性质适用于m,n是任意整数的情形仍然适用. 归纳观 察 这条性质适用于m,n是任意整数的情形仍然适用. 归纳 类似于上面的观察,进一步用负整数指数幂或0指数幂,验证 在整数指数范围内是适用.【例1】计算:解:【例2】下列等式是否正确?为什么?解:下列等式是否成立?并说明理由.光速:300 000 000=3×108米/秒;
太阳半径:696 000=6.96×105千米;
目前我国人口:6 100 000 000=6.1×109. 在七年级我们学过,一些较大的数字可以用科学记数法来表示:0.0000432= = 小于1的数也可以用科学计数法表示.0.000001= =a 是整数位只有一位的正数,n是正整数.0.0000056= = 对于一个小于1的正小数,如果小数点后至第一个非0数字前有9个0,用科学计数法表示这个数时,10的指数是多少?如果有m个0呢?0.000 000 000 52=___________,0.000 000 48=___________,0.000 000……001=__________,m个05.2×10-104.8×10-7 【例3】纳米(符号为nm)是长度单位,原称毫微米,就是10-9米(10亿分之一米),即10-6毫米(100万分之一毫米).如同厘米、分米和米一样,是长度的度量单位.相当于4倍原子大小,比单个细菌的长度还要小.单个细菌用肉眼是根本看不到的,用显微镜测直径大约是五微米.
请你算一算:5立方毫米的空间可以放多少个1立方纳米的物体?解:用科学计数法表示下列各数:
0.00001,-0.025,0.00000032,
0.000406 小练习2.计算:
(1)(5×10-4) ×(1.8×105);
(2) (4×10-7)3÷(10-5)2.3.用科学计数法把0.000 005 042表示成
5.042×10n,那么n=___.690小练习1.n是正整数时, a-n属于分式.并且(a≠0)2.科学计数法表示小于1的小数:(a是整数位只有一位的正数,n是正整数.) 课堂小结 1.用科学计数法表示下列数:
0.000 000 004, 0.0035,
-0.000 000 254 , -0.000 04,
0.000 000 040 35, 5 870 000. 随堂练习 2.一种细菌的半径是0.000 04米,用科学记数法可以把它表示为_________米. 3.探索规律:31=3,个位数字是3;32=9,个位数字式9;33=27,个位数字是7;34=81,个位数字是1;35=243,个位数字是3;36=729,个位数字是9;……那么,37的个位数字是______,320的个位数字是______.734.计算.5.已知:10m=5,10n=4,求102m-3n.解:6. 已知,求的值. ∴原式= =解:∵=即:习题答案 3.(1)x≠0 ; (2)x≠3 ;
(3)x≠ ; (4)x≠±4。4.(1)是,约分;(2)是,约分;
(3)是,约分;(4)是,约分。
1.同底数的幂的乘法: (m,n是正整数);
2.幂的乘方: (m,n是正整数);
3.积的乘方: (n是正整数);
4.同底数的幂的除法: ( a≠0,m,n是正整数m>n);
5.商的乘方: (n是正整数);
6.0指数幂,即当a≠0时, . 一般地, 中指数m可以是负整数吗?如果可以,那么负整数指数幂 表示什么?【知识与能力】
1.知道负整数指数幂 (a≠0,n是正整数);
2.掌握整数指数幂的运算性质;
3.会用科学计数法表示绝对值较小的数.
【过程与方法】
通过幂指数扩展到全体整数,培养抽象的数学思维能力,运用公式进行计算,培养综合解题的能力和计算能力. ?
教学目标 【情感态度与价值观】
通过学习课堂知识懂得任何事物之间是相互联系的,理论来源于实践,服务于实践.能利用事物之间的类比性解决问题. 重点
掌握整数指数幂的运算性质,用科学记数法表示绝对值较小的数.
难点
负整数指数幂公式中字母的取值范围,用科学记数法表示绝对值较小的数时,a×10n 形式中n的取值与小数中零的关系. ? 教学重难点 am÷an=am-n (a≠0 m、n为正整数且m>n)a6÷a2=a4a2÷a6=?a2÷a6=a2-6=a-4a2÷a6===这就是说:a-n(a≠0)是an的倒数.负指数的意义一般地,当n是正整数时,n是正整数时, a-n属于分式.并且(a≠0)例如: 引入负整数指数幂后,指数的取值范围就扩大到全体整数.am=am (m是正整数)1 (m=0)(m是负整数)(1)33=_____, 30=___, 3-4=_____;
(2)(-3)3=____,(-3)0=___,
(-3) -4=_____;
(3)b3=_____, b0=____, b-4=____(b≠0).91-2711小练习填空.观 察 这条性质适用于m,n是任意整数的情形仍然适用. 归纳观 察 这条性质适用于m,n是任意整数的情形仍然适用. 归纳观 察 这条性质适用于m,n是任意整数的情形仍然适用. 归纳观 察 这条性质适用于m,n是任意整数的情形仍然适用. 归纳 类似于上面的观察,进一步用负整数指数幂或0指数幂,验证 在整数指数范围内是适用.【例1】计算:解:【例2】下列等式是否正确?为什么?解:下列等式是否成立?并说明理由.光速:300 000 000=3×108米/秒;
太阳半径:696 000=6.96×105千米;
目前我国人口:6 100 000 000=6.1×109. 在七年级我们学过,一些较大的数字可以用科学记数法来表示:0.0000432= = 小于1的数也可以用科学计数法表示.0.000001= =a 是整数位只有一位的正数,n是正整数.0.0000056= = 对于一个小于1的正小数,如果小数点后至第一个非0数字前有9个0,用科学计数法表示这个数时,10的指数是多少?如果有m个0呢?0.000 000 000 52=___________,0.000 000 48=___________,0.000 000……001=__________,m个05.2×10-104.8×10-7 【例3】纳米(符号为nm)是长度单位,原称毫微米,就是10-9米(10亿分之一米),即10-6毫米(100万分之一毫米).如同厘米、分米和米一样,是长度的度量单位.相当于4倍原子大小,比单个细菌的长度还要小.单个细菌用肉眼是根本看不到的,用显微镜测直径大约是五微米.
请你算一算:5立方毫米的空间可以放多少个1立方纳米的物体?解:用科学计数法表示下列各数:
0.00001,-0.025,0.00000032,
0.000406 小练习2.计算:
(1)(5×10-4) ×(1.8×105);
(2) (4×10-7)3÷(10-5)2.3.用科学计数法把0.000 005 042表示成
5.042×10n,那么n=___.690小练习1.n是正整数时, a-n属于分式.并且(a≠0)2.科学计数法表示小于1的小数:(a是整数位只有一位的正数,n是正整数.) 课堂小结 1.用科学计数法表示下列数:
0.000 000 004, 0.0035,
-0.000 000 254 , -0.000 04,
0.000 000 040 35, 5 870 000. 随堂练习 2.一种细菌的半径是0.000 04米,用科学记数法可以把它表示为_________米. 3.探索规律:31=3,个位数字是3;32=9,个位数字式9;33=27,个位数字是7;34=81,个位数字是1;35=243,个位数字是3;36=729,个位数字是9;……那么,37的个位数字是______,320的个位数字是______.734.计算.5.已知:10m=5,10n=4,求102m-3n.解:6. 已知,求的值. ∴原式= =解:∵=即:习题答案 3.(1)x≠0 ; (2)x≠3 ;
(3)x≠ ; (4)x≠±4。4.(1)是,约分;(2)是,约分;
(3)是,约分;(4)是,约分。
