沪教版数学高一下册4.4_对数的概念及其运算课件(29张ppt
文档属性
| 名称 | 沪教版数学高一下册4.4_对数的概念及其运算课件(29张ppt |

|
|
| 格式 | zip | ||
| 文件大小 | 771.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-04 13:22:11 | ||
图片预览








文档简介
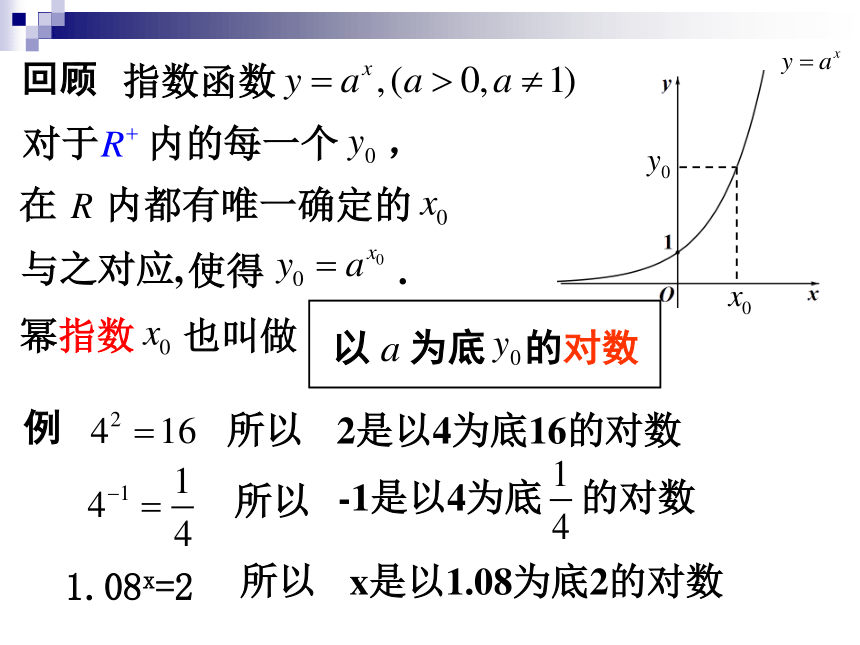
课件29张PPT。第四章 幂函数、指数函数和对数函数4.4. 对数的概念及运算一、引例我国现在国民生产总值为a亿元,如果我国国民生产总值的平均增长率为8%,那么经过多少年后生产总值是现在的2倍?解:设经过x年我国生产总值是现在的2倍由题意得:a(1+0.08)x=2a即1.08x=2x=?回顾指数函数对于 内的每一个 ,在 内都有唯一确定的与之对应,幂指数 也叫做以 为底 的对数例所以2是以4为底16的对数所以-1是以4为底 的对数使得 .1.08x=2所以x是以1.08为底2的对数二、对数(Logarithms)的概念一般地,如果 的 次幂等于 ,即那么 就叫做以 为底 的对数,其中 叫做对数的底数;叫做真数读作 “ 等于以 为底 的对数”例记作 ,即既是符号
又是算式对数恒等式:____________由对数定义可知:①②零与负数没有对数,即_______1的对数为零,即__________底数的对数为1,即__________③④二、对数概念(常用对数与自然对数)通常将以10为底的对数称为常用对数对数 简记为例把以常数 为底的对数称为自然对数其中 是一个无理数(超越数) 对数 简记为例例1.把下列对数式与指数式互换:(1)(2)(3)(4)(5)(6)(7)(8)三、对数式的转化注:指数式与对数式的互换常用于计算、式子变形,须注意a、b、N的位置例2.利用计算器计算下列对数的值(保留至0.001)(卡西欧 fx-82ES为例)(1)(2)四、对数式的性质例3.利用计算器计算下列对数的值(保留至0.01)观察:分类比较论证:利用指数式猜想:计算观察猜想论证请用此方法推广出其他底数的对数性质课堂自测:1. 指数式与对数式互换,并找出错误的等式.(1)(2)(3)(4)(5)(6)2.利用对数解下列方程:(1)(2)3.求下列各式的值:(3)(1)(2)(3)(4)4.已知求证:课堂自测答案:1.(2)(3)(4)(5)错误(6)2.(1)(2)(3)4.证:设(1)3.(1)(2)(3)(4)是单调函数即证毕小结对数 满足:对数的正负性与底数及真数的大小的关系对数恒等式:____________①②零与负数没有对数,即_______1的对数为零,即__________底数的对数为1,即__________③④五、对数的运算性质计算填表:P8观察:猜想:如果论证:利用指数式证明:解:记则同理真数集合A对数集合B五、(一)积、商、幂的对数已知,那么(1)(2)(3)可以推广为若干个正因数的积:请用文字语言叙述上述三个等式例1.用 表示下列各式:(1)(2)(3)(4)思考例2. 利用积、商、幂的对数求值:(1)(2)(3)(4)化成底数的幂形式实际应用P9课堂自测:(1)(2)(3)(4)2.计算:(1)(2)3.已知 ,不用计算器求值:(3)(1)(2)1.用 表示下列各式:(4)4.(1) 求证:(2)已知 求证:课堂自测答案:1.(1)(2)(3)(4)2.(1) 1 (2) 1 (3) 6 (4) 13.(1)(2)4.(1)证:证毕(2)证:证毕探究 试用常用对数表示解:设则两边取常用对数,得所以因此一、换底公式一般地有下面的的对数换底公式其中换成常用对数的换底公式为:例例1.利用换底公式计算:(1)(2)(3)例2. 利用换底公式证明:(1)(2)证明: (1)(2)证毕(选用)例3.已知 ,求解:解毕课堂自测:1.计算:2.化为 的形式:3.“从左至右”进行证明:(1)(3)(4)(2)(1)(2)(3)(1)(2)(3)课堂自测答案:1.(1)(2)(3)2.(1)(2)(3)3.证明:(1)(2)(3)(4)
又是算式对数恒等式:____________由对数定义可知:①②零与负数没有对数,即_______1的对数为零,即__________底数的对数为1,即__________③④二、对数概念(常用对数与自然对数)通常将以10为底的对数称为常用对数对数 简记为例把以常数 为底的对数称为自然对数其中 是一个无理数(超越数) 对数 简记为例例1.把下列对数式与指数式互换:(1)(2)(3)(4)(5)(6)(7)(8)三、对数式的转化注:指数式与对数式的互换常用于计算、式子变形,须注意a、b、N的位置例2.利用计算器计算下列对数的值(保留至0.001)(卡西欧 fx-82ES为例)(1)(2)四、对数式的性质例3.利用计算器计算下列对数的值(保留至0.01)观察:分类比较论证:利用指数式猜想:计算观察猜想论证请用此方法推广出其他底数的对数性质课堂自测:1. 指数式与对数式互换,并找出错误的等式.(1)(2)(3)(4)(5)(6)2.利用对数解下列方程:(1)(2)3.求下列各式的值:(3)(1)(2)(3)(4)4.已知求证:课堂自测答案:1.(2)(3)(4)(5)错误(6)2.(1)(2)(3)4.证:设(1)3.(1)(2)(3)(4)是单调函数即证毕小结对数 满足:对数的正负性与底数及真数的大小的关系对数恒等式:____________①②零与负数没有对数,即_______1的对数为零,即__________底数的对数为1,即__________③④五、对数的运算性质计算填表:P8观察:猜想:如果论证:利用指数式证明:解:记则同理真数集合A对数集合B五、(一)积、商、幂的对数已知,那么(1)(2)(3)可以推广为若干个正因数的积:请用文字语言叙述上述三个等式例1.用 表示下列各式:(1)(2)(3)(4)思考例2. 利用积、商、幂的对数求值:(1)(2)(3)(4)化成底数的幂形式实际应用P9课堂自测:(1)(2)(3)(4)2.计算:(1)(2)3.已知 ,不用计算器求值:(3)(1)(2)1.用 表示下列各式:(4)4.(1) 求证:(2)已知 求证:课堂自测答案:1.(1)(2)(3)(4)2.(1) 1 (2) 1 (3) 6 (4) 13.(1)(2)4.(1)证:证毕(2)证:证毕探究 试用常用对数表示解:设则两边取常用对数,得所以因此一、换底公式一般地有下面的的对数换底公式其中换成常用对数的换底公式为:例例1.利用换底公式计算:(1)(2)(3)例2. 利用换底公式证明:(1)(2)证明: (1)(2)证毕(选用)例3.已知 ,求解:解毕课堂自测:1.计算:2.化为 的形式:3.“从左至右”进行证明:(1)(3)(4)(2)(1)(2)(3)(1)(2)(3)课堂自测答案:1.(1)(2)(3)2.(1)(2)(3)3.证明:(1)(2)(3)(4)
