沪教版数学高一下册4.5反函数的概念课件(34张ppt
文档属性
| 名称 | 沪教版数学高一下册4.5反函数的概念课件(34张ppt |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-04 00:00:00 | ||
图片预览










文档简介
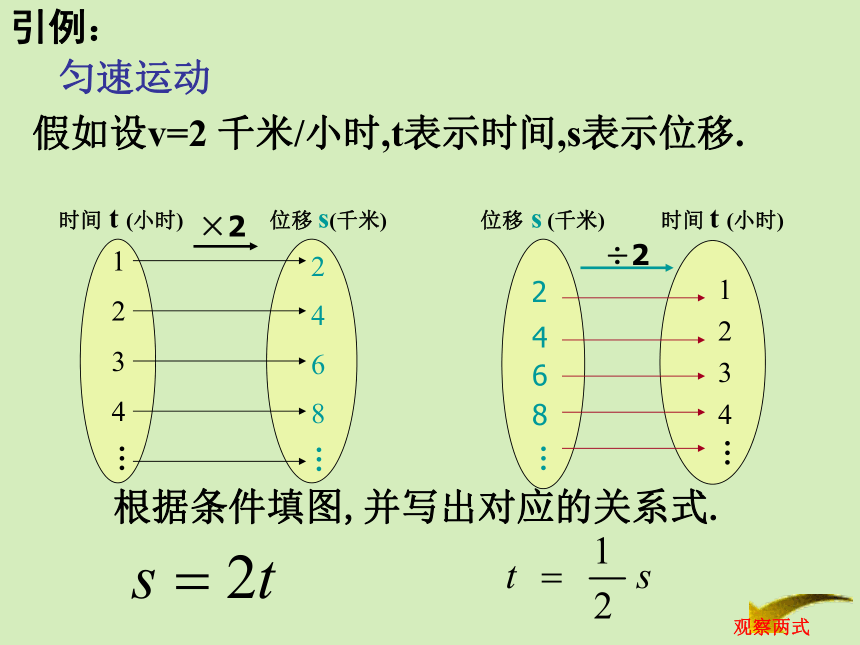
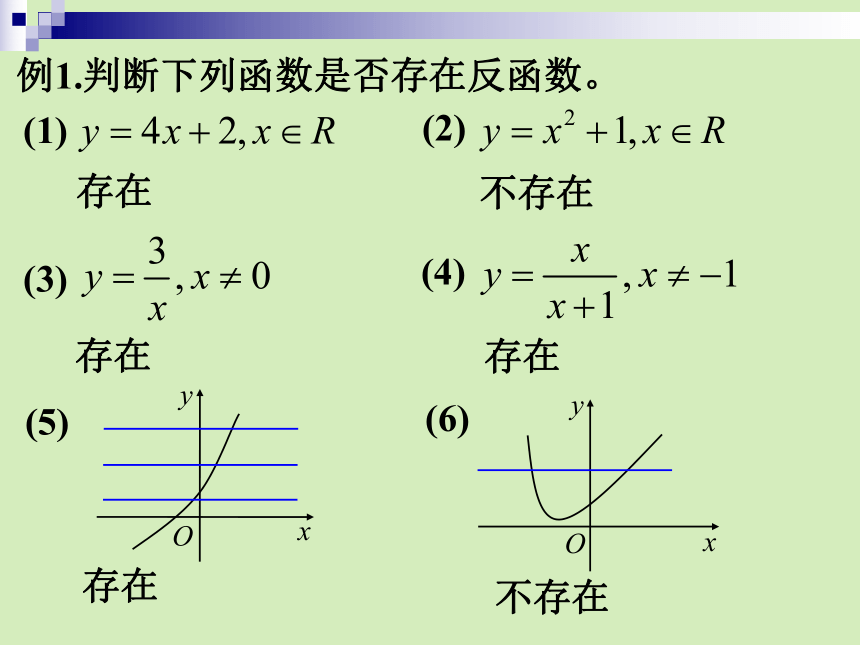
课件34张PPT。第四章 幂函数、指数函数和对数函数4.5 反函数的概念假如设v=2 千米/小时,t表示时间,s表示位移.根据条件填图,并写出对应的关系式.匀速运动引例:在①中t是自变量,s是自变量t的函数.在②中s是自变量,t是自变量s的函数.除此之外,我们还可发现②的表达式可由①的表达式变换而得,即从①式中求出t即可.得到反函数的概念一、反函数的概念一般地,对于函数若对于 中任意一个值 ,都有 中唯一的使得,那么在 上就确定了的反函数,记作例的反函数就是正偶数集函数与函数互为反函数!思考:函数 的因变量 与自变量的对应关系逆过来,能否构成函数?函数 的因变量 与自变量的对应关系逆过来,能否构成函数?反函数的存在性例1.判断下列函数是否存在反函数。(1)(2)(3)(4)(5)(6)存在不存在存在存在存在不存在二、一个函数存在反函数的判定记(1)对于任意 ,若 ,则(或 若 ,则 )(2)函数 是单调函数.(充分非必要条件)(3)函数 的图像符合“水平线检验法”(4)由 解得的 也是一个函数.上述所有方法都可说明函数存在反函数,即 是“一对一”的.三、求一个函数的反函数例 求函数 的反函数.解: 的值域为求 得所以反函数为为了在同一坐标系内作出一个函数表示,因变量用 表示.因此,反函数改写为与其反函数的图像,习惯上自变量用例2.求下列函数的反函数.(1)(2)(3)(4)解: (1)因此反函数为(2)解得:解得:因此反函数为例2.求下列函数的反函数.(3)(4)解: (3)因此反函数为(4)解得:解得:因此反函数为解毕反函数的概念小结存在反函数的是一一对应的与函数 与函数互为反函数.充要条件是:求 的反函数的一般步骤为:①求值域(即反函数的定义域)②求方程 的解③改写为反函数(1)(2)(3)则对应法互逆,定义域、值域互反.∵ ?1≤ x < 0∴解:∴ 0 ≤< 1∴0 < y ≤ 1解得(∵ ?1≤ x < 0 )由(?1≤ x < 0)的反函数是:( 0 < x ≤1 )∴0 < x2 ≤ 1∴0≤1 ? x2 < 1.反函数的练习:(2)函数y=2|x|在下列哪个定义区间内不存在反函数? ( )
(A)[2,4]; (B)[-4,4]
(C)[0,+∞) (D(-∞,0]B有时原函数和反函数是同一个函数单调函数必有反函数(3)已知 ,求解:因此解法二:设因此即点 在 图像上即点 在 图像上解得解毕(第2课时)课前练习:例1. 求函数y=3x-2的反函数,
并画出原函数和反函数的图像.解 ∵y=3x-2 x∈R(一)例题讲解反函数的图像.例2.求函数 的反函数,并在同一坐标系中画出它们的图像.解:的值域为的反函数是一、互为反函数的函数图像间的关系定理 函数 和它的反函数 的图像关于直线 对称.证:设 是 的图像上
任意一点.因此是 的反函数因此即 在反函数 图像上.一、互为反函数的函数图像间的关系定理 函数 和它的反函数 的图像关于直线 对称.续证:对称.图像上任意一点关于是 上任意一点,直线 的对称点都在 的图像上.由于 与 互为反函数,故以上结论反之也成立. 与 关于直线证毕例2.求函数 的反函数,并在同一坐标系中画出它们的图像.解:的值域为的反函数是思考 函数的图像与其反函数的图像
有什么有怎样的位置关系?平移有何规律?例.求函数y=x3(x∈R)的反函数,并画出原来的函数和它的反函数的图象.解:原函数与y=x的交点个数?
反函数与y=x的交点个数?
原函数与反函数的交点个数及位置?
例4.求证:函数 的图像关于直线对称.分析:由于存在反函数,且因此,即证证:因此 的图像关于直线 对称.与 的图像关于 对称,证毕若函数y=f(x)的图像关于直线y=x对称,那么它存在反函数,且反函数是它本身。练习二、单调函数的反函数的单调性(选用)例4.若函数 是 上的单调函数,探究 单调性.证明:不妨设 是增函数存在唯一的使得:即是增函数是增函数定理 单调函数的反函数也是单调函数且两个函数具有相同的单调性.二、单调函数的反函数的单调性但单调区间不一定相同反函数中的奇偶性问题一般地,偶函数不存在反函数。除了y=c,x?{0},c为常数。奇函数不一定存在反函数,
若存在,反函数也是奇函数。如何证明? 复合函数中反函数问题反函数结论总结原、反函数的对应法互逆,定义域、值域互反.求反函数3步骤:定义域,反解,改写原、反函数图像关于直线y=x 对称.(a,b)在原函数图像上,(b,a)在反函数图像上反函数结论总结(续)原、反函数交点或在直线y=x上,或成对出现且关于直线y=x 对称单调函数的反函数也是单调函数,且单调性一致,但单调区间不一定相同一般地,偶函数不存在反函数。
除了y=c,x?{0},c为常数。奇函数不一定有反函数,若有则也是奇函数。反函数结论总结(续)原函数左移a个单位、则反函数下移a个单位
(A)[2,4]; (B)[-4,4]
(C)[0,+∞) (D(-∞,0]B有时原函数和反函数是同一个函数单调函数必有反函数(3)已知 ,求解:因此解法二:设因此即点 在 图像上即点 在 图像上解得解毕(第2课时)课前练习:例1. 求函数y=3x-2的反函数,
并画出原函数和反函数的图像.解 ∵y=3x-2 x∈R(一)例题讲解反函数的图像.例2.求函数 的反函数,并在同一坐标系中画出它们的图像.解:的值域为的反函数是一、互为反函数的函数图像间的关系定理 函数 和它的反函数 的图像关于直线 对称.证:设 是 的图像上
任意一点.因此是 的反函数因此即 在反函数 图像上.一、互为反函数的函数图像间的关系定理 函数 和它的反函数 的图像关于直线 对称.续证:对称.图像上任意一点关于是 上任意一点,直线 的对称点都在 的图像上.由于 与 互为反函数,故以上结论反之也成立. 与 关于直线证毕例2.求函数 的反函数,并在同一坐标系中画出它们的图像.解:的值域为的反函数是思考 函数的图像与其反函数的图像
有什么有怎样的位置关系?平移有何规律?例.求函数y=x3(x∈R)的反函数,并画出原来的函数和它的反函数的图象.解:原函数与y=x的交点个数?
反函数与y=x的交点个数?
原函数与反函数的交点个数及位置?
例4.求证:函数 的图像关于直线对称.分析:由于存在反函数,且因此,即证证:因此 的图像关于直线 对称.与 的图像关于 对称,证毕若函数y=f(x)的图像关于直线y=x对称,那么它存在反函数,且反函数是它本身。练习二、单调函数的反函数的单调性(选用)例4.若函数 是 上的单调函数,探究 单调性.证明:不妨设 是增函数存在唯一的使得:即是增函数是增函数定理 单调函数的反函数也是单调函数且两个函数具有相同的单调性.二、单调函数的反函数的单调性但单调区间不一定相同反函数中的奇偶性问题一般地,偶函数不存在反函数。除了y=c,x?{0},c为常数。奇函数不一定存在反函数,
若存在,反函数也是奇函数。如何证明? 复合函数中反函数问题反函数结论总结原、反函数的对应法互逆,定义域、值域互反.求反函数3步骤:定义域,反解,改写原、反函数图像关于直线y=x 对称.(a,b)在原函数图像上,(b,a)在反函数图像上反函数结论总结(续)原、反函数交点或在直线y=x上,或成对出现且关于直线y=x 对称单调函数的反函数也是单调函数,且单调性一致,但单调区间不一定相同一般地,偶函数不存在反函数。
除了y=c,x?{0},c为常数。奇函数不一定有反函数,若有则也是奇函数。反函数结论总结(续)原函数左移a个单位、则反函数下移a个单位
