4.3.2 角的比较与运算课件
图片预览






文档简介
课件35张PPT。4.3.2 角的比较与运算第四章 图形初步认识导入新课讲授新课当堂练习课堂小结4.3 角【义务教育教科书人教版七年级上册】1. 掌握角的大小的比较方法. (重点)
2. 理解角平分线和角的和、差、倍、分的意义及数量
关系,能够用几何语言进行相关表述,并能解答相
关问题. (重点、难点)
3. 会进行涉及度、分、秒的角度的计算. (重点、难点)
有一天学生张亮和王帅各带了一把折扇(如图所示),下面是他们的一段对话:
张:我的折扇张开大一些,所以我的折扇的角也大一些.
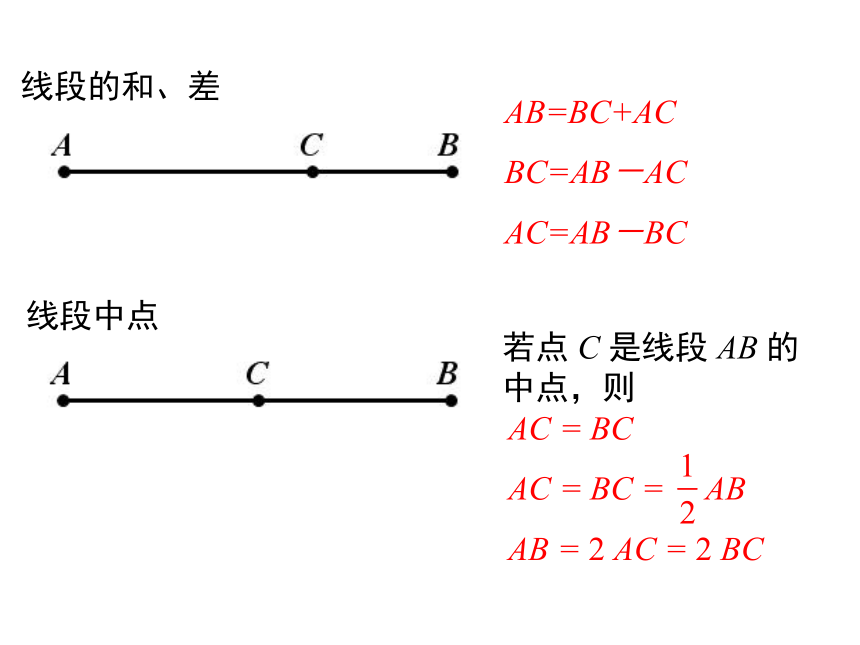
王:我的折扇长一些,所以我的折扇的角也大一些.导入新课情境引入同学们,你们有办法帮他们进行判断吗?ABCDEF怎样比较∠ABC和∠DEF的大小?线段长短的比较AB>CDABBC=AB-AC
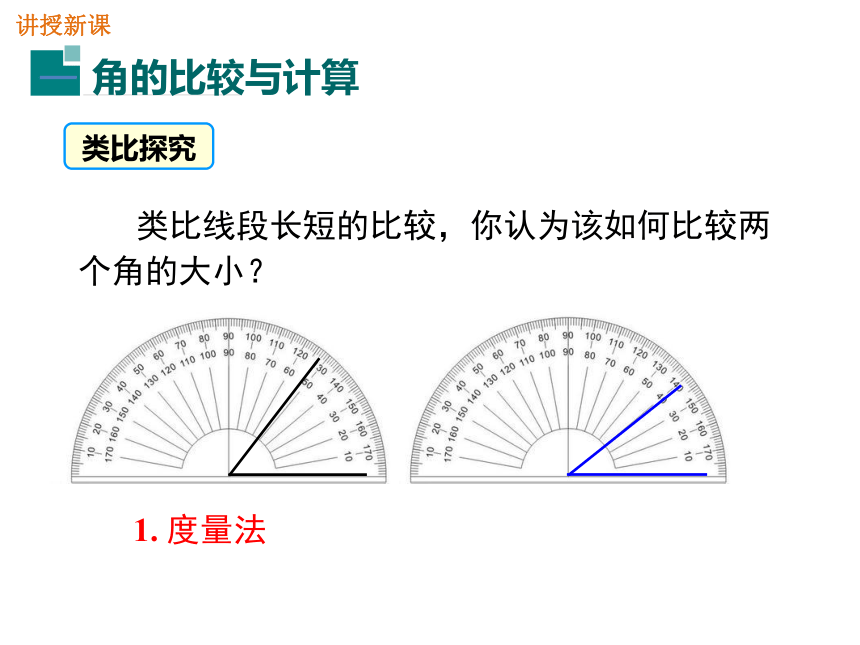
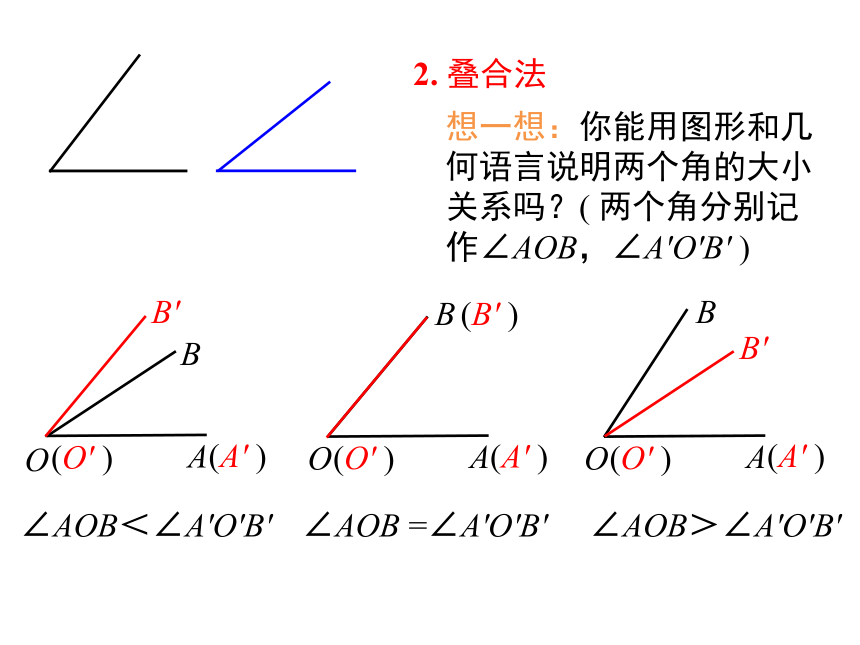
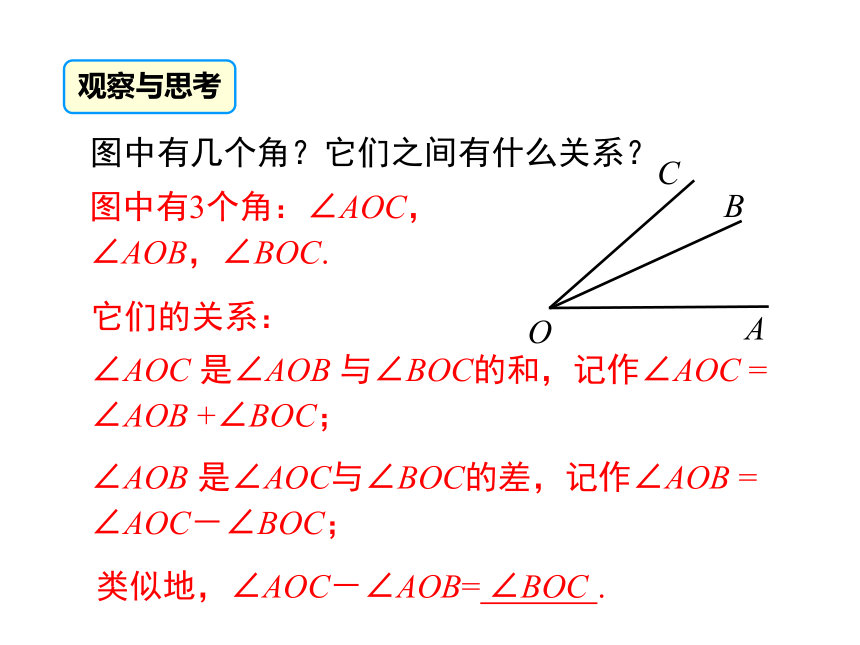
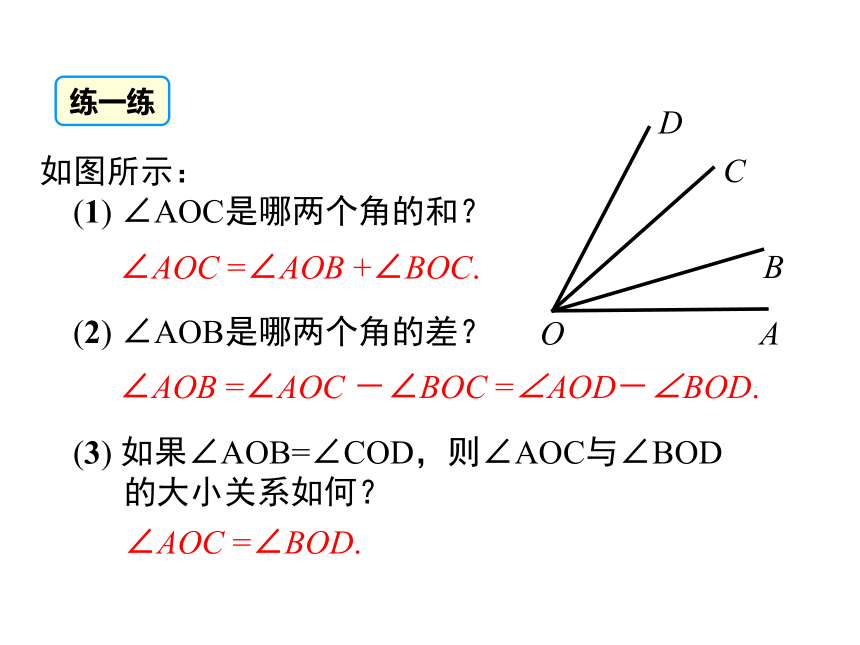
AC=AB-BC线段的和、差线段中点若点 C 是线段 AB 的中点,则讲授新课 类比线段长短的比较,你认为该如何比较两个角的大小?1. 度量法类比探究2. 叠合法想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )∠AOB<∠A'O'B'∠AOB =∠A'O'B'∠AOB>∠A'O'B'图中有几个角?它们之间有什么关系?图中有3个角:∠AOC,∠AOB,∠BOC.∠AOC 是∠AOB 与∠BOC的和,记作∠AOC = ∠AOB +∠BOC;它们的关系:∠AOB 是∠AOC与∠BOC的差,记作∠AOB = ∠AOC-∠BOC;类似地,∠AOC-∠AOB= .观察与思考∠BOC练一练如图所示:
(1) ∠AOC是哪两个角的和?
(2) ∠AOB是哪两个角的差?
(3) 如果∠AOB=∠COD,则∠AOC与∠BOD
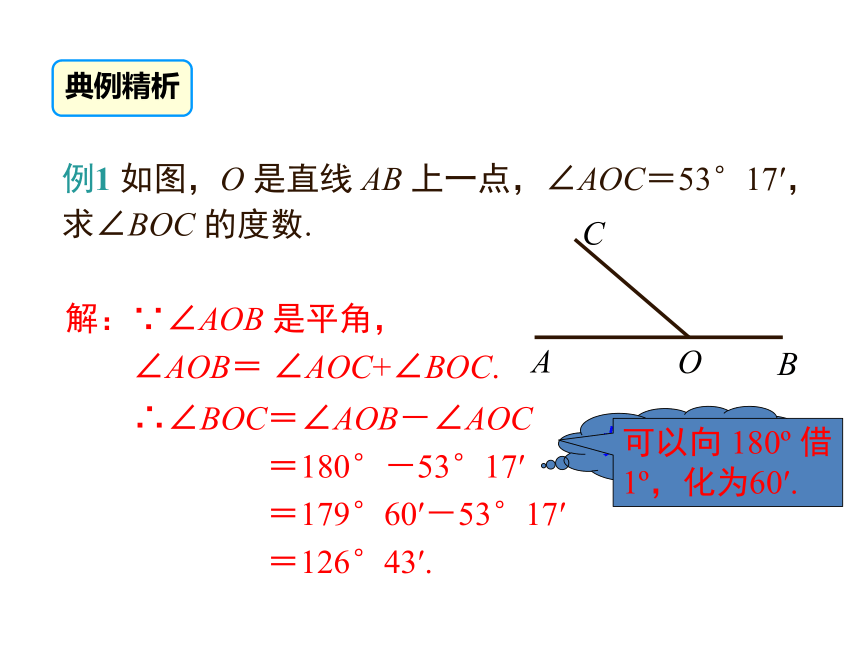
的大小关系如何?∠AOC =∠AOB +∠BOC.∠AOB =∠AOC -∠BOC =∠AOD-∠BOD.∠AOC =∠BOD.例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,
求∠BOC 的度数.解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.典例精析(2) 如图②,若∠AOB= 60°,∠BOC=40°,则
∠AOC= °.
(1) 如图①,若∠AOC=35°,∠BOC=40°,则
∠AOB= °. 7520图① 图②变式训练(3) 若∠AOB =60°,∠AOC =30°,则∠BOC
= °. 90或30提示:无图条件下要分情况讨论. 如图,借助一副三角尺可以画出15°和75°的角,你还能画出哪些度数的角?试一试:75°15°例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.(1) 120°-38°41′; (2)67°31′+48°49′. 解:原式 = 119°60′-38°41′
= 81°19′ .解:原式 = (67+48)°+(31+49)′
= 115°97′
= 116°37′ .变式训练计算方法总结:涉及到度、分、秒的角度的加与减,要将度与度、分与分、秒与秒分别相加、减,分秒相加时逢60要进位,相减时要借1作60.练一练1. 20°30′×8; 2. 106°6′÷5. 解:原式 = (106÷5)°+(6÷5)′= 21°+1°÷5
+(6÷5)′= 21°+(66÷5)′=21°+13′+1′÷5
=21°+13′+60″÷5=21°13′12″解:原式 = 20°×8+30′×8
= 160°240′
= 164°互动探究 动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:∠AOC_____∠COB;∠AOB=_____∠AOC.=2 一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线. 应用格式:OBAC∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?解:因为 OB 平分∠AOC,
∠AOC=80°,(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD
是多少度?
解:因为 OB 平分∠AOC,所以 ∠BOC=∠AOB = 40°.因为 OD 平分∠COE,所以∠COD=∠DOE = 30°,所以
∠BOD =∠BOC+∠COD = 40°+30°= 70°.(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB
是多少度?解:因为 ∠COD=30°,
OD 平分∠COE,所以 ∠COE=2∠COD=60°,所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.又因为 OB 平分∠AOC,例4 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3.求OC与∠AOB的平分线所成的角的度数.解:分以下两种情况: 设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,∴2x+3x=40°,得x=8°,
∴∠AOC=2x=2×8°=16°.
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOD-∠AOC=20°-16°=4°. ?如图,OC在∠AOB内部,OD平分∠AOB,∴设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,
∴3x-2x=40°,得x=40°,
∴∠AOC=2x=2×40°=80°,
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOC+∠AOD=80°+20°=100°.
?如图,OC在∠AOB外部,OD平分∠AOB,∴OC与∠AOB的平分线所成的角的度数为4°或100°.方法总结:涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想和分类讨论思想解决问题.1. 如图:OC是∠AOB的平分线,OD是∠BOC的平
分线,那么下列各式中正确的是 ( )
A做一做2. 如图,OC是平角∠AOB的角平分线,∠COD=32°,
求∠AOD的度数.答案:∠AOD=122°.当堂练习1. 如图,∠AOB=∠COD=90,∠AOD=146°,则
∠BOC=____.2. 已知∠AOB=38°,∠BOC=25°,那么∠AOC
的度数是 .
34°13°或63°3. 如图,∠AOB=170°,∠AOC =∠BOD=90°,求∠COD的度数
答案:∠COD=10°.(1) 12°36′56″+45°24′35″;
(2) 79°45′+61°48′49″;
(3) 62°24′17″×4;
(4) 102°43′÷3. 4. 计算:答案:(1)58°;(2)141°33′49″;(3)249°37′8″;
(4)34°14′20″.5.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.解:设∠COD=x,
∵∠AOC=60°,∠BOD=90°,
∴∠AOD=60°-x,
∴∠AOB=90°+60°-x=150°-x,
∵∠AOB是∠DOC的3倍,
∴150°-x=3x,解得x=37.5°,
∴∠AOB=3×37.5°=112.5°.6.如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
(2) 若∠BOC=90°,求∠AOE的度数.课堂小结角的比较角的平分线度量法叠合法角的运算加与减乘与除角的和差倍分关系角的计算
2. 理解角平分线和角的和、差、倍、分的意义及数量
关系,能够用几何语言进行相关表述,并能解答相
关问题. (重点、难点)
3. 会进行涉及度、分、秒的角度的计算. (重点、难点)
有一天学生张亮和王帅各带了一把折扇(如图所示),下面是他们的一段对话:
张:我的折扇张开大一些,所以我的折扇的角也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.导入新课情境引入同学们,你们有办法帮他们进行判断吗?ABCDEF怎样比较∠ABC和∠DEF的大小?线段长短的比较AB>CDAB
AC=AB-BC线段的和、差线段中点若点 C 是线段 AB 的中点,则讲授新课 类比线段长短的比较,你认为该如何比较两个角的大小?1. 度量法类比探究2. 叠合法想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )∠AOB<∠A'O'B'∠AOB =∠A'O'B'∠AOB>∠A'O'B'图中有几个角?它们之间有什么关系?图中有3个角:∠AOC,∠AOB,∠BOC.∠AOC 是∠AOB 与∠BOC的和,记作∠AOC = ∠AOB +∠BOC;它们的关系:∠AOB 是∠AOC与∠BOC的差,记作∠AOB = ∠AOC-∠BOC;类似地,∠AOC-∠AOB= .观察与思考∠BOC练一练如图所示:
(1) ∠AOC是哪两个角的和?
(2) ∠AOB是哪两个角的差?
(3) 如果∠AOB=∠COD,则∠AOC与∠BOD
的大小关系如何?∠AOC =∠AOB +∠BOC.∠AOB =∠AOC -∠BOC =∠AOD-∠BOD.∠AOC =∠BOD.例1 如图,O 是直线 AB 上一点,∠AOC=53°17′,
求∠BOC 的度数.解:∵∠AOB 是平角,
∠AOB= ∠AOC+∠BOC.∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.典例精析(2) 如图②,若∠AOB= 60°,∠BOC=40°,则
∠AOC= °.
(1) 如图①,若∠AOC=35°,∠BOC=40°,则
∠AOB= °. 7520图① 图②变式训练(3) 若∠AOB =60°,∠AOC =30°,则∠BOC
= °. 90或30提示:无图条件下要分情况讨论. 如图,借助一副三角尺可以画出15°和75°的角,你还能画出哪些度数的角?试一试:75°15°例2 把一个周角 7 等分,每一份是多少度的角 (精确到分)?解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.(1) 120°-38°41′; (2)67°31′+48°49′. 解:原式 = 119°60′-38°41′
= 81°19′ .解:原式 = (67+48)°+(31+49)′
= 115°97′
= 116°37′ .变式训练计算方法总结:涉及到度、分、秒的角度的加与减,要将度与度、分与分、秒与秒分别相加、减,分秒相加时逢60要进位,相减时要借1作60.练一练1. 20°30′×8; 2. 106°6′÷5. 解:原式 = (106÷5)°+(6÷5)′= 21°+1°÷5
+(6÷5)′= 21°+(66÷5)′=21°+13′+1′÷5
=21°+13′+60″÷5=21°13′12″解:原式 = 20°×8+30′×8
= 160°240′
= 164°互动探究 动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:∠AOC_____∠COB;∠AOB=_____∠AOC.=2 一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线. 应用格式:OBAC∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.例3 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?解:因为 OB 平分∠AOC,
∠AOC=80°,(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD
是多少度?
解:因为 OB 平分∠AOC,所以 ∠BOC=∠AOB = 40°.因为 OD 平分∠COE,所以∠COD=∠DOE = 30°,所以
∠BOD =∠BOC+∠COD = 40°+30°= 70°.(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB
是多少度?解:因为 ∠COD=30°,
OD 平分∠COE,所以 ∠COE=2∠COD=60°,所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.又因为 OB 平分∠AOC,例4 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3.求OC与∠AOB的平分线所成的角的度数.解:分以下两种情况: 设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,∴2x+3x=40°,得x=8°,
∴∠AOC=2x=2×8°=16°.
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOD-∠AOC=20°-16°=4°. ?如图,OC在∠AOB内部,OD平分∠AOB,∴设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,
∴3x-2x=40°,得x=40°,
∴∠AOC=2x=2×40°=80°,
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOC+∠AOD=80°+20°=100°.
?如图,OC在∠AOB外部,OD平分∠AOB,∴OC与∠AOB的平分线所成的角的度数为4°或100°.方法总结:涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想和分类讨论思想解决问题.1. 如图:OC是∠AOB的平分线,OD是∠BOC的平
分线,那么下列各式中正确的是 ( )
A做一做2. 如图,OC是平角∠AOB的角平分线,∠COD=32°,
求∠AOD的度数.答案:∠AOD=122°.当堂练习1. 如图,∠AOB=∠COD=90,∠AOD=146°,则
∠BOC=____.2. 已知∠AOB=38°,∠BOC=25°,那么∠AOC
的度数是 .
34°13°或63°3. 如图,∠AOB=170°,∠AOC =∠BOD=90°,求∠COD的度数
答案:∠COD=10°.(1) 12°36′56″+45°24′35″;
(2) 79°45′+61°48′49″;
(3) 62°24′17″×4;
(4) 102°43′÷3. 4. 计算:答案:(1)58°;(2)141°33′49″;(3)249°37′8″;
(4)34°14′20″.5.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.解:设∠COD=x,
∵∠AOC=60°,∠BOD=90°,
∴∠AOD=60°-x,
∴∠AOB=90°+60°-x=150°-x,
∵∠AOB是∠DOC的3倍,
∴150°-x=3x,解得x=37.5°,
∴∠AOB=3×37.5°=112.5°.6.如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
(2) 若∠BOC=90°,求∠AOE的度数.课堂小结角的比较角的平分线度量法叠合法角的运算加与减乘与除角的和差倍分关系角的计算
