古埃及的数学 教案 (5)

古埃及的数学——尼罗河
教学目标分析：
1、了解古埃及数学的成就。
2、通过实例，感知并体会古埃及数学在实际生活中的应用。
3、激发学生的学习热情，激发学生的求知欲，培养严谨的学习态度，培养积极进取的精神
重难点分析：
重点： 了解古埃及数学的成就
难点： 理解古埃及数学加法运算、单位分数运算。
教学准备：多媒体课件
教学过程：
一、知识讲解：
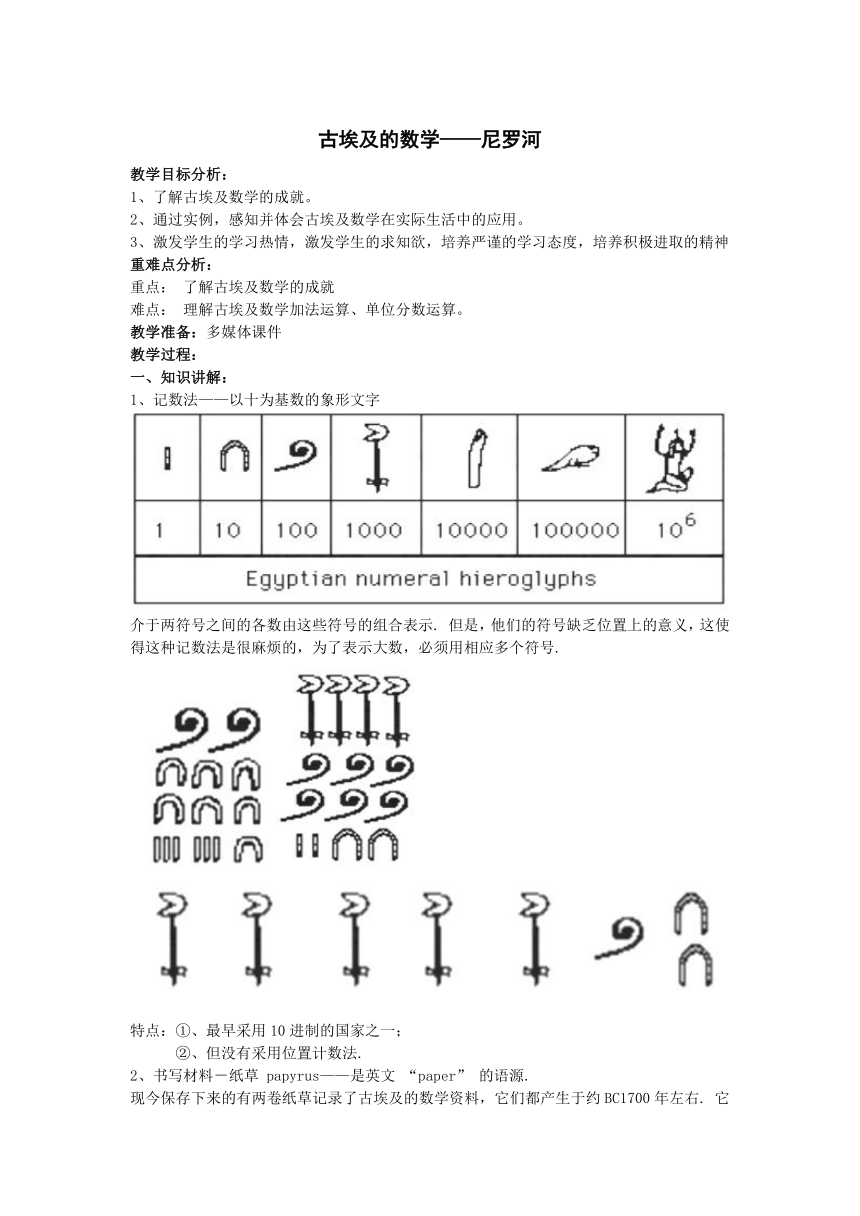
1、记数法——以十为基数的象形文字
介于两符号之间的各数由这些符号的组合表示. 但是，他们的符号缺乏位置上的意义，这使得这种记数法是很麻烦的，为了表示大数，必须用相应多个符号.
特点：①、最早采用10进制的国家之一；
②、但没有采用位置计数法.
2、书写材料－纸草 papyrus——是英文 “paper” 的语源.
现今保存下来的有两卷纸草记录了古埃及的数学资料，它们都产生于约BC1700年左右. 它们的作者可能是政治机关或教堂的书记（秘书），它们的内容就是题集和解答.
古埃及纸草书卷：
①莫斯科纸草(Moscow Papyrus)
（现存于莫斯科美术博物馆，一说现存于莫斯科普希金精细艺术博物馆）——25个数学问题（俄国贵族戈兰尼采夫于1893年在埃及发现），长约525cm，宽约8cm，成书于约BC1890年.
②兰德纸草(Rhind Papyrus)
（大英博物馆）——85个数学问题. 最初发现于埃及的底比斯古都废虚. （苏格兰人兰德 H. Rhind 于1858年购买于埃及），长约525cm，宽约33cm.
3、古埃及的算术知识：
（1）古埃及人的计算具有迭加的特点：任何自然数都可由2的各次幂的和组成.
例如： 计算 27×31
例：计算745÷26，只要连续地把除数26加倍，直到再加倍就超过745为止.
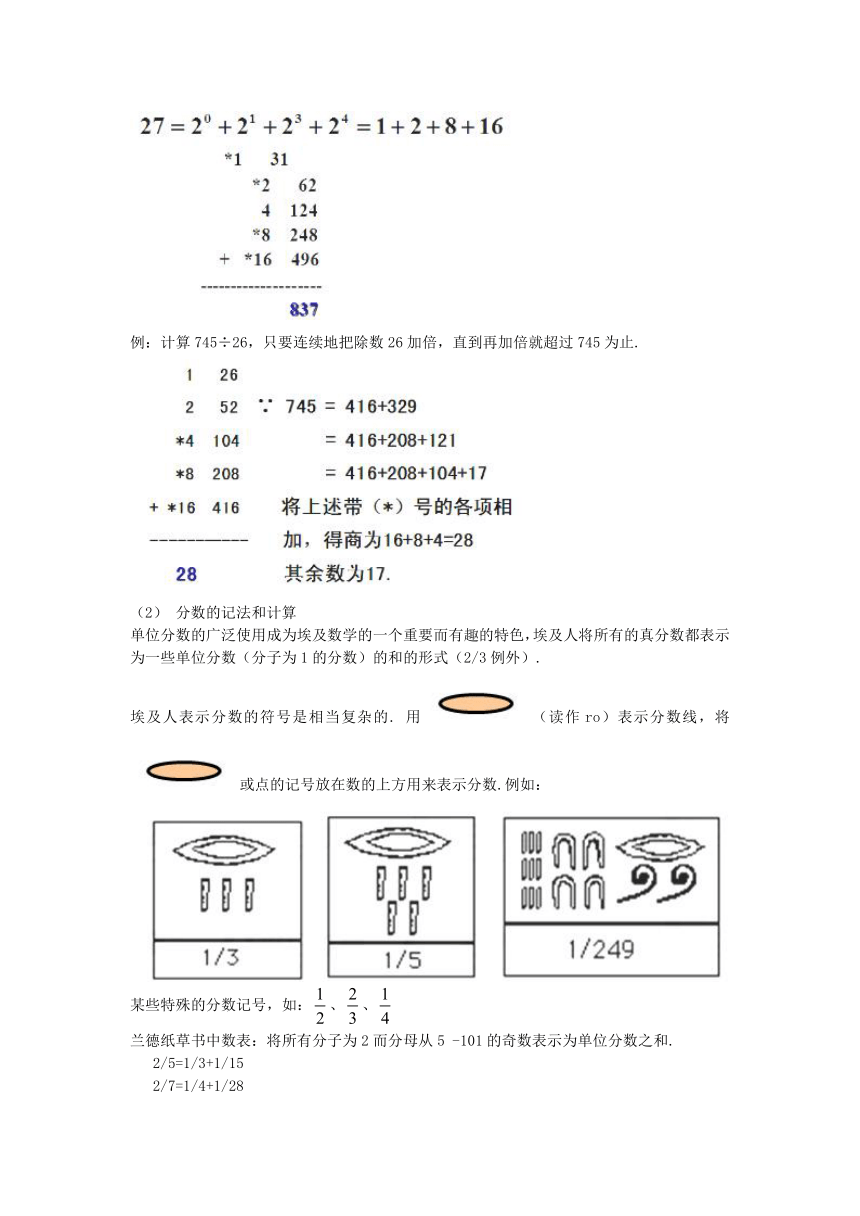
（2） 分数的记法和计算
单位分数的广泛使用成为埃及数学的一个重要而有趣的特色，埃及人将所有的真分数都表示为一些单位分数（分子为1的分数）的和的形式（2/3例外）.
埃及人表示分数的符号是相当复杂的. 用（读作ro）表示分数线，将或点的记号放在数的上方用来表示分数.例如：
某些特殊的分数记号，如：、、
兰德纸草书中数表：将所有分子为2而分母从5 -101的奇数表示为单位分数之和.
2/5=1/3+1/15
2/7=1/4+1/28
2/9=1/6+1/18
......
2/97=1/56+1/679+1/776
2/99=1/66+1/198
2/101=1/101+1/202+1/303+1/606
利用此表可进行分数计算
例如，要用5÷21，可写成单位分数之和
运算程序如下：
5/21=1/21+2/21+2/21
=1/21+1/14+1/42+1/14+1/42
=1/21+2/14+2/42
=1/21+1/7+1/21
=1/7+2/21
=1/7+1/14+1/42
? 注意：加倍程序和单位分数概念
兰德纸草书第70题：
求100÷(7+1/2+1/4+1/8)的商.
答：12+2/3+1/42+1/126.
解：将除数逐渐加倍：
15+1/2+1/4→31+1/2→63，是除数的8倍;
另外，除数与8+4+2/3相乘得 ，
比被除数100小1/4.
调整：因除数的8倍是63，故
(7+1/2+1/4+1/8)×2/63=1/4
由2/n数表查得
2/63=1/42+1/126，
于是
100÷(7+1/2+1/4+1/8)
= 8+4+2/3+2/63
= 12+2/3+1/42+1/126.
埃及人为什么对单位分数情有独钟，原因尚不清楚.
这种运算方法冗长繁复妨碍了数学的进一步发展，这也是古埃及算术和代数不能发展到更高水平的原因之一.
但是这种方法对于解决食物分配和土地分配问题却十分方便.
例如，平均分食物的7个面包8个人分.
7/8 = 1/2+1/4+1/8
（3）、完成了基本的算术四则运算
（4）、已经有了求近似平方根的方法
4、古埃及的代数：
①、有渐进的代数，但叙述方式是文词（即文词代数阶段），很少引用符号；
②、比例的概念也已有萌芽；三角函数观念的萌芽
③、一元一次方程求解
即形如：或某些二次方程：
④、等差级数和等比级数的概念及其求和
? 例1、兰德纸草书中有一方程问题：有一数量，它的2/3加它的1/2，加它的1/7，再加全部共为33.
用现代的记号是：
只不过分数部分写为
28/97=1/4+1/97+1/56+1/679+1/776+1/194+1/388.
古埃及人把未知数称为“堆”（aha)
例2、兰德纸草书中的第24题：已知“堆”与七分之一“堆”相加为19，求“堆”的值.
“假位法”（method of false position）—先假设一个特殊的数作为“堆”的值（多半是假值），将其代入等式左边去运算，然后比较得数与应得的结果，再通过比例的方法算出正确的答案.
在上例中，用数7作为未知数x的实验值，于是有，左边=
而应得的结果是19，这两个结果之比为19/8=2+1/4+1/8，将7乘以（2+1/4+1/18）即得正确的“堆”值为16+1/2+1/8.
例3、算术级数问题：5个人分100个面包，要求每个人所得的份数构成一个算术级数，并且前三个所得总数的1/7等于后二人所得之和---下伪法（regula falsi）
解： 先令第一项最大，这使得公差是负数.令首项和公差分别为a和d,写出了
于是公差为最小项的11/2倍，设最小项为1.
于是得级数：
但和为60,为满足条件，各项×5/3，
最后得：
例4、几何级数（等比级数）.兰德纸草书第79题：是在数字 7，49，343，2401，16807 旁边各注有图人，猫，鼠，大麦，量器等字样，而且给出总数为19607.
问这个题目产生的是什么数列？总数是多少？---有答案无解法.
“出门望九堤，堤有九木，木有九巢，巢有九鸟，鸟有九毛，毛有九色.”
5、古埃及的几何：
在兰德纸草书和莫斯科纸草书中确实包含有许多几何性质的问题，内容大都与土地面积和谷堆体积的计算有关.
由此可知，古埃及的几何很发达. 几何问题多是讲度量法，涉及到田地的面积，谷仓的容积和有关金字塔的计算等. 著名的“金字塔之迷”就是其中的代表.
（1）、法老胡夫的金字塔(Pyramid)：
兴建于齐阿斯王朝（BC2900年左右），高146.5米，塔基宽 233米，底边长度的误差为1.6厘米，正方程度与水平程度的平均误差≤1/10000，塔高与塔基之比非常近似于圆的周长与其半径之比.用以砌塔的巨石达230万块，重量从2.5吨到50吨不等.如把这些石头凿成平均一立方英尺的小块并排列成行，其长度相当于地球周长的2/3. 10万人用了20年的时间才建成的.
（2）、阿蒙神庙(Oman Tamples)：阿蒙——埃及的太阳神.王殿总面积5000平方米，有134根圆柱，中间最高的12根高达21米.
①、正方形,矩形,三角形,梯形面积公式.其他几何图形近似计算. 如：任意四边形的面积
②、已经知道毕达哥拉斯定理的特殊情况.
③、圆的面积很好的近似.
Rhind 50:假设一直径为9的圆形土地，其面积=边长为8的正方形土地.
由此可知，圆面积为 ，其中 d 为直径，相当于取π=3.1605，误差为0.6%.
④、体积的计算
正四棱台的体积－最高成就.
直棱柱(圆柱)的体积等于底面积乘以高.
⑤、半球表面积的计算公式.
⑥、知道相似三角形.
⑦、在求圆面积以及把圆分为若干相等部分的问题上，已经有了正确的知识.
二、问题探究：
1、古埃及数学有哪些内容？
2、古埃及的加法运算和单位分数运算与如今的计算方法有什么区别？
3、古埃及的面积、体积算法有什么特点？
小结反思：
静止的特性---产生于约BC1700年左右的兰德纸草书和莫斯科纸草书中的数学，在数千年漫长的岁月中很少变化.
加法运算和单位分数始终是埃及算术的砖块，使古埃及人的计算显得笨重繁复.
古埃及人的面积、体积算法对精确的公式和近似关系往往不作明确的区分，这又使他们的实用几何带上了粗糙的色彩.
公元前四世纪希腊人征服埃及以后，这一古老的数学文化完全被蒸蒸日上的希腊数学所代替
课外作业：
（1） 金字塔之谜
（2）普林斯顿第322号泥版
（3）古埃及的几何知识