古埃及的数学 课件 (2)

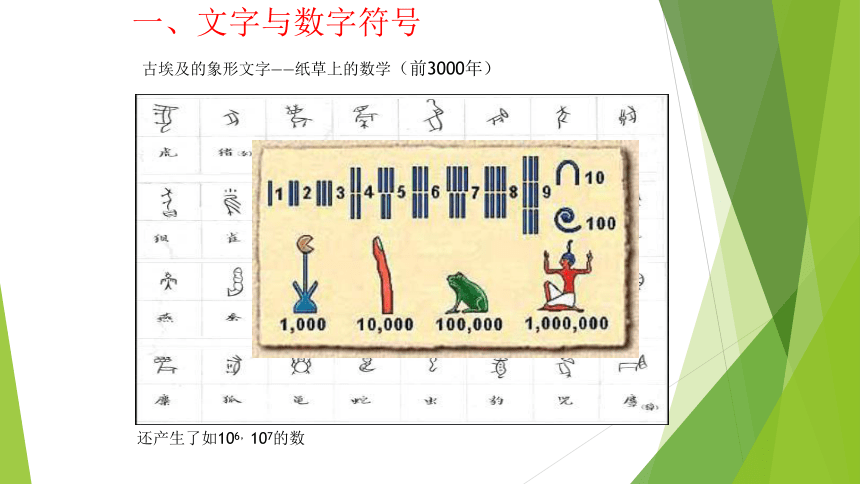
课件12张PPT。古埃及的数学一、文字与数字符号古埃及的象形文字——纸草上的数学（前3000年）还产生了如106，107的数纸草书上的数学纸草书 莫斯科纸草书（约公元前１６５０）
　莱因德纸草书（约公元前1８５0年）二、分数与小数：①莫斯科纸草(Moscow Papyrus)
（现存于莫斯科美术博物馆，一说现存于莫斯科普希金精细艺术博物馆）——25个数学问题（俄国贵族戈兰尼采夫于1893年在埃及发现），长约525cm，宽约8cm，成书于约BC1890年. ②莱因德纸草书(Rhind Papyrus)
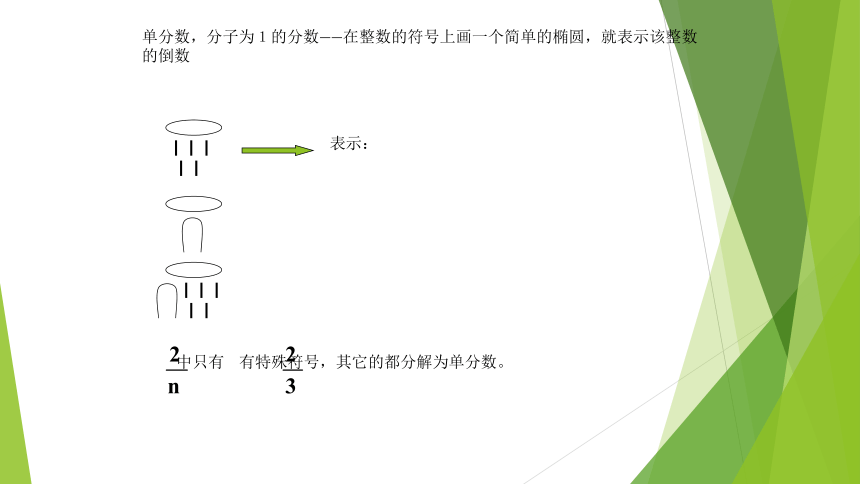
（大英博物馆）——85个数学问题. 最初发现于埃及的底比斯古都废虚. （苏格兰人兰德 H. Rhind 于1858年购买于埃及），长约525cm，宽约33cm.单分数，分子为１的分数——在整数的符号上画一个简单的椭圆，就表示该整数的倒数 中只有 有特殊符号，其它的都分解为单分数。三、进位制十进制四、算术运算纸草上的数学：分级记数法（古埃及僧侣文记数）整数加减法很方便，分数较复杂，要化为单分数。乘法是累加法（倍乘）。乘法：26X3326=2+8+16
26X33=66+264+528=858除法：19 ÷819=16+2+1
19 ÷8=2+1/4+1/8
五.代数纸草上的数学：下一量加上它自身的七分之一等于19.试位法例：X+X/7=24解：先给X选一个数值，比如令X=7于是7+7/7=8 ≠24因为8x3=24所以 X=7x3=21小结1、埃及人是惊人的创造者，他们创造数学的能力是难以置信的。对我们来说，他们揭示了几何和数学的威力，实现了令人兴奋的数学发现第一步。
2、古埃及记数系统的缺陷：是叠加制而不是位值制.谢谢观赏!