古希腊数学 课件 (2)

课件107张PPT。古代希腊数学
古代希腊数学地理历史概况

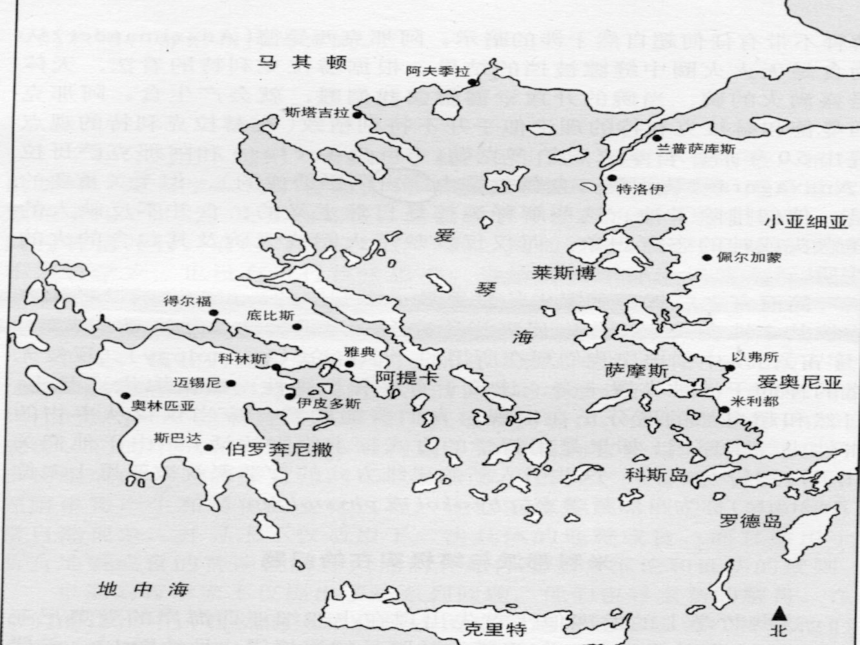
地理范围：
希腊半岛、原南斯拉夫、保加利亚南部、意大利半岛、土耳其及非洲北部

时间跨度：BC 600 至 600
古希腊的变迁雅典时期：公元前6－前3世纪公元前11世纪－前9世纪：希腊各部落进入爱琴地区
公元前9－前6世纪：希腊各城邦先后形成亚历山大后期：公元前30年－公元640年西罗马帝国：公元395年－公元476年
东罗马帝国：公元395年－公元1453年（610年改称拜占廷帝国）爱奥尼亚时期：公元前11世纪－前6世纪亚历山大时期：公元前323年－前30年罗马帝国：公元前27年－公元395年希腊时期希腊化时期波希战争（前499－前449）数学作为一门有组织、独立的和理性的学科来说，在古希腊学者登场之前是不存在的。
---M·克莱因 古代希腊数学一、希腊的先行者
二、毕达哥拉斯学派
三、欧几里得与《原本》
四、数学之神—阿基米得 古代希腊数学 一、希腊的先行者
——泰勒斯一、古希腊数学的先行者——伊奥尼亚学派创始人
古希腊最早的数学家、哲学家
“希腊七贤”之首泰勒斯最先证明了如下的定理:
1.两直线相交，对顶角相等。
2.等腰三角形两底角相等。
3.圆被直径二等分。
4.半圆上的圆周角是直角。
----泰勒斯定理
5.两个三角形全等的边角边定理。从泰勒斯开始，命题证明成为希腊数学的基本精神。泰勒斯(BC625—BC547)关于泰勒斯的传说早年经商，因垄断榨油设备发财
在埃及，利用立竿的影长测量过金字塔的高
在巴比伦，接触了当地的天文表和测量仪器成功预报了BC585年的一次日蚀埃及的金字塔 精于哲学、数学、天文学 和音乐理论二、毕达哥拉斯（Pythagoras）
约公元前580—前500年
希腊论证数学的另一位祖师 毕达哥拉斯学派创始人 信奉“万物皆数”费洛罗斯曾说:“人们所知道的任何事物都包含数。因此，如果没有数就既不可能表达，也不可能理解任何事物。”毕达哥拉斯（Pythagoras）毕达哥拉斯学派的主要成就勾股定理（毕达哥拉斯定理）
勾股数
正多面体
黄金分割
数的“理论”
不可公度量1．勾股定理（毕达哥拉斯定理） 毕达哥拉斯学派的主要成就：毕氏学派百牛大祭
法 国——驴桥问题
中 国----商高定理毕达哥拉斯定理（希腊，1955）.毕达哥拉斯学派的主要成就2. 勾股数（Pythagorean triple）
毕达哥拉斯学派的主要成就3. 正多面体
正四面体
正六面体
正八面体
正十二面体
正二十面体
其中正十二面体由正五边形围成，而正五边形的作图与著名的“黄金分割”有关毕达哥拉斯学派的主要成就：4.黄金分割
正五边形的五条对角线分别相交，这些交点以一种特殊的方式分割对角线：每条对角线都被交点分成两条不等的线段，使得

这就是所谓“黄金分割”.
www.mcs.surrey.ac.uk/Personal/R.Knott/
Fibonacci/fib.html
1Prof. Dr. rer. nat. Klaus-Dieter Graf jthe divine rectangle1Prof. Dr. rer. nat. Klaus-Dieter Graf divina proportione(divine proportion)golden sectionV I P jsolution:a-bthe golden section of a:condition:b数学与美学（黄金分割） 蝴蝶身长与双翅展开后的长度之比， 普通树叶的宽与长之比也接近0.618。数学与美学（黄金分割） 北纬30度有关的地方，奇石异峰，名川秀水的黄山，庐山，九寨沟等等。中国三大淡水湖也恰好在这黄金分割的纬度上。数学与美学（黄金分割） 雕塑断臂女神维纳斯的体型完全与黄金比相符，即以人的肚脐为分界点，上身与下身之比，或者说下身与全身之比约是0.618数学与美学（黄金分割） 蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割建筑中的黄金分割 东方明珠塔，塔高462.85米。设计师将在295米处设计了一个上球体埃菲尔铁塔埃及的金字塔金字塔底面的边长与高之比都接近于0.618.1Prof. Dr. rer. nat. Klaus-Dieter Graf Pyramidseb eb= j毕达哥拉斯学派的主要成就：5.数的“理论”
对数的“看法”
完全数
亲和数
形数毕达哥拉斯学派的主要成就5. 数的“理论”
（1）对数的“看法”
万物皆数
1称为“原因数”
10是最神圣的数
偶数是阴性的 奇数是阳性的
5是结婚的“象征”
讨厌17毕达哥拉斯学派的主要成就5. 数的“理论”
（2）完全数
毕派定义了“完全数”、“过剩数”与“不足数”
所谓完全数是指一个数的所有真因数之和恰好等于该数
换言之，一个数的所有因数之和恰好等于该数的两倍，则该数称为完全数毕达哥拉斯学派的主要成就5. 数的“理论”
（2）完全数
尼科马霍斯（AD100，约旦，其深受毕派影响）发现：
毕达哥拉斯学派的主要成就5. 数的“理论”
（2）完全数
事实上，现有定理：
毕达哥拉斯学派的主要成就5. 数的“理论”
（2）完全数
现己发现了47个M素数（见www.mersenne.org），即己发现47个完全数，其中最大的一个完全数（对应发现的第45个M素数）是：
毕达哥拉斯学派的主要成就5. 数的“理论”
（3）亲和数
若 a 的真因数之和等于 b，且 b 的真因数之和又等于 a，则称a，b为一对亲和数.
换言之：a 的所有因数之和
= b的所有因数之和
=a+b

毕达哥拉斯学派的主要成就5. 数的“理论”
（3）亲和数
亲和数的一个公式：

毕达哥拉斯学派的主要成就：
5. 数的“理论” （4）形数?毕达哥拉斯学派的主要成就：5. 数的“理论” （4）形数 形数（figured numbers）理论可以上溯到毕达哥拉斯（Pythagoras, 569 B.C.～500 B. C.）本人。用一点（或一个小石子）代表1，两点（或两个小石子）代表2，三点（或三个小石子）代表3，等等，毕达哥拉斯学派在世界数学史上首次建立了数和形之间的联系。早期毕达哥拉斯学派似乎已经熟悉利用小石子或点来构造三角形数和正方形数；晚期的毕达哥拉斯学派成员尼可麦丘（Nicomachus, 60?～120?）以及稍后的泰恩（Theon, 约2世纪上半叶）则讨论了各种平面数（包括三角形数、正方形数、长方形数、五边形数、六边形数等等）和立体数（包括立方数、棱锥数等等）。
（4）形数后期毕达哥拉斯学派数学家尼可麦丘在《算术引论》中将多边形数推广到立体数。前四个三棱锥数为

1 1+3 1+3+6 1+3+6+10（4）形数第n个三棱锥数为
（Nicomachus, 1世纪）（4）形数前四个四棱锥数为
1 1+4 1+4+9 1+4+9=16
第n个四棱锥数为
与形数有关的高考题2006年广东数学高考题
在德国不莱梅举行的第48届世乒赛期间，某商场橱窗里用同样的乒乓球成若干堆“正三棱锥”形的展品，其中第一堆只有一层，就一个球，第2、3、4 堆最底层（第一层）分别按图所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上，第 n 堆第 n 层就放一个乒乓球，以 f(n) 表示第 n?堆的乒乓球总数，则 f (3) =______， f (n) =______。 古希腊人常用小石子在沙滩上摆成各种形状来研究数，例如：

他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数;类似地，称图2中的1，4，9，16…这样的数成为正方形数。下列数中既是三角形数又是正方形数的是
A.289 B.1024 C.1225 D.1378 毕达哥拉斯学派的主要成就：
6.不可公度量万物皆数兴趣和实际应用若想预见数学的未来，正确的方法是研究它的历史和现状。
——H．彭加勒课后作业：1.查阅资料，了解第一次数学危机的背景、产生和解决；
2.查阅资料，了解勾股定理（毕达哥拉斯定理）的各种不同的证明方法；
3.查阅资料，了解各种不同的“形数” ，探究其中蕴含的关系。
无理数的发现──第一次数学危机
大约公元前５世纪，不可通约量的发现导致了毕达哥拉斯悖论。
第一次数学危机对古希腊的数学观点有极大冲击。这表明，几何学的某些真理与算术无关，几何量不能完全由整数及其比来表示，反之却可以由几何量来表示出来，整数的权威地位开始动摇，而几何学的身份升高了。危机也表明，直觉和经验不一定靠得住，.并由此建立了几何公理体系，这不能不说是数学思想上的一次巨大革命！ 无穷小是零吗？──第二次数学危机
18世纪，微分法和积分法在生产和实践上都有了广泛而成功的应用，大部分数学家对这一理论的可靠性是毫不怀疑的。贝克莱悖论。他指出：“牛顿在求xn的导数时，采取了先给x以增量０，应用二项式（x+0）n，从中减去xn以求得增量，并除以０以求出xn的增量与x的增量之比，然后又让０消逝，这样得出增量的最终比。这里牛顿做了违反矛盾律的手续──先设x有增量，又令增量为零，也即假设x没有增量。”他认为无穷小dx既等于零又不等于零，召之即来，挥之即去，这是荒谬，“dx为逝去量的灵魂”。无穷小量究竟是不是零？无穷小及其分析是否合理？由此而引起了数学界甚至哲学界长达一个半世纪的争论。导致了数学史上的第二次数学危机。 悖论的产生---第三次数学危机
数学史上的第三次危机，是由1897年的突然冲击而出现的，到现在，从整体来看，还没有解决到令人满意的程度。这次危机是由于在康托的一般集合理论的边缘发现悖论造成的。由于集合概念已经渗透到众多的数学分支，并且实际上集合论成了数学的基础，因此集合论中悖论的发现自然地引起了对数学的整个基本结构的有效性的怀疑。作业1 由欧几里得公式求出前五个完全数.
2 用亲和数公式求出两对亲和数黄金时代---亚历山大学派 BC 338-BC 30
北非 亚历山大城

欧几里得与几何《原本》
阿基米德的数学成就
阿波罗尼奥斯与《圆锥曲线论》 黄金时代---亚历山大学派三、 欧几里得与《原本》《原本》产生的历史背景
《原本》内容简介
《原本》存在的一些问题
2.2.1 欧几里得与《原本》欧几里德(约公元前300年，古希腊数学家)是古代希腊最负盛名、最有影响的数学家之一，他是亚历山大里亚学派的成员。编撰旷世巨著 ----《几何原本》(Elements)共有13卷。
这一著作对于几何学、数学和科学的
未来发展，对于西方人的整个思维
方法都有极大的影响。《几何原本》
的主要对象是几何学，
建立了第一个数学理论体系——
几何学。
标志着人类科学研究的公理化方法
的初步形成..一《原本》产生的历史背景
1 公理化思想己出现
2 毕派的“万物皆数”的影响
3 到BC 300，希腊数学己积累大 量知识
4 己有大量的前驱
工作，有同类著作
5 欧几里得的贡献二、《原本》内容简介 全书包括5条公理、5条公设、119个定义，证明了465个命题。
卷Ⅰ 三角形 垂直 平行 直线形
卷 Ⅱ 几何形式叙述代数问题
卷 Ⅲ、Ⅳ 有关圆的图形
卷 Ⅴ、Ⅵ 比例
卷 Ⅶ、Ⅷ、Ⅸ 正整数的性质
卷 Ⅹ 讨论不可公度量
卷 Ⅺ、Ⅻ、ⅩⅢ 立体几何
公设：
（1） 从任一点到任一点作直线是可能的。
（2） 把有限直线不断循直线延长是可能的。（注意，这里所谓的直线，相当于今天我们所说的线段。）
（3） 以任一点为中心和任一距离为半径作一圆是可能的。
（4） 所有直角彼此相等。
（5） 若一直线与两直线相交，且若同侧所交两内角之和小于两直角，则两直线无限延长后必相交于该侧的一点（现今称为平行公理）。《原本》的公理化体系：全书先给出若干条定义和公理，再按由简到繁的顺序编排出一系列的定理(465个命题)。使整个几何知识形成了一个演绎体系 公理：
（1） 跟一件东西相等的一些东西，它们彼此也是相等的。
（2） 等量加等量，总量仍相等。
（3） 等量减等量，余量仍相等。
（4） 彼此重合的东西是相等的。
（5） 整体大于部分。
从现代公理化方法的角度来分析，《原本》的公理化体系存在着以下一些缺陷：
没有认识到公理化的体系一定建立在一些原始概念上；
《原本》的公理集合是不完备的，这就使得欧几里得在推导命题过程中，不自觉地使用了物理的直观概念，但是建立在图形直观上的几何推理肯定是不可靠的.二、《原本》内容简介卷Ⅰ 首先给出23个定义：
1 点是没有部分的
2 线只有长度而没有宽度
3 一线的两端是点
……
然后是五个公设、五个公理.
公理之后给出48个命题，涉及三角形、垂直、平行、直线形等二、《原本》内容简介卷Ⅰ 命题47（毕达哥拉斯定理）
在直角三角形中，直角所对的边上的正方形等于夹直角两边上正方形的和.
卷Ⅰ 命题48（毕达哥拉斯定理的逆定理）
如果在一个三角形中，一边上的正方形等于这个三角形另外两边上正方形的和，则夹在后两边之间的角是直角.What does a proof “prove”?
What does it tell us?欧几里得的证明原图Henry Perigal
(1801-1898)A particularly neat transformation
of a2 and b2 into c2 This really shows the two squares on the
sides becoming the square on the hypotenuse二、《原本》内容简介卷Ⅱ 给出两个定义，14个命题，是用几何形式叙述代数问题，如：
卷Ⅱ 命题1 如果有两条线段，其中一条被截成任意几段，则原来两条线段所构成的矩形等于各个小段和未截线段构成的矩形之和.
卷Ⅱ 命题4 如果任意两分一个线段，则在整个线段上的正方形等于各个小段上的正方形的和加上两小段构成的矩形的二倍.二、《原本》内容简介卷Ⅲ 给出11个定义，37个命题，讨论圆、弦、切线、圆周角、圆内接四边形及有关圆的图形.
卷Ⅳ 给出7个定义，16个命题，包括圆内接三角形、圆外切三角形、正方形、圆内接正多边形的作图.
卷Ⅴ 给出18个定义，25个命题，讨论比例问题.
卷Ⅵ 给出4个定义，33个命题，是将卷Ⅴ的理论用到平面图形上.二、《原本》内容简介卷Ⅶ、卷Ⅷ、卷Ⅸ 分别有39、27、36个命题，讨论正整数的性质，如：
Ⅶ，32 任一数或者是素数，或者可被某数所量尽.
Ⅸ，20 预先给定任意多个素数，则有比它们更多的素数.Ⅸ，20 的证明欧几里得证明的现代叙述 库默尔（Kummer，1810----1893）在1878年给出欧几里得证明的一个巧妙变形： 美国数学月刊2006年10期发表了一个关于素数无限性简短证明 二、《原本》内容简介卷Ⅹ 讨论无理量，实际只涉及
共115个命题. 但卷Ⅹ命题1 十分重要.
Ⅹ，1 给定两个不相等的量，如果从较大量中减去大于其半的量，再从余下的量中减去大于其半的量，并且连续这样进行下去，则必得一个余量小于较小的量.二、《原本》内容简介卷Ⅺ、卷Ⅻ、卷ⅩⅢ 是立体几何，分别有39、18、18个命题.
其中卷Ⅻ详细陈述了“穷竭法”，它是古希腊数学家证明面积体积定理时常用的一种得力方法.可以卷Ⅻ命题2的证明过程为例说明其基本精神.
Ⅻ，1 圆内接相似多边形之比如同圆直径上正方形之比.
Ⅻ，2 圆与圆之比如同直径上正方形之比.
欧几里德的《原本》手稿失传
西方最早印刷教学书
----1842年《原本》印刷于意大利威尼斯
《原本》在西方流传仅次于《圣经》
中国的传入
----明末1606年徐光启，意大利传教士利玛窦共同翻译
三、《原本》存在的一些问题
1 有些定义不清
2 公理不完备
3 公理不独立
4 编排不统一
5 证明有时以偏概全作业
1 证明：卷Ⅰ 命题48（毕达哥拉斯定理的逆定理）
如果在一个三角形中，一边上的正方形等于这个三角形另外两边上正方形的和，则夹在后两边之间的角是直角.
四、 阿基米德的数学成就数学之神----阿基米德
阿基米德的主要著作
阿基米德的主要数学成就
2.2.2 阿基米德的数学成就一 数学之神-----阿基米德 BC287-BC212
公元前287年，阿基米德诞生于西西里岛的叙拉古(今意大利锡拉库萨)。他出生于贵族，与叙拉古的赫农王有亲戚关系，家庭十分富有。阿基米德的父亲是天文学家兼数学家，学识渊博，为人谦逊。他十一岁时，借助与王室的关系，被送到古希腊文化中心亚历山大
里亚城跟随欧几里得的学生学习、
以后与亚历山大的学者保持密切
联系。后世流传大量关于阿基米
德的传说，后人称他为有史以来
最伟大的三位数学家之首。
数学之神“给我一个支点，我就可以移动地球。”阿基米德(公元前287－前212年) (希腊, 1983)二 阿基米德的主要著作《圆的度量》；《抛物线求积》；《论螺线》；《论球和圆柱》；
《论辟锥曲面和旋转椭球》；
《引理集》； 《砂粒计数》；
《处理力学问题的方法》；
《论平面图形的平衡或其重心》；《论浮体》；《牛群问题》《圆的度量》一个直角三角形的两条直角边分别等于一个圆的半径和周长，则这个圆的面积和直角三角形的面积相等.
一个圆的面积与以圆的直径为边长的正方形的面积的比值恰好接近11：14.
圆的周长小于它的直径与 的乘积但大于它的直径乘以 的乘积.《论球和圆柱》
一个球体的体积，是一个以球体的大圆为底，以球体的半径为高的圆锥体积的四倍.《牛群问题》 太阳神在西西里岛上有一群牛，其中公牛、母牛，白、黑、花、棕四色俱全。在公牛中，白牛比棕牛多了黑牛数的二分之一又三分之一；黑牛比棕牛多了花牛数的四分之一又五分之一；花牛比棕牛多了白牛数的六分之一又七分之一。在母牛中，白牛是全部黑牛（包括公牛，下同）数的三分之一又四分之一；黑牛是全部花牛数的四分之一又五分之一；花牛是全部棕牛数的五分之一又六分之一；棕牛是全部白牛数的六分之一又七分之一。又全部黑、白公牛数的和是正方形数，全部花、棕公牛数的和是三角形数。问八种牛各有多少头？
三 阿基米德的主要数学成就
平衡法
穷竭法
阿基米德螺线
三 阿基米德的主要数学成就1 平衡法
为了求得一图形的面积或体积，首先将这个图形分成平行窄条或平行薄片，把分成的这些部分吊在一个给定的杠杆一端，使之同一个面积（或体积）和重心己知的图形相平衡.
例 “平衡法”推导球的体积公式案例 球体积公式阿基米德案例 球体积公式案例 球体积公式
AH : AT = 圆柱截面:（圆锥截面＋球截面）
(圆锥截面＋球截面) = 圆柱截面
(圆锥AEF＋球) = 圆柱EG， ???案例 球体积公式 球 = 4 圆锥ABD
? ? ? 案例 球体积公式
案例 球体积公式
球外切圆柱之表面积 ? ? 案例 球体积公式
? 与球体积有关的高考题半径为r的圆的面积S(r)＝ ,周长C(r)= ，若将r看作(0，＋∞)上的变量，则

（1）式可以用语言叙述为：圆的面积函数的导数等于圆的周长函数。对于半径为R的球，若将R看作(0，＋∞)上的变量，请你写出类似于（1）的式子： （2）
（2）式可以用语言叙述为： 。试题分析与球体积有关的高考题设球的半径为时间t 的函数R（t）。若球的体积以均匀速度C 增长，则球的表面积的增长速度与球半径
A.成正比，比例系数为C
B. 成正比，比例系数为2C
C.成反比，比例系数为C
D. 成反比，比例系数为2C 解析2010年高考数学湖北卷理13文14题 阿基米德的主要数学成就2 穷竭法
阿基米德用平衡法求出一个面积或体积后，必再用穷竭法给以严格的证明.这种发现与求证的双重方法，是阿基米德独特的思维方式.
这方面典型例子是抛物线弓形的求积.
用穷竭法计算平面图形面积. 阿基米德的主要数学成就3 阿基米德螺线
一条射线绕其固定端点匀速旋转，同时有一动点从端点出发沿射线匀速运动，那么这动点就描绘出一条平面螺线.

阿基米德探讨了螺线所围的面积，也研究了螺线的切线，给出作图方法及种种性质.
阿基米德螺线