毕达哥拉斯学派 课件 (2)

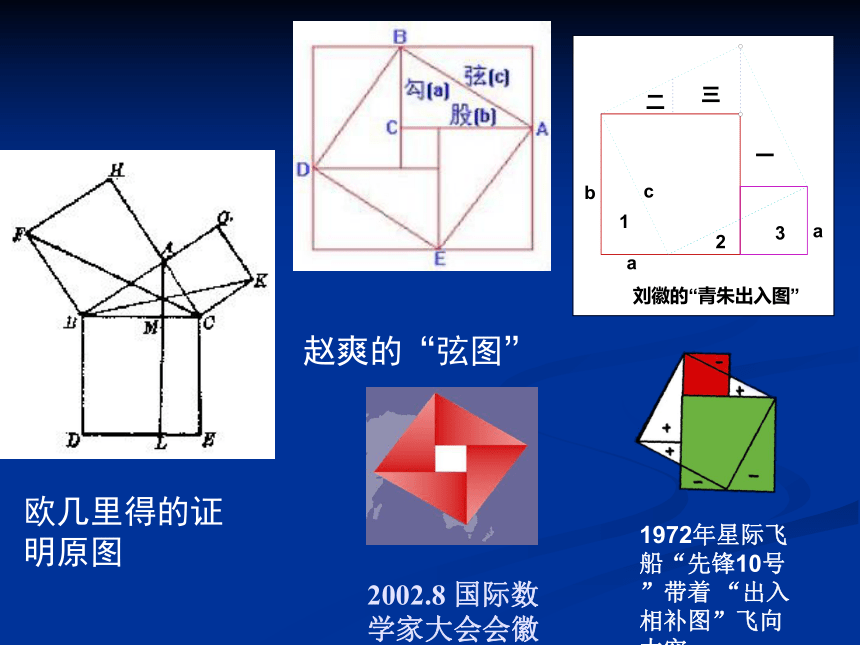
课件39张PPT。毕达哥拉斯（Pythagoras）毕达哥拉斯学派的主要成就勾股定理（毕达哥拉斯定理）
勾股数
正多面体
黄金分割
数的“理论”
不可公度量1．勾股定理（毕达哥拉斯定理） 毕达哥拉斯学派的主要成就：毕氏学派百牛大祭
法 国——驴桥问题
中 国----商高定理毕达哥拉斯定理（希腊，1955）.毕达哥拉斯学派的主要成就2. 勾股数（Pythagorean triple）
毕达哥拉斯学派的主要成就3. 正多面体
正四面体
正六面体
正八面体
正十二面体
正二十面体
其中正十二面体由正五边形围成，而正五边形的作图与著名的“黄金分割”有关毕达哥拉斯学派的主要成就：4.黄金分割
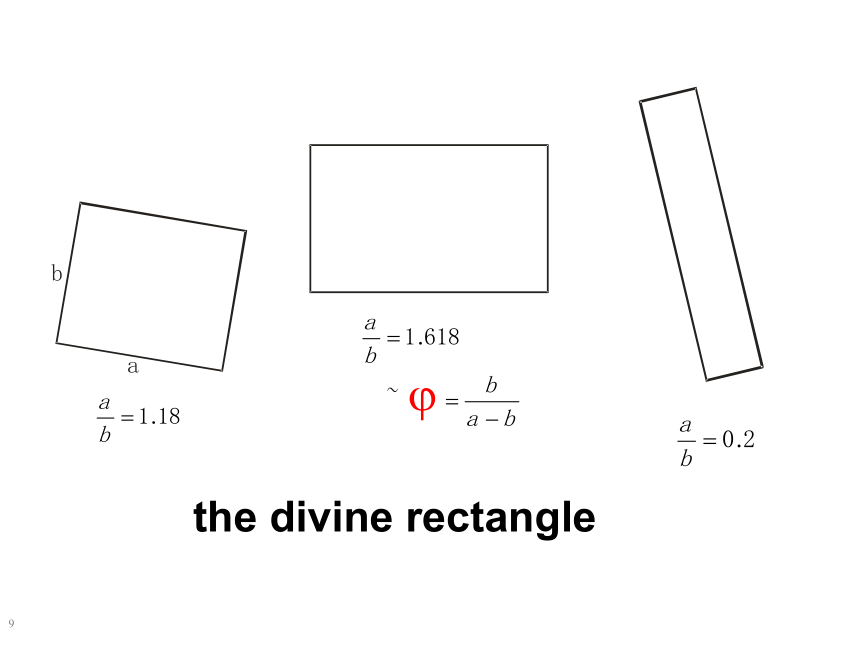
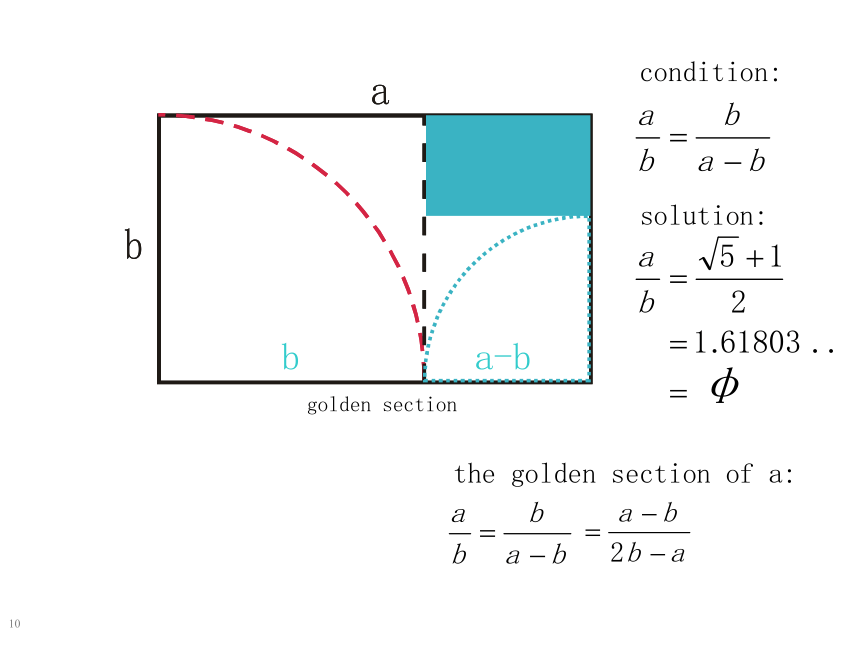
正五边形的五条对角线分别相交，这些交点以一种特殊的方式分割对角线：每条对角线都被交点分成两条不等的线段，使得

这就是所谓“黄金分割”.
1jthe divine rectangle1golden sectionsolution:a-bthe golden section of a:condition:b数学与美学（黄金分割） 蝴蝶身长与双翅展开后的长度之比， 普通树叶的宽与长之比也接近0.618。数学与美学（黄金分割） 北纬30度有关的地方，奇石异峰，名川秀水的黄山，庐山，九寨沟等等。中国三大淡水湖也恰好在这黄金分割的纬度上。数学与美学（黄金分割） 雕塑断臂女神维纳斯的体型完全与黄金比相符，即以人的肚脐为分界点，上身与下身之比，或者说下身与全身之比约是0.618数学与美学（黄金分割） 蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割建筑中的黄金分割 东方明珠塔，塔高462.85米。设计师将在295米处设计了一个上球体埃菲尔铁塔埃及的金字塔金字塔底面的边长与高之比都接近于0.618.1Prof. Dr. rer. nat. Klaus-Dieter Graf Pyramidseb eb= j例题讲解：解析毕达哥拉斯学派的主要成就：5.数的“理论”
对数的“看法”
完全数
亲和数
形数毕达哥拉斯学派的主要成就5. 数的“理论”
（1）对数的“看法”
万物皆数
1称为“原因数”
10是最神圣的数
偶数是阴性的 奇数是阳性的
5是结婚的“象征”
讨厌17毕达哥拉斯学派的主要成就5. 数的“理论”
（2）完全数
毕派定义了“完全数”、“过剩数”与“不足数”
所谓完全数是指一个数的所有真因数之和恰好等于该数
换言之，一个数的所有因数之和恰好等于该数的两倍，则该数称为完全数毕达哥拉斯学派的主要成就5. 数的“理论”
（3）亲和数
若 a 的真因数之和等于 b，且 b 的真因数之和又等于 a，则称a，b为一对亲和数.
换言之：a 的所有因数之和
= b的所有因数之和
=a+b

毕达哥拉斯学派的主要成就5. 数的“理论”
（3）亲和数
亲和数的一个公式：

毕达哥拉斯学派的主要成就：
5. 数的“理论” （4）形数?毕达哥拉斯学派的主要成就：5. 数的“理论” （4）形数 形数（figured numbers）理论可以上溯到毕达哥拉斯（Pythagoras, 569 B.C.～500 B. C.）本人。用一点（或一个小石子）代表1，两点（或两个小石子）代表2，三点（或三个小石子）代表3，等等，毕达哥拉斯学派在世界数学史上首次建立了数和形之间的联系。早期毕达哥拉斯学派似乎已经熟悉利用小石子或点来构造三角形数和正方形数；晚期的毕达哥拉斯学派成员尼可麦丘（Nicomachus, 60?～120?）以及稍后的泰恩（Theon, 约2世纪上半叶）则讨论了各种平面数（包括三角形数、正方形数、长方形数、五边形数、六边形数等等）和立体数（包括立方数、棱锥数等等）。
（4）形数后期毕达哥拉斯学派数学家尼可麦丘在《算术引论》中将多边形数推广到立体数。前四个三棱锥数为

1 1+3 1+3+6 1+3+6+10（4）形数第n个三棱锥数为
（Nicomachus, 1世纪）（4）形数前四个四棱锥数为
1 1+4 1+4+9 1+4+9=16
第n个四棱锥数为
与形数有关的高考题在德国不莱梅举行的第48届世乒赛期间，某商场橱窗里用同样的乒乓球成若干堆“正三棱锥”形的展品，其中第一堆只有一层，就一个球，第2、3、4 堆最底层（第一层）分别按图所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上，第 n 堆第 n 层就放一个乒乓球，以 f(n) 表示第 n?堆的乒乓球总数，则 f (3) =______， f (n) =______。 古希腊人常用小石子在沙滩上摆成各种形状来研究数，例如：

他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数;类似地，称图2中的1，4，9，16…这样的数成为正方形数。下列数中既是三角形数又是正方形数的是
A.289 B.1024 C.1225 D.1378解析数论背景