毕达哥拉斯学派 学案 (2)

毕达哥拉斯学派
一、自学目标：通过自学本节内容了解毕达哥拉斯学派的数学成就。
二、自学内容提炼
（一）提出问题
1、毕达哥拉斯学派的数学成就有哪些？
2、辨析284和220是亲和数
（二）导入新知
1、 学派
与泰勒斯不同，毕达哥拉斯不是个商人而是个神秘主义者。与几何学相比，他对数更感兴趣，他的兴趣源于宗教信仰以及对数学的深信不疑。? 和泰勒斯一样，毕达哥拉斯年轻时游历广泛。到最终定居下来时，他成了一位被人们崇拜的人物。 毕达哥拉斯公元前580年左右生于萨摩斯(今希腊东部小岛)。为了摆脱暴政，移居意大利半岛南部的克罗顿。在那里组织一个政治、宗教、哲学、数学合一的秘密团体。后来在政治斗争中遭到破坏，毕达哥拉斯被杀害，但他的学派还继续存在两个世纪(约公元前500～前300)之久。 毕达哥拉斯非常重视数学，企图用数来解释一切。这个学派不仅仅认为万物都包含数，而且说万物都是数。这学派有一种习惯，就是一切发明都归功于学派的领认而且常常是秘而不宣。所以后人很难知道究竞是谁在什么时候发明的。
2、毕达哥拉斯学派的信条
毕达哥拉斯学派的信条是：“ ”。也就是说，数是万物的本源，这就是毕达哥拉斯学派的“数本说”。毕达哥拉斯学派有一句原话：“ 是人类思想的向导和主人，没有它的力量，万物就都处于昏暗混乱之中。” 该学派的一位晚期成员费罗斯（Philolaus）就曾宣称：“人们所知道的一切事物都包含数，因此，没有数就既不可能表达，也不可能理解任何事物。”当然，毕达哥拉斯所说的数仅指 ，分数是被看成两个 的比。“万物皆数”是历史上第一次用数来观察、解释世界的学说。
3、毕达哥拉斯定理
毕达哥拉斯本人发现人所共知的“ ”的时候，欢欣之情不可言状．传说还宰了一百头牲畜来祭缪斯女神(Muses，神话中掌管文艺、科学的女神)，以酬谢神的默示。 勾股定理早己为巴比伦人所知。不过最早的证明，大概还应归功于毕达哥拉斯学派，可惜证法已失传。现在教科书所采用的面积证法，如欧几里得《几何原本》卷1的47题，是欧儿里得首先给出。
4形数
形数（figured numbers）理论可以上溯到毕达哥拉斯（Pythagoras, 569 B.C.～500 B. C.）本人。用一点（或一个小石子）代表1，两点（或两个小石子）代表2，三点（或三个小石子）代表3，等等，毕达哥拉斯学派在世界数学史上首次建立了 和 之间的联系。早期毕达哥拉斯学派似乎已经熟悉利用小石子或点来构造三角形数和正方形数；晚期的毕达哥拉斯学派成员尼可麦丘（Nicomachus, 60?～120?）以及稍后的泰恩（Theon, 约2世纪上半叶）则讨论了各种平面数（包括三角形数、正方形数、长方形数、五边形数、六边形数等等）和立体数（包括立方数、棱锥数等等）。
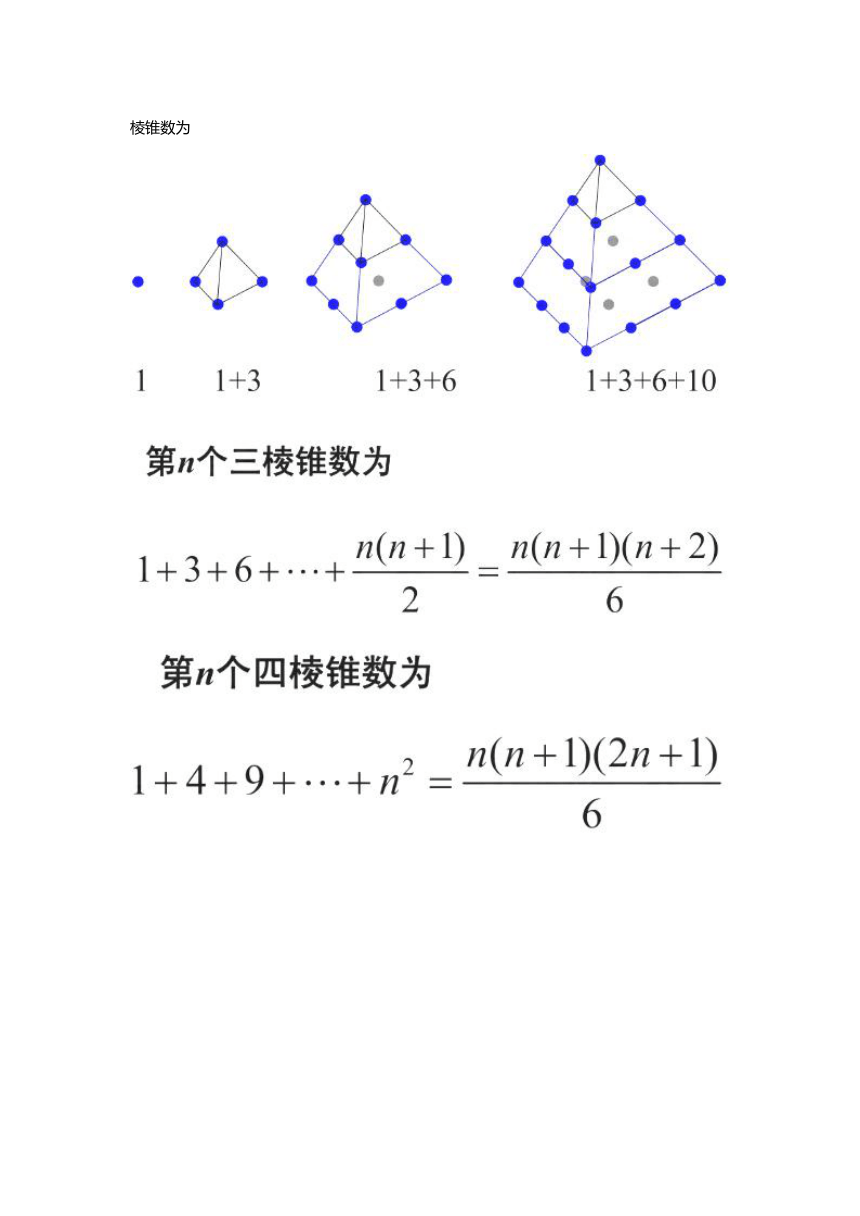
后期毕达哥拉斯学派数学家尼可麦丘在《算术引论》中将多边形数推广到立体数。前四个三棱锥数为
① 数：两个数是亲和的，即每一个数是另一个数的真因子的和。
好长一段时间再没有发现新的亲和数。直到1636年，费马宣布17296和18416为另一对亲和数。（只不过，这对亲和数在十三世纪末、十四世纪初曾被人发现过。）
又过了两年，笛卡尔给出了第三对。在1747年，欧拉给出了一个30对亲和数的表，后来又扩展到超过60对。
1886年，一个16岁的意大利男孩发现了被人们忽视的、比较小的一对亲和数：1184和1210。
现在已知道上千对亲和数。
② 数：如果一个数等于其真因子的和，则称为 数。例如，6=1+2+3。
直到 1952 年，才知道 12 个完全数，它们都是偶数，头三个是 6，28，496。 《原本》第九卷的最后一个命题：如果22-1是一个素数，则是一个完全数。
奇完全数的存在与否中数论中著名的未解决的问题之一。
③ 数：如果一个数大于其真因子的和，则称为 数。如8>1+2+4。
④ 数：如果一个数小于其真因子的和，则称 数。
求整数 a、b、c，要它们能表示一个直角三角形的三边，这三个数被称为 三数。普林顿 322 号的分析充分地证实，古代巴比伦人就知道如何计算这三个数。
一般认为，毕氏学派已发现了公式：
对于任何奇数，这三项就是毕氏三数。
⑤无理数
无理数的发现（第一次数学危机）的发现在毕氏学派中引起震惊。据说，毕氏学派的希帕苏斯（也许是别人），由于泄密被扔到海里；另一种说法是被毕氏开除出毕氏团体，把它当作死人，还为他建了一个墓。无理数的发现是毕达哥拉斯学派最卓越的功绩，也是整个数学史上一项重大发现。柏拉图认为，在知道这个概念（不可公度性的概念）之前，自己一直像动物一样生活——没有生活在理性之中。
无理性的几何证明
已知存在一条线段 AP ，使得正方形 ABCD 的对角线 AC 和边AB 均为 AP 的整数倍，即 AC 和 AB 对于 AP 是可通约的。
在 AC 上截取CB1 =AB =，并作B1C1 垂直于 CA ，易证：C1 B= B1C1= AB1 。于是，AC1= AB- AB 1和 AB1 对于 AP 可通约的。（ 注意：AB1= AC -AB ）
但是AC1 和AB 1是比原来那个正方形的一半还要小的正方形的对角线的边。从而，重复此过程，最终可以得到一个正方形，其对角线ACn 和边ABn 对于 AP 是可通约的，并ACn < AP ，矛盾。
（三）例题选讲
某商场橱窗里用同样的乒乓球成若干堆届世乒赛期间，某商场橱窗里用同样的乒乓球成若干堆“ 正三棱锥”形的展品，其中第一堆只有一层，就一个球，第形的展品，其中第一堆只有一层，就一个球，第2 、3 、4 堆最底层（第一层）分别按图所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上，第堆最底层（第一层）分别按图所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上，第 n 堆第 n以 层就放一个乒乓球，以 f(n) 表示第 n 堆的乒乓球总数，则堆的乒乓球总数，则 f (3) =______， f (n) =______
解：易知f（3）=10．
由题意知f（2）比f（1）多最底层：1+2（个），
f（3）比f（2）多最底层：1+2+3（个），
f（4）比f（3）多最底层：1+2+3+4（个），
…
f（n）比f（n-1）多最底层：1+2+3++n（个）
∴f（n）-f（n-1）=1+2+3+…+n=
∴由累加法可得f(n)＝
故答案为：10；
（四）化解疑难
1、毕达哥拉斯学派对数学贡献有哪些？
答：对“命题证明思想作”了巨大的推进，可以说是欧几里德公理化体系的先驱。他们研究数学 从这些实际应用中摆脱出来，把数学当作一种思想来追求，通过它去追求永恒的真理。
2、辨析284和220是亲和数？
解：220的真因子是1，2，4，5，10，20，22，44，55，110，其和为284；而284的真因子为1，2，4，71，142，其和为220。 故284和220是亲和数。