人教A版高中数学必修五3.4基本不等式(2)课件(共36张PPT)
文档属性
| 名称 | 人教A版高中数学必修五3.4基本不等式(2)课件(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-06 08:16:58 | ||
图片预览











文档简介
课件36张PPT。第2课时 基本不等式的应用 张先生打算建造一个面积为6 000平方米的矩形饲
养场,进行猪养殖,现在需要进行周边院墙的建
设,经过计算,他的
儿子说建成正方形的
院墙最省,而他认为
建成长300米、宽200
米的矩形的院墙最
省,你认为谁说的
对?要解决这个问题,
可用基本不等式来解决,这一节我们就学习基本不等
式的有关应用. 1.利用基本不等式解决简单的最大值、最小值问题.(重点)2.会合理拆项或凑项,会应用基本不等式.(重点)3.会求给定条件的最值问题.【解题关键】设矩形菜园的长为x m,宽为y m,
面积确定,则xy=100,篱笆的长为2(x+y)m.
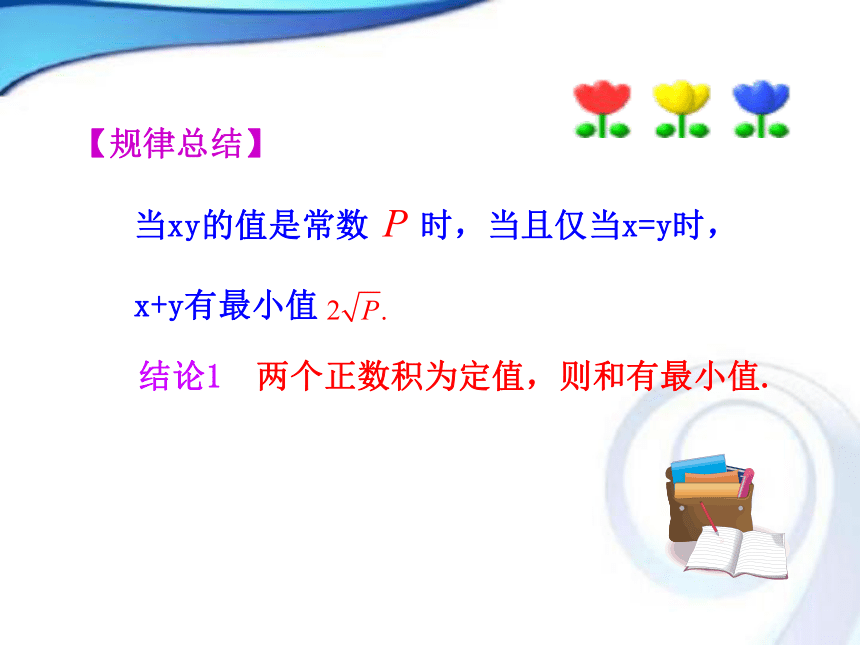
即求(x+y)的最小值.例1 (1)用篱笆围一个面积为100 m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短.最短的篱笆是多少?探究点1 基本不等式在求最值中的应用【解析】设矩形菜园的长为x m,宽为y m, 则xy=100,篱笆的长为2(x+y)m. 当且仅当x=y时等号成立,此时x=y=10. 因此,这个矩形的长、宽都为10 m时,所用篱笆最短,最短篱笆是40 m. 结论1 两个正数积为定值,则和有最小值.当xy的值是常数 时,当且仅当x=y时,
x+y有最小值【规律总结】【解题关键】设矩形菜园的长为x m,宽为y m,
周长确定,则2(x+y)=36,篱笆的面积为xy m2.即求xy的最大值.例1 (2)一段长为36 m的篱笆围成一个矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大.最大面积是多少?【解析】设矩形菜园的长为x m,宽为y m, 则 2(x + y)= 36, x+ y=18,矩形菜园的面积为xy m2 .当且仅当x=y=9时,等号成立.因此,这个矩形的长、宽都为9 m时,
菜园的面积最大,最大面积是81 m2 .结论2 两个正数和为定值,则积有最大值.当x+y的值是常数S时,当且仅当x=y时,
xy有最大值【提升总结】注意:①各项皆为正数;
②和为定值或积为定值;
③注意等号成立的条件.一“正”,
二“定”,
三“等”.最值定理结论1 两个正数积为定值,则和有最小值.结论2 两个正数和为定值,则积有最大值.【变式练习】【解题关键】把楼房每平方米的平均综合费用表示为楼房层数x的函数表达式。变形后利用基本不等式求最值。例2 某工厂要建造一个长方体形无盖贮水池,其容积为4 800 m3,深为3 m.如果池底每平方米的造价为150元, 池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?【解题关键】水池呈长方体形,高为3 m,底面的长与宽没有确定. 如果底面的长与宽确定了,水池总造价也就确定了.因此应当考察底面的长与宽取什么值时水池总造价最低.由容积为4 800 m3 ,可得3xy=4 800,因此xy=
1 600.由基本不等式与不等式的性质,可得【解析】设底面的长为x m,宽为y m,水池总造价为z元,根据题意,有 所以,将水池的底面设计成边长为40 m的正方形时总造价最低,最低总造价是
297 600元.【变式练习】C1.化正型探究点2 基本不等式在求最大、最小值中的应用【规律总结】如果所求因式都是负数,通常采用添负号变为正数的处理方法.关注因式是负数设函数 ,则函数f(x)的最大值
为_____。负变正【变式练习】2.凑定型(1)构造积为定值,利用基本不等式求最值.(2)构造和为定值,利用基本不等式求最值. 合理地拆分转化,构造和为定值或积为定值,并利用基本不等式的条件来求解,是解决此类问题的关键.【规律总结】有最小值1.【即时练习】例6 已知x>0,y>0,且2x+y=1,求 的最小值.3.整体代换型这个解法正确吗? 不正确.
过程中两次运用了基本不等式中取“=”过渡,而这两次取“=”的条件是不同的,故结果错误. 对于给定条件求最值的问题,常可采用乘“1”变换的方法,创造使用基本不等式的条件.【规律总结】【变式练习】范围是( )D1.若A.B.C.D.C45.x>0,y>0 且2x-8y-xy=0,求x+y的最小值。【解析】由题意得2x+8y=xy把握基本不等式成立的三个条件:
1.不具备“正值”条件时,需将其转化为正值.
2.不具备“定值”条件时,需构造定值条件.
(构造:互为相反数、互为倒数)
3.不具备“相等”条件时,需进行适当变形或利用函数单调性求值域.
养场,进行猪养殖,现在需要进行周边院墙的建
设,经过计算,他的
儿子说建成正方形的
院墙最省,而他认为
建成长300米、宽200
米的矩形的院墙最
省,你认为谁说的
对?要解决这个问题,
可用基本不等式来解决,这一节我们就学习基本不等
式的有关应用. 1.利用基本不等式解决简单的最大值、最小值问题.(重点)2.会合理拆项或凑项,会应用基本不等式.(重点)3.会求给定条件的最值问题.【解题关键】设矩形菜园的长为x m,宽为y m,
面积确定,则xy=100,篱笆的长为2(x+y)m.
即求(x+y)的最小值.例1 (1)用篱笆围一个面积为100 m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短.最短的篱笆是多少?探究点1 基本不等式在求最值中的应用【解析】设矩形菜园的长为x m,宽为y m, 则xy=100,篱笆的长为2(x+y)m. 当且仅当x=y时等号成立,此时x=y=10. 因此,这个矩形的长、宽都为10 m时,所用篱笆最短,最短篱笆是40 m. 结论1 两个正数积为定值,则和有最小值.当xy的值是常数 时,当且仅当x=y时,
x+y有最小值【规律总结】【解题关键】设矩形菜园的长为x m,宽为y m,
周长确定,则2(x+y)=36,篱笆的面积为xy m2.即求xy的最大值.例1 (2)一段长为36 m的篱笆围成一个矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大.最大面积是多少?【解析】设矩形菜园的长为x m,宽为y m, 则 2(x + y)= 36, x+ y=18,矩形菜园的面积为xy m2 .当且仅当x=y=9时,等号成立.因此,这个矩形的长、宽都为9 m时,
菜园的面积最大,最大面积是81 m2 .结论2 两个正数和为定值,则积有最大值.当x+y的值是常数S时,当且仅当x=y时,
xy有最大值【提升总结】注意:①各项皆为正数;
②和为定值或积为定值;
③注意等号成立的条件.一“正”,
二“定”,
三“等”.最值定理结论1 两个正数积为定值,则和有最小值.结论2 两个正数和为定值,则积有最大值.【变式练习】【解题关键】把楼房每平方米的平均综合费用表示为楼房层数x的函数表达式。变形后利用基本不等式求最值。例2 某工厂要建造一个长方体形无盖贮水池,其容积为4 800 m3,深为3 m.如果池底每平方米的造价为150元, 池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?【解题关键】水池呈长方体形,高为3 m,底面的长与宽没有确定. 如果底面的长与宽确定了,水池总造价也就确定了.因此应当考察底面的长与宽取什么值时水池总造价最低.由容积为4 800 m3 ,可得3xy=4 800,因此xy=
1 600.由基本不等式与不等式的性质,可得【解析】设底面的长为x m,宽为y m,水池总造价为z元,根据题意,有 所以,将水池的底面设计成边长为40 m的正方形时总造价最低,最低总造价是
297 600元.【变式练习】C1.化正型探究点2 基本不等式在求最大、最小值中的应用【规律总结】如果所求因式都是负数,通常采用添负号变为正数的处理方法.关注因式是负数设函数 ,则函数f(x)的最大值
为_____。负变正【变式练习】2.凑定型(1)构造积为定值,利用基本不等式求最值.(2)构造和为定值,利用基本不等式求最值. 合理地拆分转化,构造和为定值或积为定值,并利用基本不等式的条件来求解,是解决此类问题的关键.【规律总结】有最小值1.【即时练习】例6 已知x>0,y>0,且2x+y=1,求 的最小值.3.整体代换型这个解法正确吗? 不正确.
过程中两次运用了基本不等式中取“=”过渡,而这两次取“=”的条件是不同的,故结果错误. 对于给定条件求最值的问题,常可采用乘“1”变换的方法,创造使用基本不等式的条件.【规律总结】【变式练习】范围是( )D1.若A.B.C.D.C45.x>0,y>0 且2x-8y-xy=0,求x+y的最小值。【解析】由题意得2x+8y=xy把握基本不等式成立的三个条件:
1.不具备“正值”条件时,需将其转化为正值.
2.不具备“定值”条件时,需构造定值条件.
(构造:互为相反数、互为倒数)
3.不具备“相等”条件时,需进行适当变形或利用函数单调性求值域.
