人教A版高中数学必修五第三章复习小结课件(共33张PPT)
文档属性
| 名称 | 人教A版高中数学必修五第三章复习小结课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 413.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-07 10:08:14 | ||
图片预览








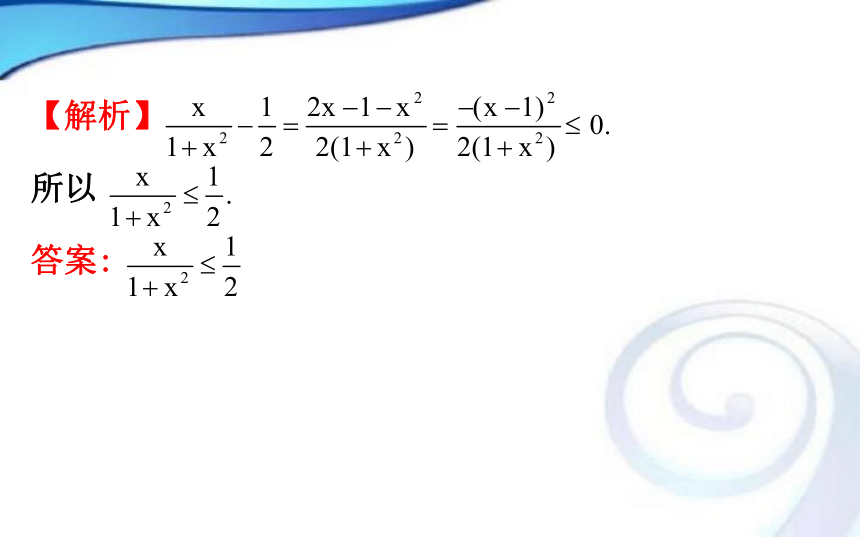


文档简介
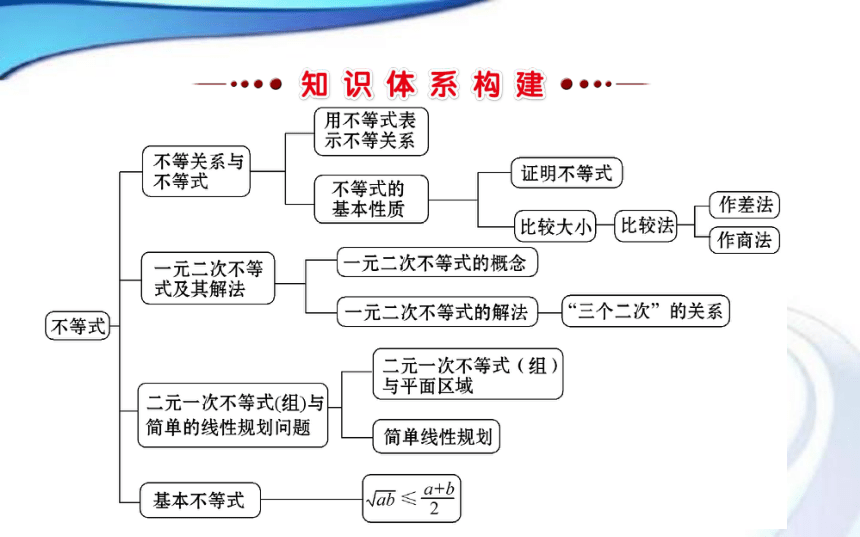
课件33张PPT。单元复习课
第三章类型一:不等关系与不等式的性质
【典例1】(1)下列结论正确的是 ( )
A.若ac>bc,则a>b
B.若a2>b2,则a>b
C.若a>b,c<0,则a+cD.若 ,则a0,b>0,且a≠b,比较 与a+b的大小.【解析】(1)选D.对于A项,考查的是不等式的性质,当c大于零时才行,所以A不对;对于B项,结论应该为|a|>
|b|,故B项是错的;对于C项,应该是不等式的两边同时加上一个数,不等号的方向不变,故C错;对于D项涉及不等式的乘方运算性质,只有D对.(2)因为
因为a>0,b>0,且a≠b,
所以(a-b)2>0,a+b>0,ab>0,
所以 即 >a+b.【规律总结】
1.比较大小的方法及步骤
(1)作差法,步骤如下:①作差;②变形;③判断差的符号;④结论.
(2)作商法,步骤如下:①作商;②变形;③判断商与1的关系;④结论.2.作差法及作商法的目的及适用类型
(1)目的:作差的目的是判断差的符号,而作商的目的是判断商与1的大小.两种方法的关键是变形,常用的变形技巧有因式分解、配方、有理化等.
(2)适用类型:当两个代数式的正负不确定且为多项式形式时,常用作差法比较大小,当两个代数式均为正且均为幂的乘积式时,常用作商法比较大小.【巩固训练】若x∈R,则 与 的大小关系为
________.【解析】
所以
答案: 类型二:不等式的解法
【典例2】(2016·遵义高二检测)若不等式(1-a)x2-4x+6>0的解集是{x|-3(1)解不等式2x2+(2-a)x-a>0.
(2)b为何值时,ax2+bx+3≥0的解集为R.【解析】(1)由题意知1-a<0,且-3和1是方程(1-a)x2-
4x+6=0的两根,故 即a=3,
原不等式?2x2-x-3>0?(x+1)(2x-3)>0
?x> 或x<-1.即原不等式的解集为
(2)因为3x2+bx+3≥0的解集为R,
所以Δ=b2-4×3×3≤0,故-6≤b≤6.【规律总结】一元二次不等式的解法
(1)一元二次不等式的解法
①将不等式化为ax2+bx+c>0(a>0)
或ax2+bx+c<0(a>0)的形式;
②求出相应的一元二次方程的根或利用二次函数的图象与根的判别式确定一元二次不等式的解集.(2)含参数的一元二次不等式
解题时应先看二次项系数的正负,其次考虑判别式,最后分析两根的大小,此种情况讨论是必不可少的.【巩固训练】(2016·武汉高二检测)已知a<0,解关于x的不等式ax2-(a-2)x-2<0.【解析】原不等式?
①当a<-2时,x>1或x<- ,
②当a=-2时,x≠1,
③当-2- 或x<1.综上所述:
当a<-2时,原不等式的解集为
当a=-2时,原不等式的解集为{x|x≠1},
当-2【典例3】(1)(2015·湖北高考)设变量x,y满足约束条
件 则3x+y的最大值为______.(2)某工厂有A,B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排方法所获利润最大?【解析】(1)由约束条件得其表示的平面区域如图所
示,由图象可得:目标函数z=3x+y过点B时z取最大值,
由 得 B(3,1),即zmax=3×3+1=10.
答案:10(2)设甲、乙两种产品分别生产x,y件,工厂获得的利润
为z,由题意可得 目标函数为z=2x+3y,
作出线性约束条件表示的可行域
如图所示:把z=2x+3y变形为y=- x+ ,这时斜率为- ,在y轴上
截距为 的直线,当z变化时,可以得到一簇相互平行的
直线,当截距 最大时,z取得最大值,由图象可以看出,
y=- x+ 过直线x=4与直线x+2y-8=0的交点M(4,2)时,
截距 的值最大,最大值为 ,此时2x+3y=14,所以每天
生产甲产品4件,乙产品2件时,工厂可获得最大利润14
万元.【规律总结】解线性规划实际应用题的步骤
(1)设出所求的未知数,列出约束条件,建立目标函数.
(2)作出可行域.
(3)确定平移直线,寻找最优解.
(4)检验,考虑最优解是否符合实际意义.【巩固训练】(2016·吉林高二检测)已知实数x,y满足
平面区域D: 则x2+y2的最大值为 ( )
A. B.1 C. D.8【解析】选D.平面区域为一个三角形ABC及其内部,其中A(1,0),B(0,1),C(2,2),x2+y2表示可行域内一点P到原点距离的平方,所以最大值为OC2=8.类型四:基本不等式及应用
【典例4】如图所示,某公园要在一块矩形绿地的中央
修建两个相同的矩形池塘,每个池塘的面积为10000m2,
池塘前方要留4m宽的走道,其余各方留2m宽的走道,问:
每个池塘的长和宽分别为多少时绿
地总面积最小?【解析】设池塘的长为xm时绿地总面积为S,
则池塘的宽y= (x>0).
所以S=
当且仅当 =6x,即x=100 ,y=50 时,等号成
立.故每个池塘的长为100 m,宽为50 m时,绿地总面积
最小.【规律总结】利用基本不等式求最值的解题技巧及注意事项
(1)利用基本不等式求最值的解题技巧
①凑项;②凑系数;③分离;④换元;⑤在应用基本不等式时,若遇到等号取不到的情况,结合函数的单调性;
⑥整体代换;⑦取平方.(2)注意事项
①要注意适用条件和范围:“一正、二定、三相等”;
②若等号取不到时,要注意利用函数的单调性求最值.【巩固训练】若正数x,y满足2x+y-3=0,则 的最
小值为________.【解析】由题意:2x+y-3=0?
所以
当且仅当x=y=1时取得最小值.
答案:3
第三章类型一:不等关系与不等式的性质
【典例1】(1)下列结论正确的是 ( )
A.若ac>bc,则a>b
B.若a2>b2,则a>b
C.若a>b,c<0,则a+c
|b|,故B项是错的;对于C项,应该是不等式的两边同时加上一个数,不等号的方向不变,故C错;对于D项涉及不等式的乘方运算性质,只有D对.(2)因为
因为a>0,b>0,且a≠b,
所以(a-b)2>0,a+b>0,ab>0,
所以 即 >a+b.【规律总结】
1.比较大小的方法及步骤
(1)作差法,步骤如下:①作差;②变形;③判断差的符号;④结论.
(2)作商法,步骤如下:①作商;②变形;③判断商与1的关系;④结论.2.作差法及作商法的目的及适用类型
(1)目的:作差的目的是判断差的符号,而作商的目的是判断商与1的大小.两种方法的关键是变形,常用的变形技巧有因式分解、配方、有理化等.
(2)适用类型:当两个代数式的正负不确定且为多项式形式时,常用作差法比较大小,当两个代数式均为正且均为幂的乘积式时,常用作商法比较大小.【巩固训练】若x∈R,则 与 的大小关系为
________.【解析】
所以
答案: 类型二:不等式的解法
【典例2】(2016·遵义高二检测)若不等式(1-a)x2-4x+6>0的解集是{x|-3
(2)b为何值时,ax2+bx+3≥0的解集为R.【解析】(1)由题意知1-a<0,且-3和1是方程(1-a)x2-
4x+6=0的两根,故 即a=3,
原不等式?2x2-x-3>0?(x+1)(2x-3)>0
?x> 或x<-1.即原不等式的解集为
(2)因为3x2+bx+3≥0的解集为R,
所以Δ=b2-4×3×3≤0,故-6≤b≤6.【规律总结】一元二次不等式的解法
(1)一元二次不等式的解法
①将不等式化为ax2+bx+c>0(a>0)
或ax2+bx+c<0(a>0)的形式;
②求出相应的一元二次方程的根或利用二次函数的图象与根的判别式确定一元二次不等式的解集.(2)含参数的一元二次不等式
解题时应先看二次项系数的正负,其次考虑判别式,最后分析两根的大小,此种情况讨论是必不可少的.【巩固训练】(2016·武汉高二检测)已知a<0,解关于x的不等式ax2-(a-2)x-2<0.【解析】原不等式?
①当a<-2时,x>1或x<- ,
②当a=-2时,x≠1,
③当-2
当a<-2时,原不等式的解集为
当a=-2时,原不等式的解集为{x|x≠1},
当-2
件 则3x+y的最大值为______.(2)某工厂有A,B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排方法所获利润最大?【解析】(1)由约束条件得其表示的平面区域如图所
示,由图象可得:目标函数z=3x+y过点B时z取最大值,
由 得 B(3,1),即zmax=3×3+1=10.
答案:10(2)设甲、乙两种产品分别生产x,y件,工厂获得的利润
为z,由题意可得 目标函数为z=2x+3y,
作出线性约束条件表示的可行域
如图所示:把z=2x+3y变形为y=- x+ ,这时斜率为- ,在y轴上
截距为 的直线,当z变化时,可以得到一簇相互平行的
直线,当截距 最大时,z取得最大值,由图象可以看出,
y=- x+ 过直线x=4与直线x+2y-8=0的交点M(4,2)时,
截距 的值最大,最大值为 ,此时2x+3y=14,所以每天
生产甲产品4件,乙产品2件时,工厂可获得最大利润14
万元.【规律总结】解线性规划实际应用题的步骤
(1)设出所求的未知数,列出约束条件,建立目标函数.
(2)作出可行域.
(3)确定平移直线,寻找最优解.
(4)检验,考虑最优解是否符合实际意义.【巩固训练】(2016·吉林高二检测)已知实数x,y满足
平面区域D: 则x2+y2的最大值为 ( )
A. B.1 C. D.8【解析】选D.平面区域为一个三角形ABC及其内部,其中A(1,0),B(0,1),C(2,2),x2+y2表示可行域内一点P到原点距离的平方,所以最大值为OC2=8.类型四:基本不等式及应用
【典例4】如图所示,某公园要在一块矩形绿地的中央
修建两个相同的矩形池塘,每个池塘的面积为10000m2,
池塘前方要留4m宽的走道,其余各方留2m宽的走道,问:
每个池塘的长和宽分别为多少时绿
地总面积最小?【解析】设池塘的长为xm时绿地总面积为S,
则池塘的宽y= (x>0).
所以S=
当且仅当 =6x,即x=100 ,y=50 时,等号成
立.故每个池塘的长为100 m,宽为50 m时,绿地总面积
最小.【规律总结】利用基本不等式求最值的解题技巧及注意事项
(1)利用基本不等式求最值的解题技巧
①凑项;②凑系数;③分离;④换元;⑤在应用基本不等式时,若遇到等号取不到的情况,结合函数的单调性;
⑥整体代换;⑦取平方.(2)注意事项
①要注意适用条件和范围:“一正、二定、三相等”;
②若等号取不到时,要注意利用函数的单调性求最值.【巩固训练】若正数x,y满足2x+y-3=0,则 的最
小值为________.【解析】由题意:2x+y-3=0?
所以
当且仅当x=y=1时取得最小值.
答案:3
