人教A版高中数学必修二3.2.3直线的一般式方程课件(共20张PPT)
文档属性
| 名称 | 人教A版高中数学必修二3.2.3直线的一般式方程课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 302.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-07 00:00:00 | ||
图片预览

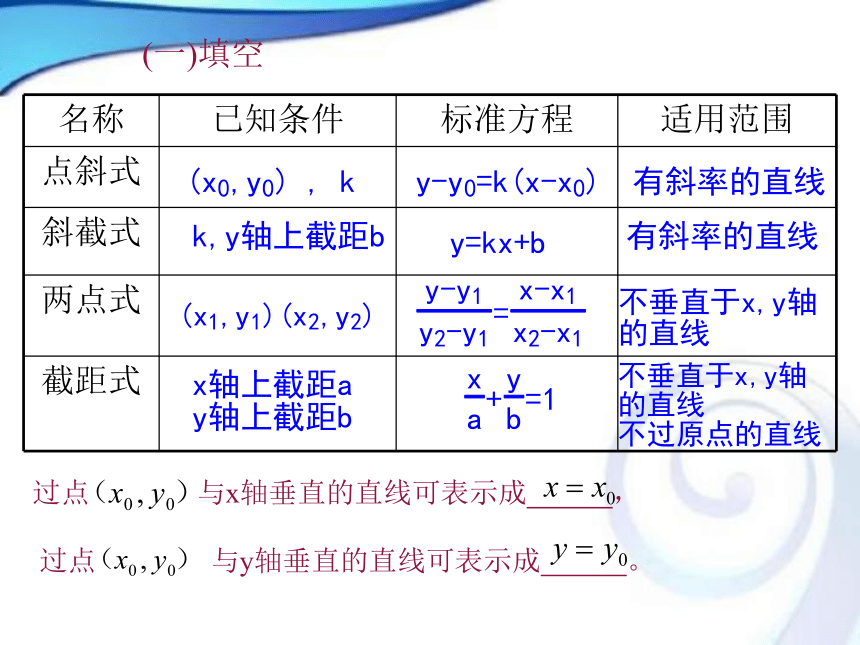







文档简介
课件20张PPT。3.2.3 直线的一般式方程 (一)填空(二)填空
1.过点(2,1),斜率为2的直线的方程是____________
2.过点(2,1),斜率为0的直线方程是___________
3.过点(2,1),斜率不存在的直线的方程是_________ 思考1:以上三个方程是否都是二元一次方程? 所有的直线方程是否都是二元一次方程?1.明确直线方程一般式的形式特征.(重点)
2.会把直线方程的一般式化为斜截式,进而求斜率
和截距.(难点)
3.会把直线方程的点斜式、两点式化为一般式.
(难点)Ax+By+C=0(A,B不同时为0)我们把关于x,y的二元一次方程叫做直线的一般式方程,简称一般式.一般式适用于任意一条直线.探究1:直线的一般式方程特别:对于直线方程的一般式,一般作如下约定: x的系数为正,x,y的系数及常数项一般不出现分数,一般按含x项、y项、常数项的顺序排列. 直线的点斜式、斜截式、两点式、截距式方程都是关于x,y的方程,上述四种直线方程,能否写成如Ax+ By+C=0(A,B不同时为0)的统一形式?
点斜式:探究2:一般式方程与其他形式方程的转化斜截式:y=kx+b kx-y+b=0
两点式: (y1-y2)x+(x2-x1)y+ x1y2-x2y1=0
截距式: bx+ay-ab=0例1 已知直线经过点A(6,- 4),斜率为 ,求直线的点斜式和一般式方程.解:经过点A(6,-4),斜率为 的直线的点斜式
方程为化成一般式,得4x+3y-12=0.例2 把直线l的一般式方程x-2y+6=0化成斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.解:将原方程化成斜截式得因此,直线l的斜率 ,它在y轴上的截距是3,在直线l的方程x-2y+6=0中,令y=0,可得 x=-6,即直线l在x轴上的截距是-6.例3 已知直线l1:ax+(a+1)y-a=0和 l2:(a+2)x+2(a+1)y-4=0,若l1//l2,求a的值.1.若直线l在x轴上的截距为-4,倾斜角的正切值为1,
则直线l的点斜式方程是___________.
直线l的斜截式方程是___________.
直线l的一般式方程是___________.y-0=x+4y=x+4x-y+4=0解:(1)x+2y-4=0. 2.根据下列条件,写出直线的一般式方程:(2)y-2=0. (3)2x-y-3=0. (4)x+y-1=0.5-53.求下列直线的斜率以及在y轴上的截距,并画出图形.4.已知线段PQ两端点的坐标分别为P(-1,1)和
Q(2,2),若直线l:x+my+m=0与线段PQ有交点,
求实数m的取值范围.
解:如图所示,直线l:x+my+m=0过定点
A(0,-1),当m≠0时,解得 或 当m=0时,直线l的方程为x=0,与线段PQ有交点,所以,实数m的取值范围为1.直线方程的一般式Ax+By+C=0(A,B不同时为0)2.直线方程的一般式与特殊式的互化.3.两条直线平行与垂直的判定.
1.过点(2,1),斜率为2的直线的方程是____________
2.过点(2,1),斜率为0的直线方程是___________
3.过点(2,1),斜率不存在的直线的方程是_________ 思考1:以上三个方程是否都是二元一次方程? 所有的直线方程是否都是二元一次方程?1.明确直线方程一般式的形式特征.(重点)
2.会把直线方程的一般式化为斜截式,进而求斜率
和截距.(难点)
3.会把直线方程的点斜式、两点式化为一般式.
(难点)Ax+By+C=0(A,B不同时为0)我们把关于x,y的二元一次方程叫做直线的一般式方程,简称一般式.一般式适用于任意一条直线.探究1:直线的一般式方程特别:对于直线方程的一般式,一般作如下约定: x的系数为正,x,y的系数及常数项一般不出现分数,一般按含x项、y项、常数项的顺序排列. 直线的点斜式、斜截式、两点式、截距式方程都是关于x,y的方程,上述四种直线方程,能否写成如Ax+ By+C=0(A,B不同时为0)的统一形式?
点斜式:探究2:一般式方程与其他形式方程的转化斜截式:y=kx+b kx-y+b=0
两点式: (y1-y2)x+(x2-x1)y+ x1y2-x2y1=0
截距式: bx+ay-ab=0例1 已知直线经过点A(6,- 4),斜率为 ,求直线的点斜式和一般式方程.解:经过点A(6,-4),斜率为 的直线的点斜式
方程为化成一般式,得4x+3y-12=0.例2 把直线l的一般式方程x-2y+6=0化成斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.解:将原方程化成斜截式得因此,直线l的斜率 ,它在y轴上的截距是3,在直线l的方程x-2y+6=0中,令y=0,可得 x=-6,即直线l在x轴上的截距是-6.例3 已知直线l1:ax+(a+1)y-a=0和 l2:(a+2)x+2(a+1)y-4=0,若l1//l2,求a的值.1.若直线l在x轴上的截距为-4,倾斜角的正切值为1,
则直线l的点斜式方程是___________.
直线l的斜截式方程是___________.
直线l的一般式方程是___________.y-0=x+4y=x+4x-y+4=0解:(1)x+2y-4=0. 2.根据下列条件,写出直线的一般式方程:(2)y-2=0. (3)2x-y-3=0. (4)x+y-1=0.5-53.求下列直线的斜率以及在y轴上的截距,并画出图形.4.已知线段PQ两端点的坐标分别为P(-1,1)和
Q(2,2),若直线l:x+my+m=0与线段PQ有交点,
求实数m的取值范围.
解:如图所示,直线l:x+my+m=0过定点
A(0,-1),当m≠0时,解得 或 当m=0时,直线l的方程为x=0,与线段PQ有交点,所以,实数m的取值范围为1.直线方程的一般式Ax+By+C=0(A,B不同时为0)2.直线方程的一般式与特殊式的互化.3.两条直线平行与垂直的判定.
