人教A版高中数学必修五3.3.1二元一次不等式(组)与平面区域(1)课件(共31张PPT)
文档属性
| 名称 | 人教A版高中数学必修五3.3.1二元一次不等式(组)与平面区域(1)课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-06 08:17:54 | ||
图片预览










文档简介
课件31张PPT。3.3 二元一次不等式(组)与简单的线性规划问题
3.3.1 二元一次不等式(组)与平面区域
第1课时 二元一次不等式表示的平面区域1.一家银行的信贷部计划年初投入25 000 000元用于企业和个人贷款,希望这笔资金至少可带来30 000元的收益,其中企业贷款获益12%,个人贷款获益10%. 上述问题应该用什么不等式模型来刻画呢? 2.以二元一次方程Ax+By+C=0的解为坐标的点________,在直线上的所有点的坐标__________.在线外的点的坐标与方程有何关系呢?
3.点A(1,1),B(2,1),C(-1,0)与直线x-y=0位置关系是什么?
4.我们知道x+y-1=0表示直线,而x2+(y-1)2=3表示圆,试考虑一下,x+y-1>0表示何种图形?在直线上适合方程1.了解二元一次不等式的几何意义和什么是边界,会用二元一次不等式表示平面区域;(难点)
2.经历从实际情境中抽象出二元一次不等式的过程,提高数学建模的能力.(难点) 设用于企业贷款的资金为x元,用于个人贷款的资金为y元.由资金总数为25 000 000元,得到1.二元一次不等式:
含有两个未知数,并且未知数的次数是1的不等式.探究点1 二元一次不等式的有关概念由于预计企业贷款创收12%,个人贷款创收10%,共创收30 000元以上,所以即②最后考虑到用于企业贷款和个人贷款的资金数额都不能是负值,所以③2.二元一次不等式的解集: 满足二元一次不等式的x和y的取值构成有序数对(x,y),所有这样的有序数对(x,y)构成的集合称为二元一次不等式的解集. 有序数对可以看成直角坐标平面内点的坐标.于是,二元一次不等式的解集就可以看成直角坐标系内的点构成的集合. 例如二元一次不等式x-y<6的解集为:
提示:{(x,y)|x-y<6}.二元一次不等式的概念
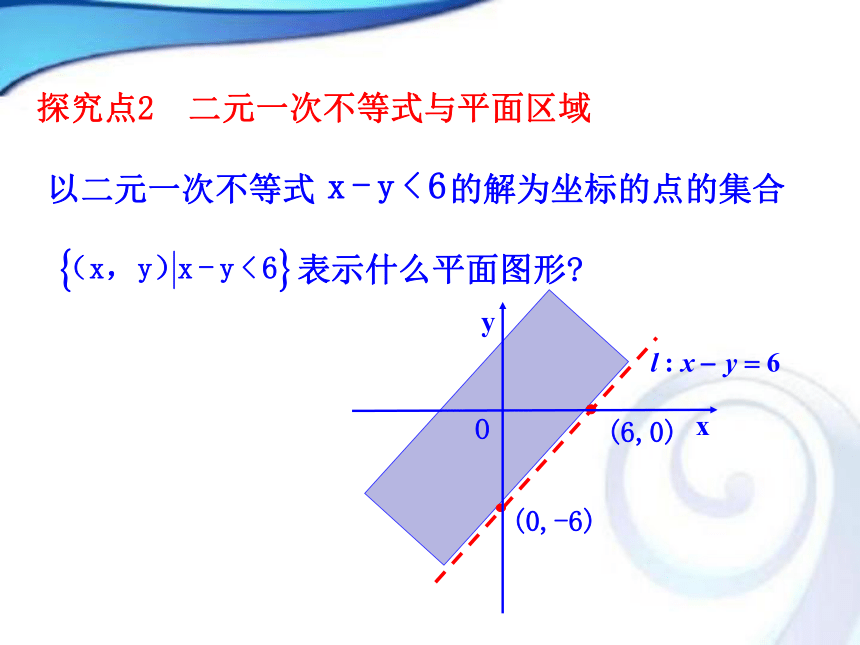
含有 未知数,并且未知数的次数是 的不等式叫做二元一次不等式.两个一次【即时练习】以二元一次不等式 的解为坐标的点的集合
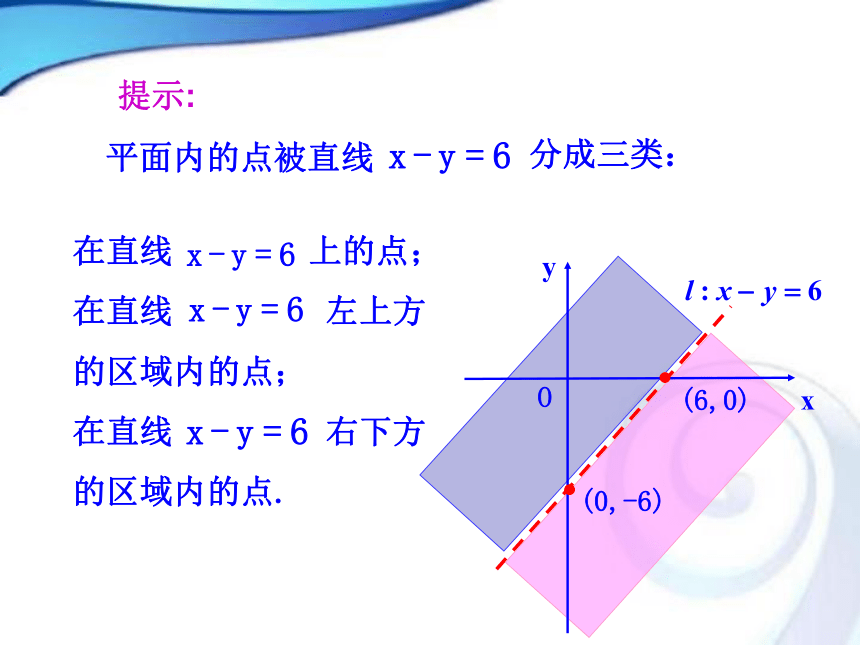
表示什么平面图形? 探究点2 二元一次不等式与平面区域在直线 上的点;
在直线 左上方
的区域内的点;
在直线 右下方
的区域内的点.平面内的点被直线分成三类:提示:横坐标点 的纵坐标点 的纵坐标-3-2-10123-9-8-7-6-5-4-3>-9>-8>-7>-6>-5>-4>-3 当点A与点P有相同的横坐标时,它们的纵坐标有什么关系?据此说说直线l左上方点的坐标与不等式x-y<6有什么关系?直线l右下方点的坐标呢? 我们发现,在平面直角坐标系中,以二元一次不等式 x-y<6的解为坐标的点都在直线x-y=6的左上方;反之,直线x-y=6左上方点的坐标都满足不等式x-y<6.直线x-y=6右下方点的坐标满足不等式x-y>6.提示:点A的纵坐标大于点P的纵坐标. 因此,在平面直角坐标系中,不等式x-y<6表示直线x-y=6左上方的平面区域.xO yxO y不等式x-y>6表示直线x-y=6右下方的平面区域.直线x-y=6叫做这两个区域的边界.
这里,把直线x-y=6画成虚线,以表示区域不包括边界.【规律总结】(3)区域确定:不等式2x+y-5>0表示的平面区域在
直线2x+y-5=0的( )
A.右上方 B.右下方
C.左上方 D.左下方A【即时练习】【解析】先作出边界2x+y-5=0,因为这条直线上的点都不满足2x+y-5>0,所以画成虚线.取原点(0,0),代入2x+y-5.因为2×0+0-5=-5<0,所以原点 (0,0)不在2x+y-5>0表示的平面区域内,不等式2x+y-5>0表示的区域如图所示(阴影部分),即在直线2x+y-5=0的右上方.故选A.例 画出不等式 表示的平面区域.不等式 表示的区域如图所示.表示的平面区域内,取原点(0,0),因为
所以原点(0,0)在注意虚实线画出下列不等式表示的平面区域:
(1)x+2y-4>0;(2)y≥x+3.【解题关键】
画二元一次不等式表示的平面区域的一般步骤为:第一步:“直线定界”,即画出边界直线Ax+By+C=0,要注意是虚线还是实线;
第二步:“特殊点定域”,取某个特殊点(x0,y0)作为测试点,由Ax0+By0+C的符号就可以确定出所给不等式表示的平面区域.【变式练习】【解析】(1)先作出边界x+2y-4=0,因为这条直线上的点都不满足x+2y-4>0,所以画成虚线.
取原点(0,0)代入x+2y-4.因为0+2×0-4=-4<0,所以原点(0,0),不在x+2y-4>0表示的平面区域内,不等式x+2y-4>0表示的平面区域如图(1)所示(阴影部分).(2)将y≥x+3变形为x-y+3≤0,先作出边界x-y+3=0,因为这条直线上的点都满足x-y+3≤0,所以画成实线.
取原点(0,0),代入x-y+3.因为0-0+3=3>0,所以原点(0,0)不在x-y+3≤0表示的平面区域内,不等式x-y+3≤0表示的平面区域如图(2)所示(阴影部分).【规律总结】
(1)y=kx+b表示的直线将平面分成两部分,即y>kx+b表示直线上方的平面区域,y<kx+b表示直线下方的平面区域,而直线y=kx+b是这两个区域的分界线.
(2)一般地,若Ax+By+C>0,则当B>0时,表示直线Ax+By+C=0上方的平面区域;当B<0时,表示直线Ax+By+C=0下方的平面区域.若Ax+By+C<0,与上述情况相反.
画出下面二元一次不等式表示的平面区域:
(1)2x-y-6≥0;(2)y>2x.
【解析】(1)如图,先画出直线2x-y-6=0,
取原点O(0,0)代入2x-y-6中,
∵2×0-0-6=-6<0,
∴与点O在直线2x-y-6=0同一侧的所有点(x,y)都满足2x-y-6<0,
故直线2x-y-6=0右下方的区域就是2x-y-6>0,
因此2x-y-6≥0表示直线下方的区域(包含边界).【互动探究】(2)画出直线y-2x=0,取点(1,0)代入y-2x=0
∵F(1,0)=0-2×1=-2<0,
∴y-2x>0(即y>2x)表示的区域为不含(1,0)的一侧,因此所求为如图所示的区域,不包括边界.1.不等式3x+2y–6≤0表示的平面区域是( )D 【解析】分别将P1、P2、P3点坐标代入3x+2y-1,比较发现只有3×0+2×0-1=-1<0,故P1点不在此平面区域内,P2、P3均在此平面区域内.
C3、画出不等式4x―3y≤12表示的平面区域.【解析】4.已知点(a,2a-1),既在直线y=3x-6的左上方,又在y轴的右侧,则a的取值范围为______________.
【解析】∵(a,2a-1)在y=3x-6的上方,
∴3a-6-(2a-1)<0,即a<5,又(a,2a-1)在y轴右侧,∴a>0,故0直线某一侧所有点组成的平面区域. 2. 判定方法:
直线定界,特殊点定域.(注意区分虚实线)
3.3.1 二元一次不等式(组)与平面区域
第1课时 二元一次不等式表示的平面区域1.一家银行的信贷部计划年初投入25 000 000元用于企业和个人贷款,希望这笔资金至少可带来30 000元的收益,其中企业贷款获益12%,个人贷款获益10%. 上述问题应该用什么不等式模型来刻画呢? 2.以二元一次方程Ax+By+C=0的解为坐标的点________,在直线上的所有点的坐标__________.在线外的点的坐标与方程有何关系呢?
3.点A(1,1),B(2,1),C(-1,0)与直线x-y=0位置关系是什么?
4.我们知道x+y-1=0表示直线,而x2+(y-1)2=3表示圆,试考虑一下,x+y-1>0表示何种图形?在直线上适合方程1.了解二元一次不等式的几何意义和什么是边界,会用二元一次不等式表示平面区域;(难点)
2.经历从实际情境中抽象出二元一次不等式的过程,提高数学建模的能力.(难点) 设用于企业贷款的资金为x元,用于个人贷款的资金为y元.由资金总数为25 000 000元,得到1.二元一次不等式:
含有两个未知数,并且未知数的次数是1的不等式.探究点1 二元一次不等式的有关概念由于预计企业贷款创收12%,个人贷款创收10%,共创收30 000元以上,所以即②最后考虑到用于企业贷款和个人贷款的资金数额都不能是负值,所以③2.二元一次不等式的解集: 满足二元一次不等式的x和y的取值构成有序数对(x,y),所有这样的有序数对(x,y)构成的集合称为二元一次不等式的解集. 有序数对可以看成直角坐标平面内点的坐标.于是,二元一次不等式的解集就可以看成直角坐标系内的点构成的集合. 例如二元一次不等式x-y<6的解集为:
提示:{(x,y)|x-y<6}.二元一次不等式的概念
含有 未知数,并且未知数的次数是 的不等式叫做二元一次不等式.两个一次【即时练习】以二元一次不等式 的解为坐标的点的集合
表示什么平面图形? 探究点2 二元一次不等式与平面区域在直线 上的点;
在直线 左上方
的区域内的点;
在直线 右下方
的区域内的点.平面内的点被直线分成三类:提示:横坐标点 的纵坐标点 的纵坐标-3-2-10123-9-8-7-6-5-4-3>-9>-8>-7>-6>-5>-4>-3 当点A与点P有相同的横坐标时,它们的纵坐标有什么关系?据此说说直线l左上方点的坐标与不等式x-y<6有什么关系?直线l右下方点的坐标呢? 我们发现,在平面直角坐标系中,以二元一次不等式 x-y<6的解为坐标的点都在直线x-y=6的左上方;反之,直线x-y=6左上方点的坐标都满足不等式x-y<6.直线x-y=6右下方点的坐标满足不等式x-y>6.提示:点A的纵坐标大于点P的纵坐标. 因此,在平面直角坐标系中,不等式x-y<6表示直线x-y=6左上方的平面区域.xO yxO y不等式x-y>6表示直线x-y=6右下方的平面区域.直线x-y=6叫做这两个区域的边界.
这里,把直线x-y=6画成虚线,以表示区域不包括边界.【规律总结】(3)区域确定:不等式2x+y-5>0表示的平面区域在
直线2x+y-5=0的( )
A.右上方 B.右下方
C.左上方 D.左下方A【即时练习】【解析】先作出边界2x+y-5=0,因为这条直线上的点都不满足2x+y-5>0,所以画成虚线.取原点(0,0),代入2x+y-5.因为2×0+0-5=-5<0,所以原点 (0,0)不在2x+y-5>0表示的平面区域内,不等式2x+y-5>0表示的区域如图所示(阴影部分),即在直线2x+y-5=0的右上方.故选A.例 画出不等式 表示的平面区域.不等式 表示的区域如图所示.表示的平面区域内,取原点(0,0),因为
所以原点(0,0)在注意虚实线画出下列不等式表示的平面区域:
(1)x+2y-4>0;(2)y≥x+3.【解题关键】
画二元一次不等式表示的平面区域的一般步骤为:第一步:“直线定界”,即画出边界直线Ax+By+C=0,要注意是虚线还是实线;
第二步:“特殊点定域”,取某个特殊点(x0,y0)作为测试点,由Ax0+By0+C的符号就可以确定出所给不等式表示的平面区域.【变式练习】【解析】(1)先作出边界x+2y-4=0,因为这条直线上的点都不满足x+2y-4>0,所以画成虚线.
取原点(0,0)代入x+2y-4.因为0+2×0-4=-4<0,所以原点(0,0),不在x+2y-4>0表示的平面区域内,不等式x+2y-4>0表示的平面区域如图(1)所示(阴影部分).(2)将y≥x+3变形为x-y+3≤0,先作出边界x-y+3=0,因为这条直线上的点都满足x-y+3≤0,所以画成实线.
取原点(0,0),代入x-y+3.因为0-0+3=3>0,所以原点(0,0)不在x-y+3≤0表示的平面区域内,不等式x-y+3≤0表示的平面区域如图(2)所示(阴影部分).【规律总结】
(1)y=kx+b表示的直线将平面分成两部分,即y>kx+b表示直线上方的平面区域,y<kx+b表示直线下方的平面区域,而直线y=kx+b是这两个区域的分界线.
(2)一般地,若Ax+By+C>0,则当B>0时,表示直线Ax+By+C=0上方的平面区域;当B<0时,表示直线Ax+By+C=0下方的平面区域.若Ax+By+C<0,与上述情况相反.
画出下面二元一次不等式表示的平面区域:
(1)2x-y-6≥0;(2)y>2x.
【解析】(1)如图,先画出直线2x-y-6=0,
取原点O(0,0)代入2x-y-6中,
∵2×0-0-6=-6<0,
∴与点O在直线2x-y-6=0同一侧的所有点(x,y)都满足2x-y-6<0,
故直线2x-y-6=0右下方的区域就是2x-y-6>0,
因此2x-y-6≥0表示直线下方的区域(包含边界).【互动探究】(2)画出直线y-2x=0,取点(1,0)代入y-2x=0
∵F(1,0)=0-2×1=-2<0,
∴y-2x>0(即y>2x)表示的区域为不含(1,0)的一侧,因此所求为如图所示的区域,不包括边界.1.不等式3x+2y–6≤0表示的平面区域是( )D 【解析】分别将P1、P2、P3点坐标代入3x+2y-1,比较发现只有3×0+2×0-1=-1<0,故P1点不在此平面区域内,P2、P3均在此平面区域内.
C3、画出不等式4x―3y≤12表示的平面区域.【解析】4.已知点(a,2a-1),既在直线y=3x-6的左上方,又在y轴的右侧,则a的取值范围为______________.
【解析】∵(a,2a-1)在y=3x-6的上方,
∴3a-6-(2a-1)<0,即a<5,又(a,2a-1)在y轴右侧,∴a>0,故0
直线定界,特殊点定域.(注意区分虚实线)
