人教A版高中数学必修五3.3.2简单的线性规划(2)课件(共47张PPT)
文档属性
| 名称 | 人教A版高中数学必修五3.3.2简单的线性规划(2)课件(共47张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-07 00:00:00 | ||
图片预览









文档简介
课件47张PPT。第2课时 简单线性规划的应用在实际问题中常遇到两类问题:
一是在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务; 二是给定一项任务,如何合理地安排和规划能以最少的人力、物力、资金等资源来完成它.下面我们来看看线性规划在实际中的一些应用. 1.体会线性规划的基本思想,并能借助几何直观解决一些简单的实际问题;(重点)
2.利用线性规划解决具有限制条件的不等式;
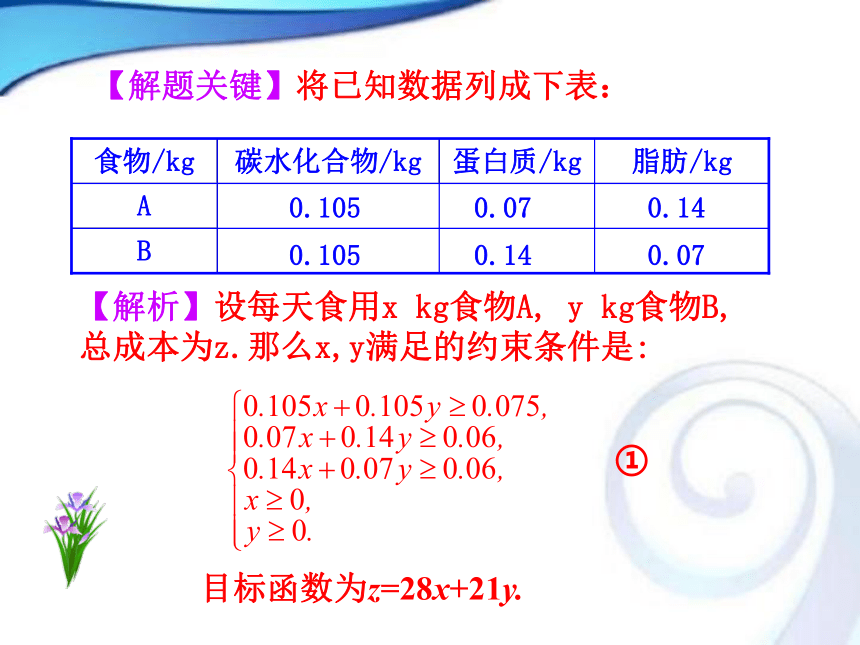
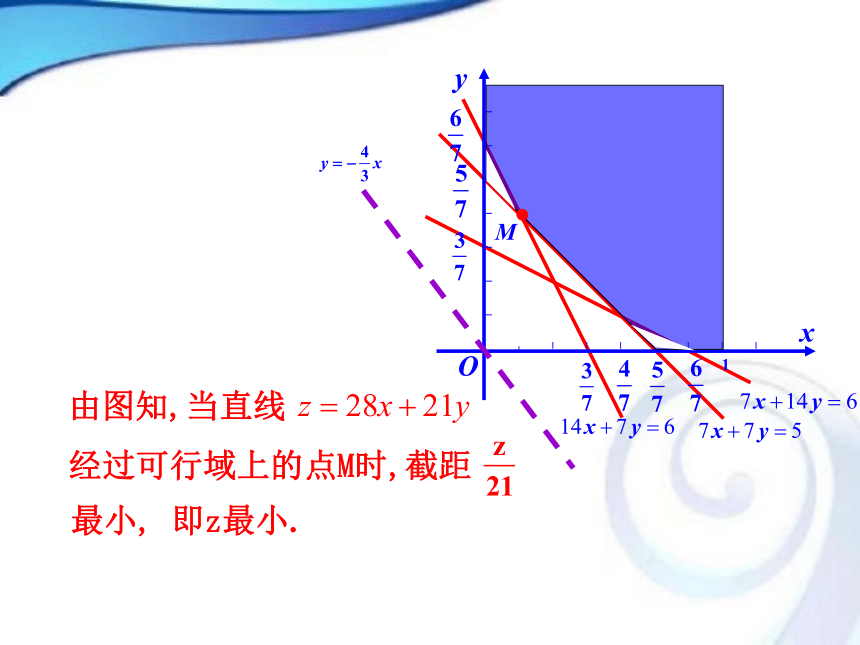
3.培养学生搜集、整理和分析信息的能力,提高学生数学建模和解决实际问题的能力.一、用量最省问题例1 营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪.1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg脂肪,花费28元;而1 kg食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?探究点1 简单线性规划问题及在实际问题中的应用【解题关键】将已知数据列成下表:【解析】设每天食用x kg食物A, y kg食物B, 总成本为z.那么x,y满足的约束条件是:①目标函数为z=28x+21y.作出二元一次不等式组②所表示的平面区域,即可行域. ②二元一次不等式组①等价于xOy由图知,当直线经过可行域上的点M时,截距最小, 即z最小.解方程组得M的坐标为所以zmin=28x+21y=16.答:每天食用食物A约143 g,食物B约571 g,能够满足日常饮食要求,又使花费最低,最低成本为16元. 解线性规划应用问题的一般步骤:
1.理清题意,列出表格;
2.设好变量,列出线性约束条件(不等式组)与目标函数;
3.准确作图;
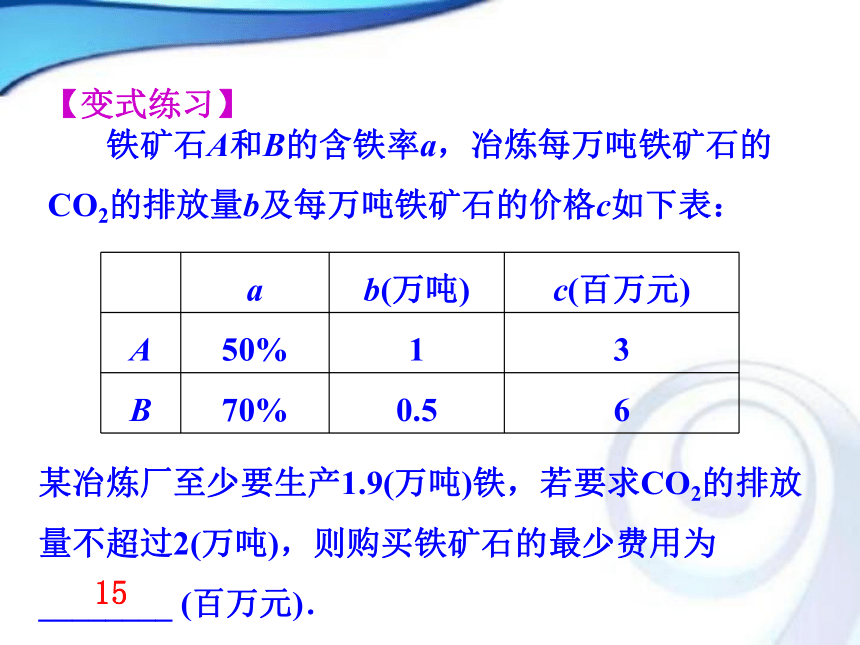
4.根据题设精确计算.【规律总结】 铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元).【变式练习】15目标函数为z=3x+6y,当目标函数经过(1,2)点时目标函数取最小值,最小值为:zmin=3×1+6×2=15.例2 要将两种大小不同的钢板截成A,B,C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示: 今需要A,B,C三种规格的成品分别15,18,27块,用数学关系式和图形表示上述要求.各截这两种钢板多少张可得所需A,B,C三种规格成品,且使所用钢板张数最少?规格类型钢板类型【解题关键】列表【解析】设需截第一种钢板x张,第二种钢板y张,共需截这两种钢板共z张,则线性目标函数2x+y=15x+3y=27x+2y=18xOy作出一组平行直线 z=x+y,当直线经过可行域上的点M时,z最小.作出可行域如图所示:由于 都不是整数,而此问题中的最优解
中, 必须都是整数,所以点 不是最优解.解方程组得使截距z最小的直线为 ,经过的整点是B(3,9)和C(4,8),它们是最优解.答:要截得所需三种规格的钢板,且使所截两种钢板张数最小的方法有两种,第一种截法是第一种钢板3张,第二种钢板9张;第二种截法是截第一种钢板4张,第二种钢板8张;两种截法都最少要两种钢板12张. 两类药片有效成分如下表所示,若要求至少提供12毫克阿司匹林,70毫克小苏打,28毫克可待因,问两类药片最小总数是多少?怎样搭配价格最低?【变式练习】由于A不是整点,因此不是z的最优解,结合图形可知,经过可行域内整点且与原点距离最近的直线是x+y=11,经过的整点是(1,10),(2,9),(3,8),
因此z的最小值为11.
药片最小总数为11片.
同理可得,当x=3,y=8时,k取最小值1.9,
因此当A类药品3片、B类药品8片时,药品价格最低.例3 一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4 t、硝酸盐18 t;生产1车皮乙种肥料需要的主要原料是磷酸盐1 t、硝酸盐15 t.现在库存磷酸盐10 t、硝酸盐66 t,在此基础上生产这两种混合肥料.列出满足生产条件的数学关系式,并画出相应的平面区域.若生产1车皮甲种肥料,产生的利润为10 000元;生产1车皮乙种肥料,产生的利润为5 000元.那么分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?二、效益最佳问题【解析】设生产x车皮甲种肥料、y车皮乙种肥料,能够产生利润z万元,则目标函数为418115甲种肥料乙种肥料磷酸盐(t)硝酸盐(t)总吨数车皮数利润(元)10 0005 000【解题关键】列表作出可行域,得到斜率为-2,在y轴上的截距为2z,随z变化的一族平行直线.答:生产甲、乙两种肥料各2车皮,能够产生最大利润,最大利润为3万元. 某工厂生产甲、乙两种产品.已知生产甲种产品
1 t需耗A种矿石10 t、B种矿石5 t、煤4 t;生产
乙种产品1 t需耗A种矿石4 t、B种矿石4 t、煤9 t.
每吨甲种产品的利润是600元,每吨乙种产品的利
润是1 000元. 工厂在生产这两种产品的计划中要
求消耗A种矿石不超过300 t、B种矿石不超过
200 t、煤不超过363 t.甲、乙两种产品应各生产
多少吨,能使利润总额达到最大?【变式练习】【解题关键】将已知数据列成下表:【解析】设生产甲、乙两种产品分别为x t、y t,利润总额为z元,则作出如图所示的可行域,解方程组:答:甲、乙两种产品应各生产12 t,35 t,能使利润总额达到最大,利润总额最大为42 200元.得点例4 若二次函数 的图象过原点,且
求 的范围.探究点2 利用简单线性规划求变量的范围作出如图所示的可行域, 将求变量范围的问题巧妙地转化为简单的线性规划问题进行求解,减少了失误.【规律总结】(2013·北京高考)设D为不等式组 表示的平面区域,区域D上的点与点(1,0)之间的距离的最小值为___________. 【变式练习】BD-5216000 1.设所求的未知数; 2.列出约束条件; 3.建立目标函数; 4.作出可行域; 5.运用图解法,求出最优解;
6.实际问题需要整数解时,适当调整,确定最优解.一、利用简单的线性规划解决实际问题的一般步骤:二、利用线性规划知识解决具有限制条件的函数不等式.
一是在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务; 二是给定一项任务,如何合理地安排和规划能以最少的人力、物力、资金等资源来完成它.下面我们来看看线性规划在实际中的一些应用. 1.体会线性规划的基本思想,并能借助几何直观解决一些简单的实际问题;(重点)
2.利用线性规划解决具有限制条件的不等式;
3.培养学生搜集、整理和分析信息的能力,提高学生数学建模和解决实际问题的能力.一、用量最省问题例1 营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪.1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg脂肪,花费28元;而1 kg食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元.为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?探究点1 简单线性规划问题及在实际问题中的应用【解题关键】将已知数据列成下表:【解析】设每天食用x kg食物A, y kg食物B, 总成本为z.那么x,y满足的约束条件是:①目标函数为z=28x+21y.作出二元一次不等式组②所表示的平面区域,即可行域. ②二元一次不等式组①等价于xOy由图知,当直线经过可行域上的点M时,截距最小, 即z最小.解方程组得M的坐标为所以zmin=28x+21y=16.答:每天食用食物A约143 g,食物B约571 g,能够满足日常饮食要求,又使花费最低,最低成本为16元. 解线性规划应用问题的一般步骤:
1.理清题意,列出表格;
2.设好变量,列出线性约束条件(不等式组)与目标函数;
3.准确作图;
4.根据题设精确计算.【规律总结】 铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元).【变式练习】15目标函数为z=3x+6y,当目标函数经过(1,2)点时目标函数取最小值,最小值为:zmin=3×1+6×2=15.例2 要将两种大小不同的钢板截成A,B,C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示: 今需要A,B,C三种规格的成品分别15,18,27块,用数学关系式和图形表示上述要求.各截这两种钢板多少张可得所需A,B,C三种规格成品,且使所用钢板张数最少?规格类型钢板类型【解题关键】列表【解析】设需截第一种钢板x张,第二种钢板y张,共需截这两种钢板共z张,则线性目标函数2x+y=15x+3y=27x+2y=18xOy作出一组平行直线 z=x+y,当直线经过可行域上的点M时,z最小.作出可行域如图所示:由于 都不是整数,而此问题中的最优解
中, 必须都是整数,所以点 不是最优解.解方程组得使截距z最小的直线为 ,经过的整点是B(3,9)和C(4,8),它们是最优解.答:要截得所需三种规格的钢板,且使所截两种钢板张数最小的方法有两种,第一种截法是第一种钢板3张,第二种钢板9张;第二种截法是截第一种钢板4张,第二种钢板8张;两种截法都最少要两种钢板12张. 两类药片有效成分如下表所示,若要求至少提供12毫克阿司匹林,70毫克小苏打,28毫克可待因,问两类药片最小总数是多少?怎样搭配价格最低?【变式练习】由于A不是整点,因此不是z的最优解,结合图形可知,经过可行域内整点且与原点距离最近的直线是x+y=11,经过的整点是(1,10),(2,9),(3,8),
因此z的最小值为11.
药片最小总数为11片.
同理可得,当x=3,y=8时,k取最小值1.9,
因此当A类药品3片、B类药品8片时,药品价格最低.例3 一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4 t、硝酸盐18 t;生产1车皮乙种肥料需要的主要原料是磷酸盐1 t、硝酸盐15 t.现在库存磷酸盐10 t、硝酸盐66 t,在此基础上生产这两种混合肥料.列出满足生产条件的数学关系式,并画出相应的平面区域.若生产1车皮甲种肥料,产生的利润为10 000元;生产1车皮乙种肥料,产生的利润为5 000元.那么分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?二、效益最佳问题【解析】设生产x车皮甲种肥料、y车皮乙种肥料,能够产生利润z万元,则目标函数为418115甲种肥料乙种肥料磷酸盐(t)硝酸盐(t)总吨数车皮数利润(元)10 0005 000【解题关键】列表作出可行域,得到斜率为-2,在y轴上的截距为2z,随z变化的一族平行直线.答:生产甲、乙两种肥料各2车皮,能够产生最大利润,最大利润为3万元. 某工厂生产甲、乙两种产品.已知生产甲种产品
1 t需耗A种矿石10 t、B种矿石5 t、煤4 t;生产
乙种产品1 t需耗A种矿石4 t、B种矿石4 t、煤9 t.
每吨甲种产品的利润是600元,每吨乙种产品的利
润是1 000元. 工厂在生产这两种产品的计划中要
求消耗A种矿石不超过300 t、B种矿石不超过
200 t、煤不超过363 t.甲、乙两种产品应各生产
多少吨,能使利润总额达到最大?【变式练习】【解题关键】将已知数据列成下表:【解析】设生产甲、乙两种产品分别为x t、y t,利润总额为z元,则作出如图所示的可行域,解方程组:答:甲、乙两种产品应各生产12 t,35 t,能使利润总额达到最大,利润总额最大为42 200元.得点例4 若二次函数 的图象过原点,且
求 的范围.探究点2 利用简单线性规划求变量的范围作出如图所示的可行域, 将求变量范围的问题巧妙地转化为简单的线性规划问题进行求解,减少了失误.【规律总结】(2013·北京高考)设D为不等式组 表示的平面区域,区域D上的点与点(1,0)之间的距离的最小值为___________. 【变式练习】BD-5216000 1.设所求的未知数; 2.列出约束条件; 3.建立目标函数; 4.作出可行域; 5.运用图解法,求出最优解;
6.实际问题需要整数解时,适当调整,确定最优解.一、利用简单的线性规划解决实际问题的一般步骤:二、利用线性规划知识解决具有限制条件的函数不等式.
