人教A版高中数学必修五3.2一元二次不等式及其解法(1)课件(共29张PPT)
文档属性
| 名称 | 人教A版高中数学必修五3.2一元二次不等式及其解法(1)课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-07 10:15:55 | ||
图片预览








文档简介
课件29张PPT。3.2 一元二次不等式及其解法
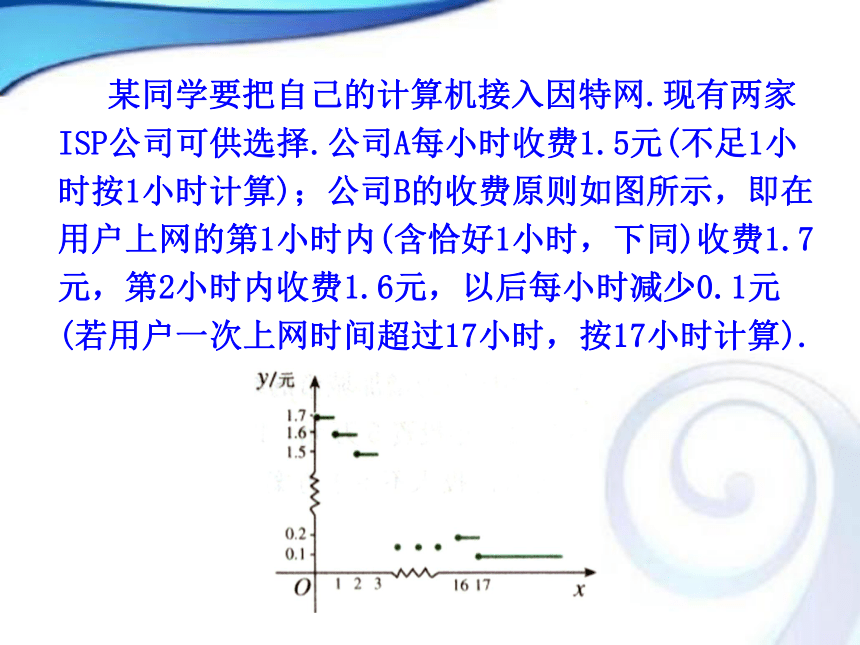
第1课时 一元二次不等式及其解法 上网获取信息已经成为人们日常生活的重要组成部分,因特网服务公司(ISP)的任务就是负责将用户的计算机接入因特网,同时收取一定的费用. 某同学要把自己的计算机接入因特网.现有两家ISP公司可供选择.公司A每小时收费1.5元(不足1小时按1小时计算);公司B的收费原则如图所示,即在用户上网的第1小时内(含恰好1小时,下同)收费1.7元,第2小时内收费1.6元,以后每小时减少0.1元(若用户一次上网时间超过17小时,按17小时计算).一般来说,一次上网时间不会超过17个小时,所以,不妨假设一次上网时间总小于17小时.那么,一次上网在多长时间以内能够保证选择公司A的上网费用小于或等于选择公司B所需费用? 这是一个关于x的一元二次不等式,只要求得满足不等式①的解集,就得到了问题的答案.如果能够保证选择公司A比选择公司B所需费用少或
相等,则1. 正确理解一元二次不等式的概念,掌握一元二次不等式的解法; (重点)
2. 理解一元二次不等式、二次函数及一元二次方程的关系,能借助二次函数的图象及一元二次方程解一元二次不等式. (难点)探究点1 一元二次不等式的概念(1)只含有一个未知数x;
(2)未知数的最高次数为2.不等式 有两个特点:我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.一元二次不等式的定义:一元二次不等式的一般表达式为ax2+bx+c>0(a≠0)
或ax2+bx+c<0 (a≠0),其中a,b,c均为常数.下列不等式中一元二次不等式的个数为( )
①(m+1)x2-3x+1<0;② >2;
③-x2+5x+6≥0;④(x+a)(x+a+1)<0.
A.1 B.2
C.3 D.4
【解析】③④符合一元二次不等式的定义;对于①,当m+1=0时,不是一元二次不等式;而②是指数不等式.
B【即时练习】怎样求一元二次不等式x2-5x≤0的解集?画出二次函数 的图象.(1) 当 取 时,y=0.
当 时,y>0.
当 时,y<0.y0或5y=x2-5x探究点2 一元二次不等式的解法提示: (2)由图象可知:
不等式 的解集为 ;
不等式 的解集为 . 所以,当一次上网时间在5小时以内(含恰好5小时)时,选择公司A的费用小于或等于选择公司B的费用;超过5小时,选择公司B的费用少.不等式
的解集是什么?无实根的图象完成下表:xxxyyyOOO一元二次不等式ax2+bx+c>0(a>0)的求解过程——程序框图是是否否R解不等式:
x2+2x-15>0
【解析】x2+2x-15>0?(x+5)(x-3)>0
?x<-5或x>3,
∴不等式的解集是{x|x<-5或x>3}.【即时练习】 例1 求不等式 的解集.解不等式:【变式练习】例2 求不等式 的解集.而 的图象开口向上,【解析】不等式可化为所以方程 无实数根,所以原不等式的解集为【解题关键】二次项系数为负数时,先转化为正数再求解.求不等式 的解集.而 的图象开口向上,【解析】不等式可化为所以方程 有两个实数根所以原不等式的解集为转化为一般形式【变式练习】(2)求方程 的根,解一元二次不等式的一般步骤:(1)化成不等式的标准形式:并画出对应的二次函数
的图象;【规律总结】简记为:大于0取两边,小于0取中间.(3)由图象得出不等式的解集:【规律总结】B
2.不等式(x-2)(x+3)>0的解集是( )
A.(-3,2) B.(2,+∞)
C.(-∞,-3)∪(2,+∞)
D.(-∞,-2)∪(3,+∞)
【解析】不等式(x-2)(x+3)>0的解集是(-∞,
-3)∪(2,+∞).C(-4,1) 而 的图象开口向上,【解析】(1)不等式可化为方程 有两个实数根所以原不等式的解集为5.解下列不等式:(2)原不等式化为
所以不等式的解集是 所以方程 有两个实数根(3)原不等式可化为
所以原不等式的解集是 回顾本节课你有什么收获?1.一元二次不等式的定义;2.一元二次不等式的解法及步骤;3.一元二次不等式与一元二次方程、一元二次函数的联系.
第1课时 一元二次不等式及其解法 上网获取信息已经成为人们日常生活的重要组成部分,因特网服务公司(ISP)的任务就是负责将用户的计算机接入因特网,同时收取一定的费用. 某同学要把自己的计算机接入因特网.现有两家ISP公司可供选择.公司A每小时收费1.5元(不足1小时按1小时计算);公司B的收费原则如图所示,即在用户上网的第1小时内(含恰好1小时,下同)收费1.7元,第2小时内收费1.6元,以后每小时减少0.1元(若用户一次上网时间超过17小时,按17小时计算).一般来说,一次上网时间不会超过17个小时,所以,不妨假设一次上网时间总小于17小时.那么,一次上网在多长时间以内能够保证选择公司A的上网费用小于或等于选择公司B所需费用? 这是一个关于x的一元二次不等式,只要求得满足不等式①的解集,就得到了问题的答案.如果能够保证选择公司A比选择公司B所需费用少或
相等,则1. 正确理解一元二次不等式的概念,掌握一元二次不等式的解法; (重点)
2. 理解一元二次不等式、二次函数及一元二次方程的关系,能借助二次函数的图象及一元二次方程解一元二次不等式. (难点)探究点1 一元二次不等式的概念(1)只含有一个未知数x;
(2)未知数的最高次数为2.不等式 有两个特点:我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.一元二次不等式的定义:一元二次不等式的一般表达式为ax2+bx+c>0(a≠0)
或ax2+bx+c<0 (a≠0),其中a,b,c均为常数.下列不等式中一元二次不等式的个数为( )
①(m+1)x2-3x+1<0;② >2;
③-x2+5x+6≥0;④(x+a)(x+a+1)<0.
A.1 B.2
C.3 D.4
【解析】③④符合一元二次不等式的定义;对于①,当m+1=0时,不是一元二次不等式;而②是指数不等式.
B【即时练习】怎样求一元二次不等式x2-5x≤0的解集?画出二次函数 的图象.(1) 当 取 时,y=0.
当 时,y>0.
当 时,y<0.y0或5y=x2-5x探究点2 一元二次不等式的解法提示: (2)由图象可知:
不等式 的解集为 ;
不等式 的解集为 . 所以,当一次上网时间在5小时以内(含恰好5小时)时,选择公司A的费用小于或等于选择公司B的费用;超过5小时,选择公司B的费用少.不等式
的解集是什么?无实根的图象完成下表:xxxyyyOOO一元二次不等式ax2+bx+c>0(a>0)的求解过程——程序框图是是否否R解不等式:
x2+2x-15>0
【解析】x2+2x-15>0?(x+5)(x-3)>0
?x<-5或x>3,
∴不等式的解集是{x|x<-5或x>3}.【即时练习】 例1 求不等式 的解集.解不等式:【变式练习】例2 求不等式 的解集.而 的图象开口向上,【解析】不等式可化为所以方程 无实数根,所以原不等式的解集为【解题关键】二次项系数为负数时,先转化为正数再求解.求不等式 的解集.而 的图象开口向上,【解析】不等式可化为所以方程 有两个实数根所以原不等式的解集为转化为一般形式【变式练习】(2)求方程 的根,解一元二次不等式的一般步骤:(1)化成不等式的标准形式:并画出对应的二次函数
的图象;【规律总结】简记为:大于0取两边,小于0取中间.(3)由图象得出不等式的解集:【规律总结】B
2.不等式(x-2)(x+3)>0的解集是( )
A.(-3,2) B.(2,+∞)
C.(-∞,-3)∪(2,+∞)
D.(-∞,-2)∪(3,+∞)
【解析】不等式(x-2)(x+3)>0的解集是(-∞,
-3)∪(2,+∞).C(-4,1) 而 的图象开口向上,【解析】(1)不等式可化为方程 有两个实数根所以原不等式的解集为5.解下列不等式:(2)原不等式化为
所以不等式的解集是 所以方程 有两个实数根(3)原不等式可化为
所以原不等式的解集是 回顾本节课你有什么收获?1.一元二次不等式的定义;2.一元二次不等式的解法及步骤;3.一元二次不等式与一元二次方程、一元二次函数的联系.
