人教A版高中数学选修2-12.3.2双曲线的简单几何性质课件(共29张PPT)
文档属性
| 名称 | 人教A版高中数学选修2-12.3.2双曲线的简单几何性质课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 741.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-07 10:18:47 | ||
图片预览







文档简介
课件29张PPT。2.3.2 双曲线的简单几何性质
我们知道,电能是现代生活不可缺少的能源,
目前我国主要靠火力发电,而火力发电主要是在
火力发电厂中进行,火力发电厂简称“火电厂”,
其形状就像照片中“粗烟囱”.那么这些“粗烟囱”
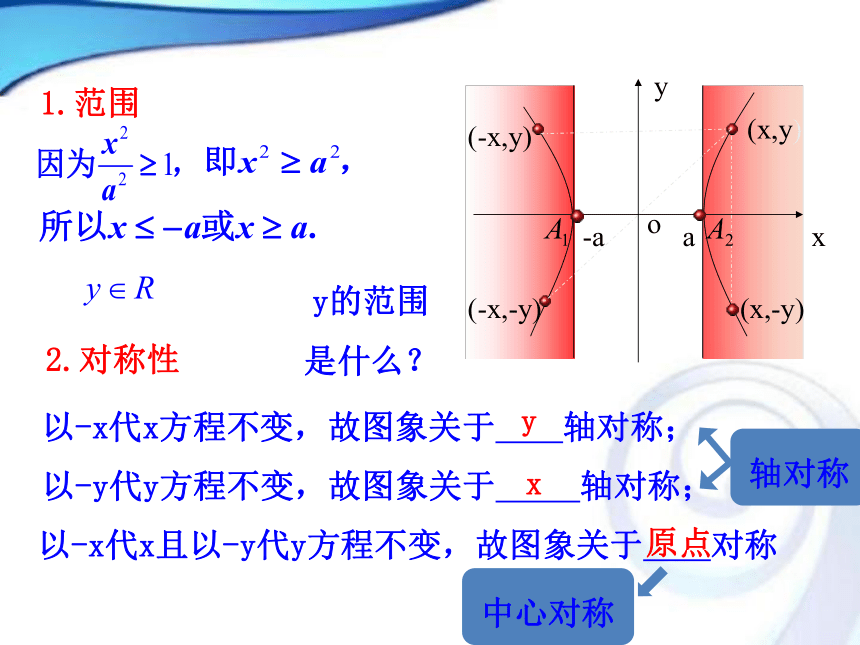
是怎样建成的呢?冷却通风塔如果你是设计师你将如何设计?探究点1 双曲线的简单几何性质回忆一下双曲线的标准方程: 如果我们也按照椭圆的几何性质的研究方法来研究双曲线,那么双曲线将会具有什么样的几何性质呢?1.范围(-x,-y)(-x,y)(x,-y)2.对称性 以-x代x方程不变,故图象关于 轴对称;以-y代y方程不变,故图象关于 轴对称;以-x代x且以-y代y方程不变,故图象关于 对称yx原点y的范围是什么?3.顶点(1)令y=0,得x=±a,则双曲线与x轴的两个交点为
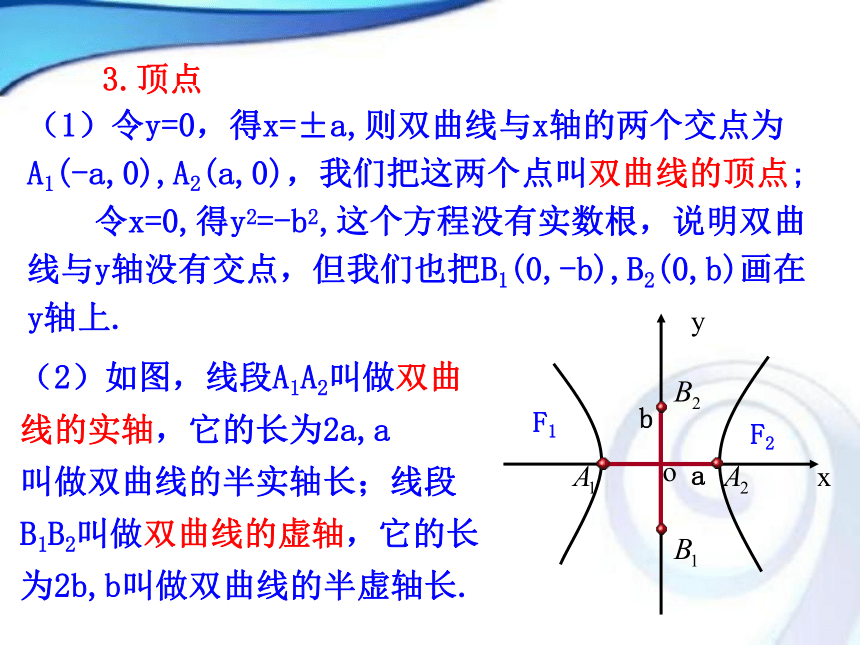
A1(-a,0),A2(a,0),我们把这两个点叫双曲线的顶点;
令x=0,得y2=-b2,这个方程没有实数根,说明双曲线与y轴没有交点,但我们也把B1(0,-b),B2(0,b)画在y轴上.(2)如图,线段A1A2叫做双曲线的实轴,它的长为2a,a
叫做双曲线的半实轴长;线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的半虚轴长.F2F1ab4.渐近线 下面我们证明双曲线上的点在沿曲线向远处运动时,与直线逐渐靠拢.方案2:考查同横坐标的两点间的距离 .yB2A1A2 B1 xOb aM NQ 由双曲线的对称性知,我们只需证明第一象限的部分即可.XMYOQN(x,y)(x,Y)注:渐近线是双曲线特有的几何性质,它决定着双曲线张口的开阔与否.实轴和虚轴等长的双曲线叫做等轴双曲线.5.离心率:思考:椭圆的离心率可以刻画椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征? 因此,e越大,渐近线斜率越大,倾斜角越大,张角越大,张口越开阔,e越小,渐近线斜率越小,倾斜角越小,张角越小,张口越扁狭. 所以双曲线的离心率是反应双曲线开口大小的几何量.关于坐标
轴和
原点
都对
称性质双曲线范围对称
性 顶点 渐近
线离心
率图象【总结提升】双曲线的简单几何性质.xyxy探究点2 由双曲线的性质求双曲线方程已知双曲线的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定双曲线方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.【总结提升】定位定量解:【例2】点M(x,y)与定点F(5,0)的距离和它到定
直线 的距离的比是常数 ,求点M的轨迹.xy..FOM.【变式练习】方程①两边平方化简整理得 ②方程②化为 ,∴点M的轨迹是实轴长为2a,虚轴长为2b的双曲线.双曲线中应注意的几个问题:
(1)双曲线是两支曲线,而椭圆是一条封闭的曲线;
(2)双曲线的两条渐近线是区别于其他圆锥曲线所特有的;
(3)双曲线只有两个顶点,离心率e>1;
(4)注意双曲线中a,b,c,e的等量关系与椭圆中a,b,c,e的不同.【总结提升】 回顾直线与椭圆的位置关系及判断方法,思考直线与双曲线有何位置关系,如何判断?种类: 相离; 相切; 相交(一个交点, 两个交点)探究点3 直线与双曲线的位置关系注意只有一个交点的相交与相切的区分1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与双曲线的方程,
消元得到一元二次方程(当二次项系数不为0时)
(1)△>0?直线与双曲线相交?有两个公共点;
(2)△=0?直线与双曲线相切?有且只有一个
公共点;
(3)△<0?直线与双曲线相离?无公共点.通法【总结提升】直线与双曲线的位置关系:解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0). 因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为【总结提升】这里我们也可以利用弦长公式求解.弦长公式:或算一算,看结果一样吗?【变式练习】解析:因为F1的坐标是(-3,0),所以关于坐标
轴和
原点
都对
称性质双曲线范围对称
性 顶点 渐近
线离心
率图象xyxy双曲线方程及性质的应用位置关系判断方法相交相切相离定位定量代数法距离公式弦长公式
我们知道,电能是现代生活不可缺少的能源,
目前我国主要靠火力发电,而火力发电主要是在
火力发电厂中进行,火力发电厂简称“火电厂”,
其形状就像照片中“粗烟囱”.那么这些“粗烟囱”
是怎样建成的呢?冷却通风塔如果你是设计师你将如何设计?探究点1 双曲线的简单几何性质回忆一下双曲线的标准方程: 如果我们也按照椭圆的几何性质的研究方法来研究双曲线,那么双曲线将会具有什么样的几何性质呢?1.范围(-x,-y)(-x,y)(x,-y)2.对称性 以-x代x方程不变,故图象关于 轴对称;以-y代y方程不变,故图象关于 轴对称;以-x代x且以-y代y方程不变,故图象关于 对称yx原点y的范围是什么?3.顶点(1)令y=0,得x=±a,则双曲线与x轴的两个交点为
A1(-a,0),A2(a,0),我们把这两个点叫双曲线的顶点;
令x=0,得y2=-b2,这个方程没有实数根,说明双曲线与y轴没有交点,但我们也把B1(0,-b),B2(0,b)画在y轴上.(2)如图,线段A1A2叫做双曲线的实轴,它的长为2a,a
叫做双曲线的半实轴长;线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的半虚轴长.F2F1ab4.渐近线 下面我们证明双曲线上的点在沿曲线向远处运动时,与直线逐渐靠拢.方案2:考查同横坐标的两点间的距离 .yB2A1A2 B1 xOb aM NQ 由双曲线的对称性知,我们只需证明第一象限的部分即可.XMYOQN(x,y)(x,Y)注:渐近线是双曲线特有的几何性质,它决定着双曲线张口的开阔与否.实轴和虚轴等长的双曲线叫做等轴双曲线.5.离心率:思考:椭圆的离心率可以刻画椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征? 因此,e越大,渐近线斜率越大,倾斜角越大,张角越大,张口越开阔,e越小,渐近线斜率越小,倾斜角越小,张角越小,张口越扁狭. 所以双曲线的离心率是反应双曲线开口大小的几何量.关于坐标
轴和
原点
都对
称性质双曲线范围对称
性 顶点 渐近
线离心
率图象【总结提升】双曲线的简单几何性质.xyxy探究点2 由双曲线的性质求双曲线方程已知双曲线的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定双曲线方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.【总结提升】定位定量解:【例2】点M(x,y)与定点F(5,0)的距离和它到定
直线 的距离的比是常数 ,求点M的轨迹.xy..FOM.【变式练习】方程①两边平方化简整理得 ②方程②化为 ,∴点M的轨迹是实轴长为2a,虚轴长为2b的双曲线.双曲线中应注意的几个问题:
(1)双曲线是两支曲线,而椭圆是一条封闭的曲线;
(2)双曲线的两条渐近线是区别于其他圆锥曲线所特有的;
(3)双曲线只有两个顶点,离心率e>1;
(4)注意双曲线中a,b,c,e的等量关系与椭圆中a,b,c,e的不同.【总结提升】 回顾直线与椭圆的位置关系及判断方法,思考直线与双曲线有何位置关系,如何判断?种类: 相离; 相切; 相交(一个交点, 两个交点)探究点3 直线与双曲线的位置关系注意只有一个交点的相交与相切的区分1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与双曲线的方程,
消元得到一元二次方程(当二次项系数不为0时)
(1)△>0?直线与双曲线相交?有两个公共点;
(2)△=0?直线与双曲线相切?有且只有一个
公共点;
(3)△<0?直线与双曲线相离?无公共点.通法【总结提升】直线与双曲线的位置关系:解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0). 因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为【总结提升】这里我们也可以利用弦长公式求解.弦长公式:或算一算,看结果一样吗?【变式练习】解析:因为F1的坐标是(-3,0),所以关于坐标
轴和
原点
都对
称性质双曲线范围对称
性 顶点 渐近
线离心
率图象xyxy双曲线方程及性质的应用位置关系判断方法相交相切相离定位定量代数法距离公式弦长公式
