人教A版高中数学选修2-12.4.1抛物线及其标准方程课件(共32张PPT)
文档属性
| 名称 | 人教A版高中数学选修2-12.4.1抛物线及其标准方程课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-06 08:23:05 | ||
图片预览





文档简介
课件32张PPT。
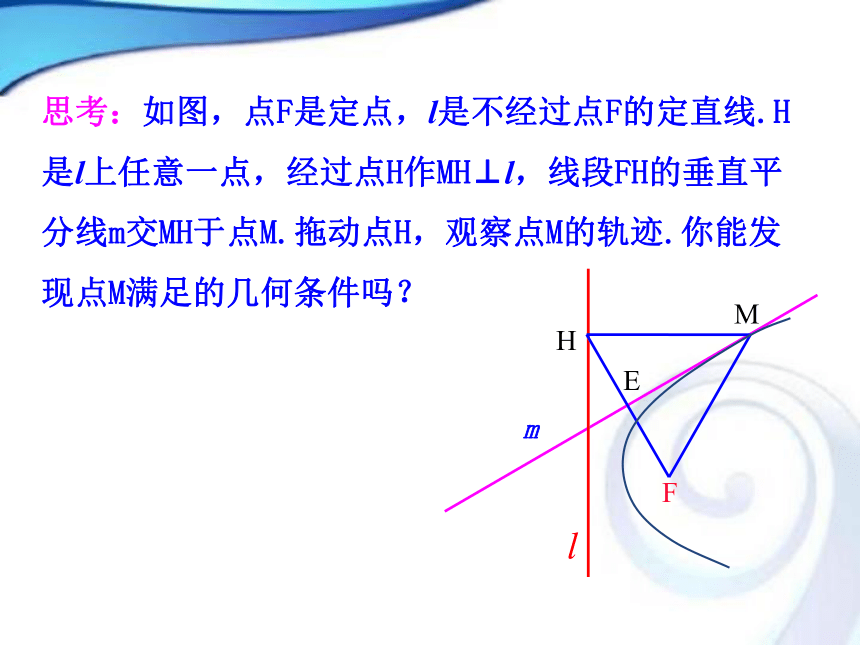
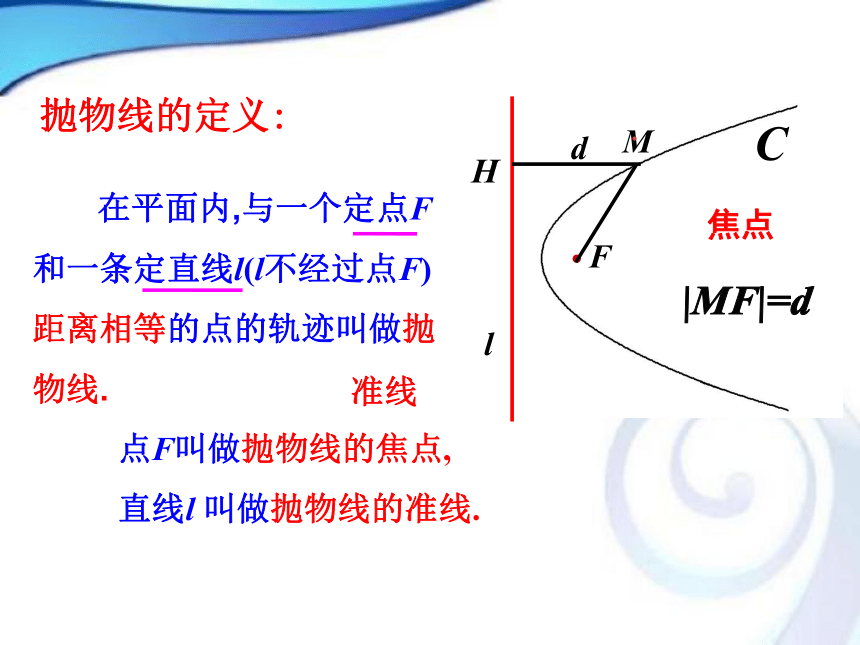
2.4.1 抛物线及其标准方程 生活中存在着各种形式的抛物线抛物线的生活实例 我们知道,二次函数y=ax2+bx+c(a≠0)的图象是一条抛物线,而且研究过它的顶点坐标、对称轴等问题.那么,抛物线是怎么定义的,方程是什么呢?探究点1 抛物线的定义MHFE思考:如图,点F是定点,l是不经过点F的定直线.H是l上任意一点,经过点H作MH⊥l,线段FH的垂直平分线m交MH于点M.拖动点H,观察点M的轨迹.你能发现点M满足的几何条件吗?m抛物线的定义: 在平面内,与一个定点F和一条定直线l(l不经过点F) 距离相等的点的轨迹叫做抛物线.|MF|=d焦点d准线点F叫做抛物线的焦点,
直线l 叫做抛物线的准线.明确了抛物线的定义,你能根据定义求出抛物线的
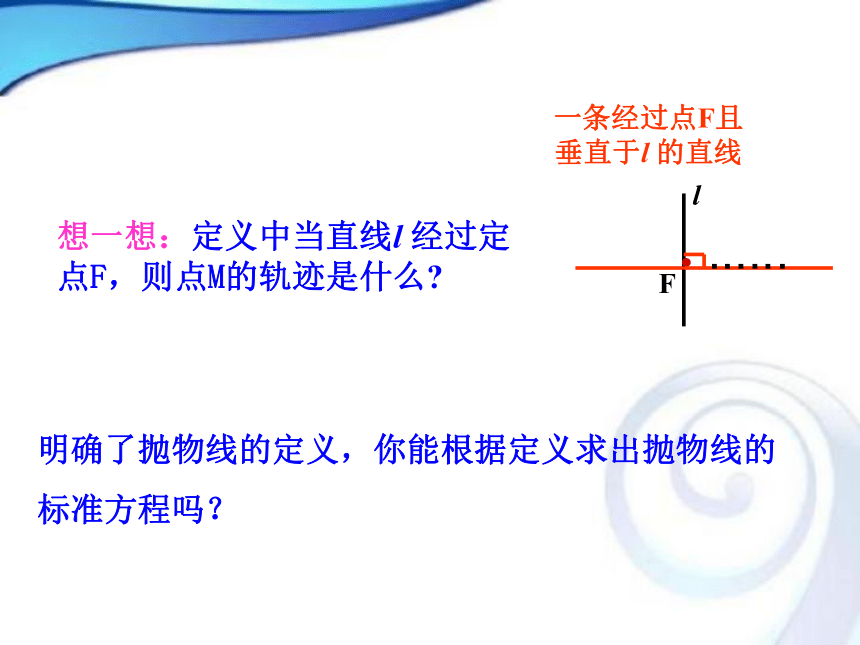
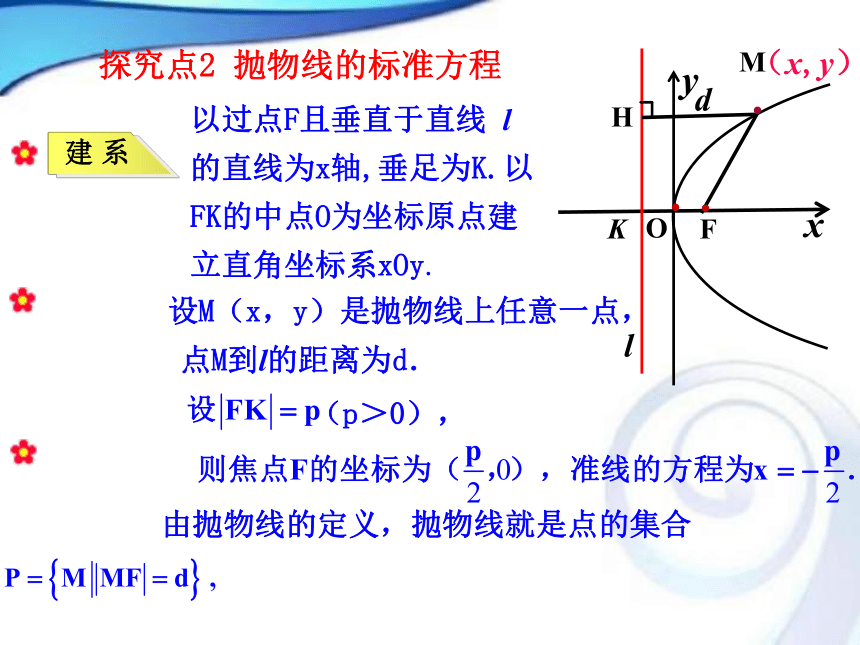
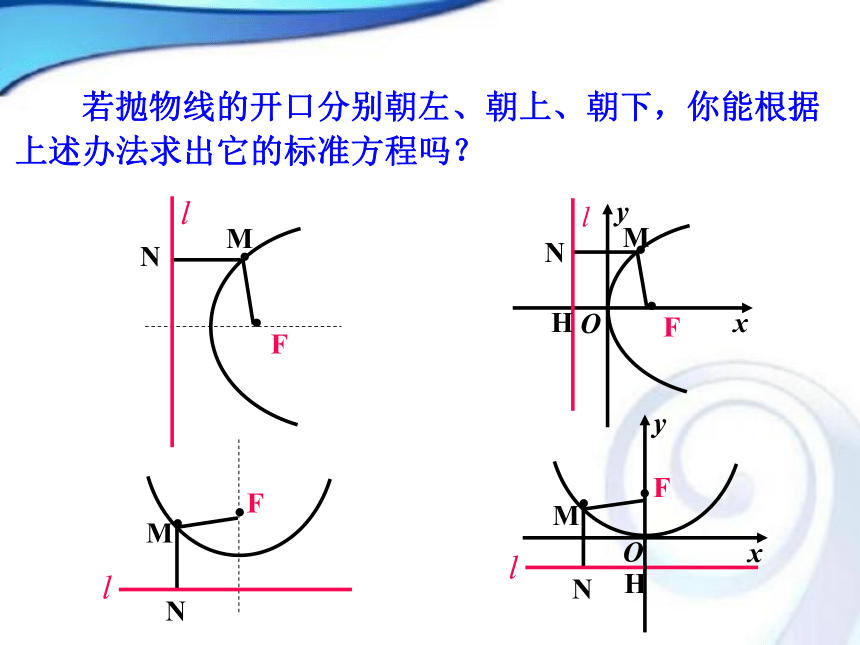
标准方程吗?一条经过点F且垂直于l 的直线想一想:定义中当直线l 经过定点F,则点M的轨迹是什么?······以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.KOFMl···(x,y)设M(x,y)是抛物线上任意一点,H点M到l的距离为d.d由抛物线的定义,抛物线就是点的集合探究点2 抛物线的标准方程两边平方,整理得KOFMl···(x, y)Hd其中p为正常数,它的几何意义是: 焦点到准线的距离.方程 y2 = 2px(p>0)表示焦点在x轴正半轴上的抛物线. 若抛物线的开口分别朝左、朝上、朝下,你能根据上述办法求出它的标准方程吗?O准线方程焦点坐标标准方程焦点位置 图
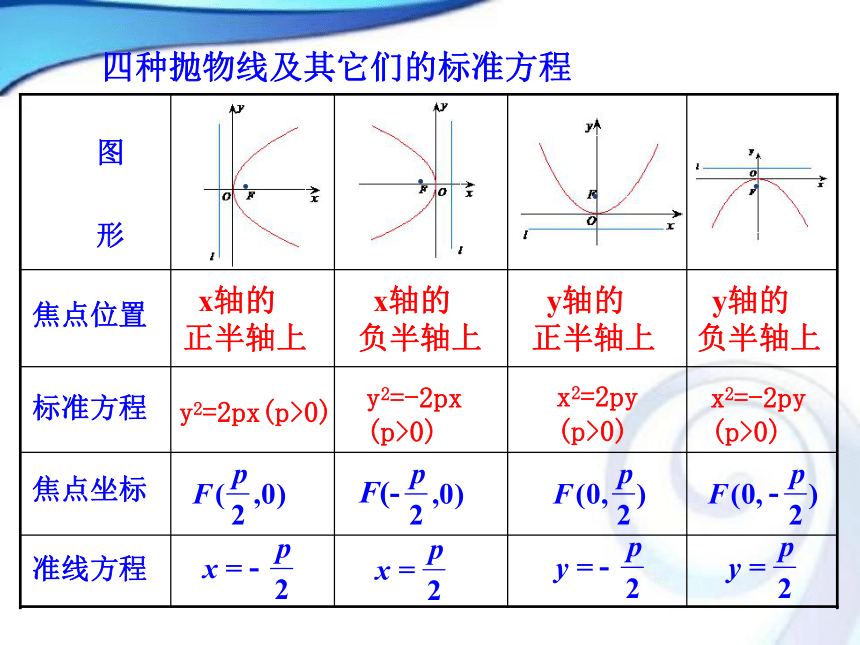
形 四种抛物线及其它们的标准方程 x轴的
正半轴上 x轴的
负半轴上 y轴的
正半轴上 y轴的
负半轴上y2=2px(p>0)y2=-2px (p>0)x2=2py (p>0)x2=-2py (p>0)....(1)若一次项的变量为X(或Y),则焦点就在X轴(或Y轴)上; 如何判断抛物线的焦点位置,开口方向?(2)一次项的系数的正负决定了开口方向 即:焦点与一次项变量有关;正负决定开口方向! 【总结提升】【即时小测】
1.抛物线y2=20x的焦点坐标是 ( )
A.(10,0) B.(5,0) C.(0,10) D.(0,5)
【解析】选B.因为2p=20,所以p=10,故 =5,且焦点在x
轴正半轴上.2.抛物线y2=ax(a≠0)的焦点到其准线的距离是( )
【解析】选B.由已知焦点到准线的距离为p= 3.抛物线y=2x2的准线方程为 .
【解析】化方程为标准方程形式为x2= y,故 ,开
口向上,所以准线方程为y=- .
答案:y=- 4.抛物线y=ax2的准线方程是y=2,则a的值为 .
【解析】将y=ax2化为标准方程形式得x2= y,
即 =2,p=4,- =2p=8,所以a=- .
答案:- 【知识探究】
探究点 抛物线的定义与标准方程
1.在抛物线定义中,若去掉条件“l不经过点F”,点的轨迹还是抛物线吗?
提示:不一定是抛物线.当直线l经过点F时,点的轨迹是过定点F且垂直于定直线l的一条直线;l不经过点F时,点的轨迹是抛物线. 2.抛物线的标准方程中p的几何意义是什么?
提示:p的几何意义是焦点到准线的距离.
3.确定抛物线的标准方程时,一般需要确定几个量?
提示:确定两个量,一个是p,另一个是一次项系数的正负.【归纳总结】
1.对抛物线定义的两点说明
(1)定直线l不经过定点F.
(2)定义中包含三个定值,分别为一个定点,一条定直线及一个确定的比值.2.抛物线标准方程的特点
(1)是关于x,y的二元二次方程.
(2)p的几何意义是焦点到准线的距离.3.四种位置的抛物线的标准方程的对比
(1)共同点:
①原点在抛物线上;
②焦点在坐标轴上;
③焦点的非零坐标都是一次项系数的 .(2)不同点:
①焦点在x轴上时,方程的右端为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2.
②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)负半轴上,方程右端取负号.特别提醒:
1.平面内到一定点距离与到一定直线距离相等的点的轨迹不一定是抛物线.
2.注意每种情况下的焦点与准线方程的对应关系.【例1】(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程.
(2)已知抛物线的焦点是F(0,-2),求它的标准方程.解:(1)因为p=3,故抛物线的焦点坐标为 ,
准线方程为(2)因为抛物线的焦点在y轴的负半轴上,且 故所求抛物线的标准方程为x2=-8y.1.根据下列条件写出抛物线的标准方程.
(1)焦点是(0,-3);
(2)准线是 .
2.求下列抛物线的焦点坐标与准线方程.
(1)y=8x2;
(2)x2+8y=0.x2=-12yy2=2x【总结提升】(1)用待定系数法求抛物线标准方程,应
先确定抛物线的形式,再求p值.(2)求抛物线的
焦点坐标和准线方程要先化成抛物线的标准方程.【变式练习】【例2】一种卫星接收天线的轴截面如图(1)所示.卫
星波束呈近似平行状态射入轴截面为抛物线的接收天
线,经反射聚集到焦点处.已知接收天线的口径(直径)
为4.8m,深度为0.5m,试建立适当的坐标系,求抛物线
的标准方程和焦点坐标.,即p=5.76.解:如图(2),在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合.设抛物线的标准方程是 所以,所求抛物线的标准方程是 ,焦
点坐标是(2.88,0). 由已知条件可得,点A的坐标是(0.5,2.4),代入方程得(2).F【变式练习】点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,
则点M的轨迹方程为 ..OFl-5-4xy.M【解题关键】:
看出M点与F的距离与它到
直线:x+4=0的距离相等,
然后根据抛物线的定义求
出P,写出方程即可.4C2.设抛物线y2=8x上一点P到y轴的距离是4,则
点P到该抛物线焦点的距离是( )
A.12 B.4 C.6 D.8 C3.已知动圆M经过点A(3,0),且与直线l:x=-3相切,求动圆圆心M的轨迹方程.解析:设动点M(x,y),设圆M与直线l:x=-3的切点为N,则|MA|=|MN|,即动点M到定点A和定直线l:x=-3的距离相等,所以点M的轨迹是抛物线,
且以A(3,0)为焦点,以直线l:x=-3为准线,
所以 =3,所以p=6.
所以圆心M的轨迹方程是y2=12x.抛
物
线
2.4.1 抛物线及其标准方程 生活中存在着各种形式的抛物线抛物线的生活实例 我们知道,二次函数y=ax2+bx+c(a≠0)的图象是一条抛物线,而且研究过它的顶点坐标、对称轴等问题.那么,抛物线是怎么定义的,方程是什么呢?探究点1 抛物线的定义MHFE思考:如图,点F是定点,l是不经过点F的定直线.H是l上任意一点,经过点H作MH⊥l,线段FH的垂直平分线m交MH于点M.拖动点H,观察点M的轨迹.你能发现点M满足的几何条件吗?m抛物线的定义: 在平面内,与一个定点F和一条定直线l(l不经过点F) 距离相等的点的轨迹叫做抛物线.|MF|=d焦点d准线点F叫做抛物线的焦点,
直线l 叫做抛物线的准线.明确了抛物线的定义,你能根据定义求出抛物线的
标准方程吗?一条经过点F且垂直于l 的直线想一想:定义中当直线l 经过定点F,则点M的轨迹是什么?······以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.KOFMl···(x,y)设M(x,y)是抛物线上任意一点,H点M到l的距离为d.d由抛物线的定义,抛物线就是点的集合探究点2 抛物线的标准方程两边平方,整理得KOFMl···(x, y)Hd其中p为正常数,它的几何意义是: 焦点到准线的距离.方程 y2 = 2px(p>0)表示焦点在x轴正半轴上的抛物线. 若抛物线的开口分别朝左、朝上、朝下,你能根据上述办法求出它的标准方程吗?O准线方程焦点坐标标准方程焦点位置 图
形 四种抛物线及其它们的标准方程 x轴的
正半轴上 x轴的
负半轴上 y轴的
正半轴上 y轴的
负半轴上y2=2px(p>0)y2=-2px (p>0)x2=2py (p>0)x2=-2py (p>0)....(1)若一次项的变量为X(或Y),则焦点就在X轴(或Y轴)上; 如何判断抛物线的焦点位置,开口方向?(2)一次项的系数的正负决定了开口方向 即:焦点与一次项变量有关;正负决定开口方向! 【总结提升】【即时小测】
1.抛物线y2=20x的焦点坐标是 ( )
A.(10,0) B.(5,0) C.(0,10) D.(0,5)
【解析】选B.因为2p=20,所以p=10,故 =5,且焦点在x
轴正半轴上.2.抛物线y2=ax(a≠0)的焦点到其准线的距离是( )
【解析】选B.由已知焦点到准线的距离为p= 3.抛物线y=2x2的准线方程为 .
【解析】化方程为标准方程形式为x2= y,故 ,开
口向上,所以准线方程为y=- .
答案:y=- 4.抛物线y=ax2的准线方程是y=2,则a的值为 .
【解析】将y=ax2化为标准方程形式得x2= y,
即 =2,p=4,- =2p=8,所以a=- .
答案:- 【知识探究】
探究点 抛物线的定义与标准方程
1.在抛物线定义中,若去掉条件“l不经过点F”,点的轨迹还是抛物线吗?
提示:不一定是抛物线.当直线l经过点F时,点的轨迹是过定点F且垂直于定直线l的一条直线;l不经过点F时,点的轨迹是抛物线. 2.抛物线的标准方程中p的几何意义是什么?
提示:p的几何意义是焦点到准线的距离.
3.确定抛物线的标准方程时,一般需要确定几个量?
提示:确定两个量,一个是p,另一个是一次项系数的正负.【归纳总结】
1.对抛物线定义的两点说明
(1)定直线l不经过定点F.
(2)定义中包含三个定值,分别为一个定点,一条定直线及一个确定的比值.2.抛物线标准方程的特点
(1)是关于x,y的二元二次方程.
(2)p的几何意义是焦点到准线的距离.3.四种位置的抛物线的标准方程的对比
(1)共同点:
①原点在抛物线上;
②焦点在坐标轴上;
③焦点的非零坐标都是一次项系数的 .(2)不同点:
①焦点在x轴上时,方程的右端为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2.
②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)负半轴上,方程右端取负号.特别提醒:
1.平面内到一定点距离与到一定直线距离相等的点的轨迹不一定是抛物线.
2.注意每种情况下的焦点与准线方程的对应关系.【例1】(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程.
(2)已知抛物线的焦点是F(0,-2),求它的标准方程.解:(1)因为p=3,故抛物线的焦点坐标为 ,
准线方程为(2)因为抛物线的焦点在y轴的负半轴上,且 故所求抛物线的标准方程为x2=-8y.1.根据下列条件写出抛物线的标准方程.
(1)焦点是(0,-3);
(2)准线是 .
2.求下列抛物线的焦点坐标与准线方程.
(1)y=8x2;
(2)x2+8y=0.x2=-12yy2=2x【总结提升】(1)用待定系数法求抛物线标准方程,应
先确定抛物线的形式,再求p值.(2)求抛物线的
焦点坐标和准线方程要先化成抛物线的标准方程.【变式练习】【例2】一种卫星接收天线的轴截面如图(1)所示.卫
星波束呈近似平行状态射入轴截面为抛物线的接收天
线,经反射聚集到焦点处.已知接收天线的口径(直径)
为4.8m,深度为0.5m,试建立适当的坐标系,求抛物线
的标准方程和焦点坐标.,即p=5.76.解:如图(2),在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合.设抛物线的标准方程是 所以,所求抛物线的标准方程是 ,焦
点坐标是(2.88,0). 由已知条件可得,点A的坐标是(0.5,2.4),代入方程得(2).F【变式练习】点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,
则点M的轨迹方程为 ..OFl-5-4xy.M【解题关键】:
看出M点与F的距离与它到
直线:x+4=0的距离相等,
然后根据抛物线的定义求
出P,写出方程即可.4C2.设抛物线y2=8x上一点P到y轴的距离是4,则
点P到该抛物线焦点的距离是( )
A.12 B.4 C.6 D.8 C3.已知动圆M经过点A(3,0),且与直线l:x=-3相切,求动圆圆心M的轨迹方程.解析:设动点M(x,y),设圆M与直线l:x=-3的切点为N,则|MA|=|MN|,即动点M到定点A和定直线l:x=-3的距离相等,所以点M的轨迹是抛物线,
且以A(3,0)为焦点,以直线l:x=-3为准线,
所以 =3,所以p=6.
所以圆心M的轨迹方程是y2=12x.抛
物
线
