人教A版高中数学选修2-12.2.2椭圆的简单几何性质课件(共21张PPT)
文档属性
| 名称 | 人教A版高中数学选修2-12.2.2椭圆的简单几何性质课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 585.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-07 00:00:00 | ||
图片预览





文档简介
课件21张PPT。2.2.2 椭圆的简单几何性质
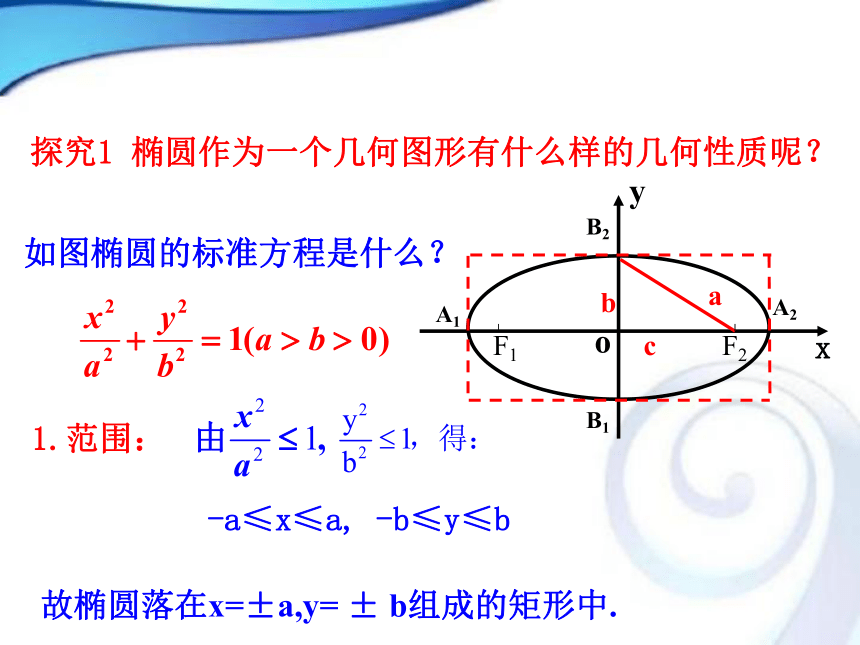
探究1 椭圆作为一个几何图形有什么样的几何性质呢?1.范围:
-a≤x≤a, -b≤y≤b
故椭圆落在x=±a,y= ± b组成的矩形中.如图椭圆的标准方程是什么?x2.椭圆的对称性:在方程中,把 换成 ,
方程不变,说明:
椭圆关于 轴对称;
椭圆关于 轴对称;
椭圆关于 点对称;
坐标轴是椭圆的对称轴,
原点是椭圆的对称中心,又叫做椭圆的中心.x-xxy(0,0)y -yx -x
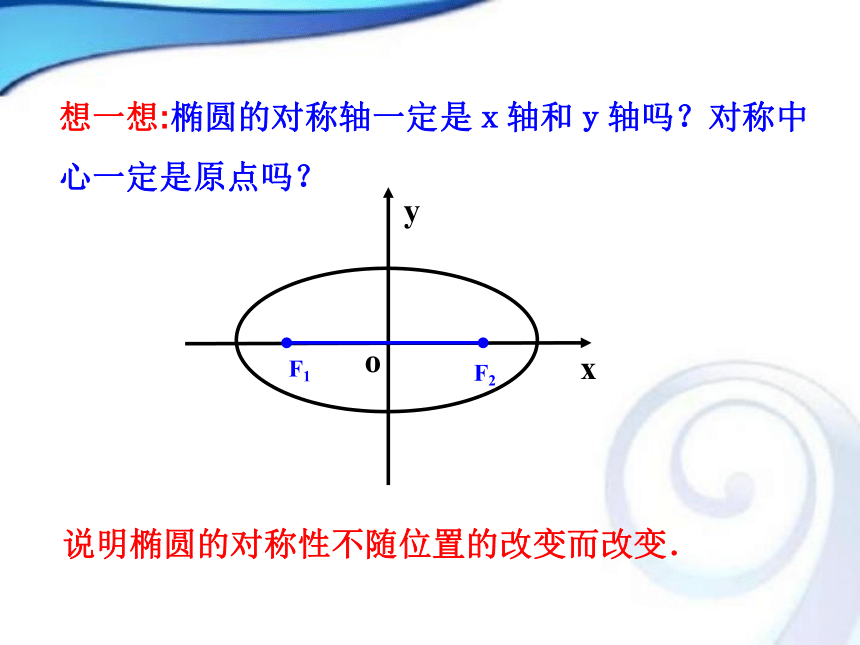
y -y Q(-x,y)P(x,y)M(x,-y)N(-x,-y)想一想:椭圆的对称轴一定是x轴和y轴吗?对称中
心一定是原点吗? oxy说明椭圆的对称性不随位置的改变而改变.椭圆顶点坐标为:3.顶点与长短轴:椭圆与它的对称轴的四个
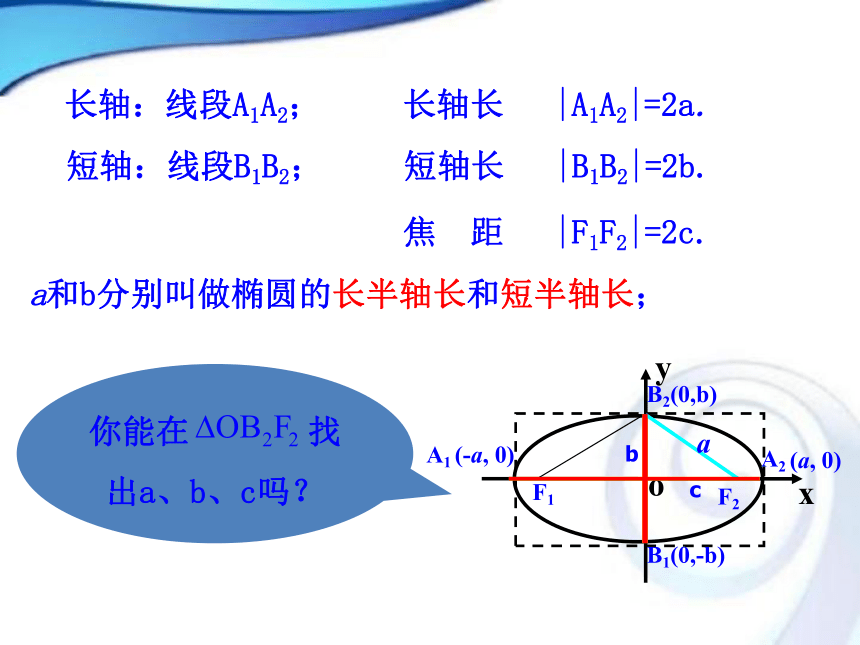
交点——椭圆的顶点.回顾:焦点坐标(±c,0) oxyA2(a, 0)A1(-a, 0)B2(0,b)B1(0,-b)你会求焦点在y轴的椭圆的顶点吗?长轴:线段A1A2;长轴长 |A1A2|=2a.短轴:线段B1B2;短轴长 |B1B2|=2b.焦 距 |F1F2|=2c.a和b分别叫做椭圆的长半轴长和短半轴长;B2(0,b)B1(0,-b)bac4.离心率:因为a>c>0,所以0 < e <1.椭圆的焦距与长轴长的比 叫做椭圆的离心率,用e离心率越大,椭圆越扁
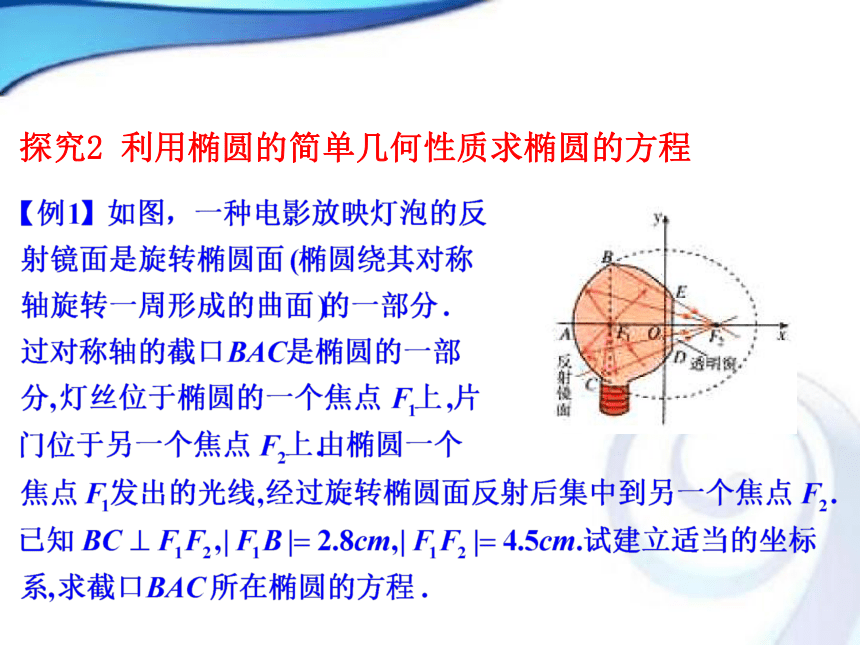
离心率越小,椭圆越圆表示,即(c,0)、(?c,0)(0,c)、(0,?c)(?a,0)、(0,?b)|x|? a |y|? b|x|? b |y|? a关于x轴、y轴、原点对称(?b,0)、(0,?a)【总结提升】焦点在y轴上的椭圆的几何性质又如何呢?xA2B2F2yOA1B1F1yOA1B1xA2B2F1F2( 0 < e < 1 )探究2 利用椭圆的简单几何性质求椭圆的方程解:待定系数法解:求轨迹方程的步骤?所以,点M 的轨迹是长轴长、短轴长分别为10、6的椭圆.已知椭圆的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定椭圆方程的形式;
(2)确立关于a,b,c的方程(组),求出参数
a,b,c;
(3)写出标准方程.【总结提升】问题2:怎么判断它们之间的位置关系?问题1:直线与圆的位置关系有哪几种?d>rd0?<0?=0几何法:代数法:直线与椭圆有什么样的位置关系,该如何判断呢?种类:相离(没有交点)
相切(一个交点)
相交(两个交点)能用几何法判断椭圆与直线的位置关系吗?探究3 直线与椭圆的位置关系问题3:直线与椭圆的位置关系如何判定?代数方法,联立方程转化思想方程思想1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程,消元得到一元二次方程(当二次项系数不为0时)
(1)△>0?直线与椭圆相交?有两个公共点;
(2)△=0?直线与椭圆相切?有且只有一个
公共点;
(3)△<0?直线与椭圆相离?无公共点.通法【总结提升】直线与椭圆的位置关系:x oy分析:作出直线l及椭圆(如图),
观察图形,可以发现,利用平行于
直线l且与椭圆只有一个交点的
直线,可以求得相应的最小距离.解:由直线l的方程与椭圆的方程可以知道,直线l与椭
圆不相交.设直线m平行于直线l,则直线m的方程可以
写成①②令方程②的根的判别式△=0,得③解方程③,得最大的距离是多少?椭圆的简单几何性质椭圆方程及性质的应用
探究1 椭圆作为一个几何图形有什么样的几何性质呢?1.范围:
-a≤x≤a, -b≤y≤b
故椭圆落在x=±a,y= ± b组成的矩形中.如图椭圆的标准方程是什么?x2.椭圆的对称性:在方程中,把 换成 ,
方程不变,说明:
椭圆关于 轴对称;
椭圆关于 轴对称;
椭圆关于 点对称;
坐标轴是椭圆的对称轴,
原点是椭圆的对称中心,又叫做椭圆的中心.x-xxy(0,0)y -yx -x
y -y Q(-x,y)P(x,y)M(x,-y)N(-x,-y)想一想:椭圆的对称轴一定是x轴和y轴吗?对称中
心一定是原点吗? oxy说明椭圆的对称性不随位置的改变而改变.椭圆顶点坐标为:3.顶点与长短轴:椭圆与它的对称轴的四个
交点——椭圆的顶点.回顾:焦点坐标(±c,0) oxyA2(a, 0)A1(-a, 0)B2(0,b)B1(0,-b)你会求焦点在y轴的椭圆的顶点吗?长轴:线段A1A2;长轴长 |A1A2|=2a.短轴:线段B1B2;短轴长 |B1B2|=2b.焦 距 |F1F2|=2c.a和b分别叫做椭圆的长半轴长和短半轴长;B2(0,b)B1(0,-b)bac4.离心率:因为a>c>0,所以0 < e <1.椭圆的焦距与长轴长的比 叫做椭圆的离心率,用e离心率越大,椭圆越扁
离心率越小,椭圆越圆表示,即(c,0)、(?c,0)(0,c)、(0,?c)(?a,0)、(0,?b)|x|? a |y|? b|x|? b |y|? a关于x轴、y轴、原点对称(?b,0)、(0,?a)【总结提升】焦点在y轴上的椭圆的几何性质又如何呢?xA2B2F2yOA1B1F1yOA1B1xA2B2F1F2( 0 < e < 1 )探究2 利用椭圆的简单几何性质求椭圆的方程解:待定系数法解:求轨迹方程的步骤?所以,点M 的轨迹是长轴长、短轴长分别为10、6的椭圆.已知椭圆的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定椭圆方程的形式;
(2)确立关于a,b,c的方程(组),求出参数
a,b,c;
(3)写出标准方程.【总结提升】问题2:怎么判断它们之间的位置关系?问题1:直线与圆的位置关系有哪几种?d>rd
相切(一个交点)
相交(两个交点)能用几何法判断椭圆与直线的位置关系吗?探究3 直线与椭圆的位置关系问题3:直线与椭圆的位置关系如何判定?代数方法,联立方程转化思想方程思想1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程,消元得到一元二次方程(当二次项系数不为0时)
(1)△>0?直线与椭圆相交?有两个公共点;
(2)△=0?直线与椭圆相切?有且只有一个
公共点;
(3)△<0?直线与椭圆相离?无公共点.通法【总结提升】直线与椭圆的位置关系:x oy分析:作出直线l及椭圆(如图),
观察图形,可以发现,利用平行于
直线l且与椭圆只有一个交点的
直线,可以求得相应的最小距离.解:由直线l的方程与椭圆的方程可以知道,直线l与椭
圆不相交.设直线m平行于直线l,则直线m的方程可以
写成①②令方程②的根的判别式△=0,得③解方程③,得最大的距离是多少?椭圆的简单几何性质椭圆方程及性质的应用
