数学之神──阿基米德 教案 (7)
文档属性
| 名称 | 数学之神──阿基米德 教案 (7) |

|
|
| 格式 | zip | ||
| 文件大小 | 407.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-06 00:00:00 | ||
图片预览




文档简介
《数学之神—阿基米德》
教学目标分析:
1、了解阿基米德的主要数学成就。
2、理解平衡法,并将其灵活运用于对球体体积的计算。
3、激发学生的求知欲,培养严谨的学习态度,培养积极进取的精神
重难点分析:
重点:了解阿基米德的主要数学成就
难点:理解平衡法。
教学准备:多媒体课件
教学过程:
一、知识讲解:
(一)导入:
金冠——阿基米德原理的发现
叙拉古的海厄罗王的政治威望及权势日益提高,为了报答诸神的德泽,他决定建造一个华贵的神龛,内装一个纯金的王冠,作为谢恩的奉献物 金匠如期完成了任务,理应得到奖赏.这时有人告密说金匠偷去一部分金子,以等重的银子掺入.国王甚为愤怒,但又无法判断是否确有其事.便请素称多能的阿基米德来鉴定一下,他也一时想不出好办法来.正在苦闷之际,他到公共浴室去洗澡,当浸入装满水的浴盆去的时候,水漫溢到盆外,而身体顿觉减轻.于是豁然开朗,悟到不同质料的物体,虽然重量相同,但因体积不同,排去的水必不相等.根据这一道理,不仅可以判断王冠是否掺有杂质,而且知道偷去黄金的份量.这一发现非同小可,阿基米德高兴得跳了起来,赤身奔回家中准备实验,口中不断大呼“尤里卡!尤里卡!”(Eureka,意思是“我找到了”.)
这问题可解释如下:设王冠重W,其中金与银分别重W1,W2,而W=W1+W2分别取重为W与W1的纯金放入水中,设排去水的重各 的银放入水中,设排去水的重量各为F2与y,于是W∶W2=F2∶y,由此推得F(W1+W2)=F1W1+F2W2,即用实验可求出F,F1,F2,即可算出银与金之比值.如F=F1,说明没有掺银.实际情况是两者不等,从而揭穿了金匠的劣行.
经过仔细实验和反复思考,将经验上升为理论,他终于发现了流体静力学的基本原理——阿基米德原理
(二)新科教授
1、阿基米德简介
阿基米德(Archimedes) 公元前287年生于西西里岛(Sicilia,今属意大利)的叙拉古(Sracusa,—译锡拉库萨);公元前212年卒于叙拉古.
阿基米德早年曾在当时希腊的学术中心亚历山大跟随欧几里得的门徒学习,对欧几里得数学进一步的发展作出了一定的贡献.阿基米德也算是亚历山大学派的成员,他的许多学术成果就是通过和亚历山大的学者通信往来保存下来的.后人对阿基米德给以极高的评价说:任何一张列出有史以来三个最伟大的数学家的名单中,必定会包括阿基米德,另外两个通常是牛顿和高斯.不过以他们的丰功伟绩和所处的时代背景来对比,拿他们的影响当代和后世的深邃久远来比较,还应首推阿基米德.
2、主要著作
阿基米德留下的数学著作不下10种,多数为希腊文手稿,也有的是13世纪以后从希腊文译成拉丁文的手稿.著作的题例,深受欧几里得《几何原本》的影响,先设立若干定义和假设,再依次证明各个命题.各篇独立成章,虽然不象《原本》那样浑然一体,但所言均有根据,论证也是严格的.现按海伯格本的顺序(为希思本所沿用)列举如下:
《论球与圆柱》《圆的度量》《劈锥曲面与回转椭圆体》《论螺线》《平面图形的平衡或其重心》 《数沙器》 《抛物线图形求积法》 《论浮体》 《引理集》《群牛问题》
在本世纪初还发现阿基米德的一封信,这信非常重要,它记录了阿基米德研究问题的独特思考方法,后来以《阿基米德方法》(The method of Archimedes,简称《方法》)的标题发表出来.
《方法》包括15个命题.一开头是写给埃拉托塞尼的信用来说明本篇的主要内容,相当于序言.下面,以命题1为例,阐明阿基米德的思想方法.为了便于了解,暂用现代的术语和符号来推导.
设D是抛物线弧ABC的弦AC的中点,过D作直线平行于抛物线的轴OY,交抛物线于B.要证明的是抛物弓形ABCD的面积等于△ABC面积的 4/3.当时已经知道过B的切线平行于AC,即B是弓形的顶点(在ABC弧上与AC距离最远的点).命题结论的另一种说法是: 抛物弓形的面积,是等底等高的三角形的4/3.用解析几何来分析,设抛物线方程是
y=ax2 (1)
A,C的横坐标分别是x1,x2,则AC的方程是 y=ax1x+ax2x-ax1x2 (2)
过C点的切线CF的方程是
延长DB交CF于E,不难证明,B是ED的中点.事实上,将D,B,
坐标,依次是
由此知B是D、E中点.
作AF‖OY,交CF于F.延长CB交AF于K,则K是FA的中点.再取KH=KC,过AC上任意点M作MQ‖OY,交CK于P,交CF于Q,交抛物线于N.将M的横坐标x2分别代入(2)、(1)、(3)得到M,N,Q的纵坐标
ym=ax1x0+ax2x0-ax1x2,
于是有:
3、各篇著作的主要内容
(1)《论球与圆柱》
例第5个公理,这就是后来以阿基米德的名字命名的公理:如果两条线段或两个面、两个立体不相等,就可以在两者之差的上面,加上它的本身,一次一次加上去,使得每一个预先给定的同类量都被超过.在现代分析学中常用的说法是:对于任意二正实数 a,b,必存在自然数n,使得na>b.
从这些定义和公理出发,推导出上卷44个,下卷9个命题.多次使用阿基米德公理及反证法(归谬法),如要证A=B,则证明A>B及A<B均导致矛盾.以下面的命题为例来说明.
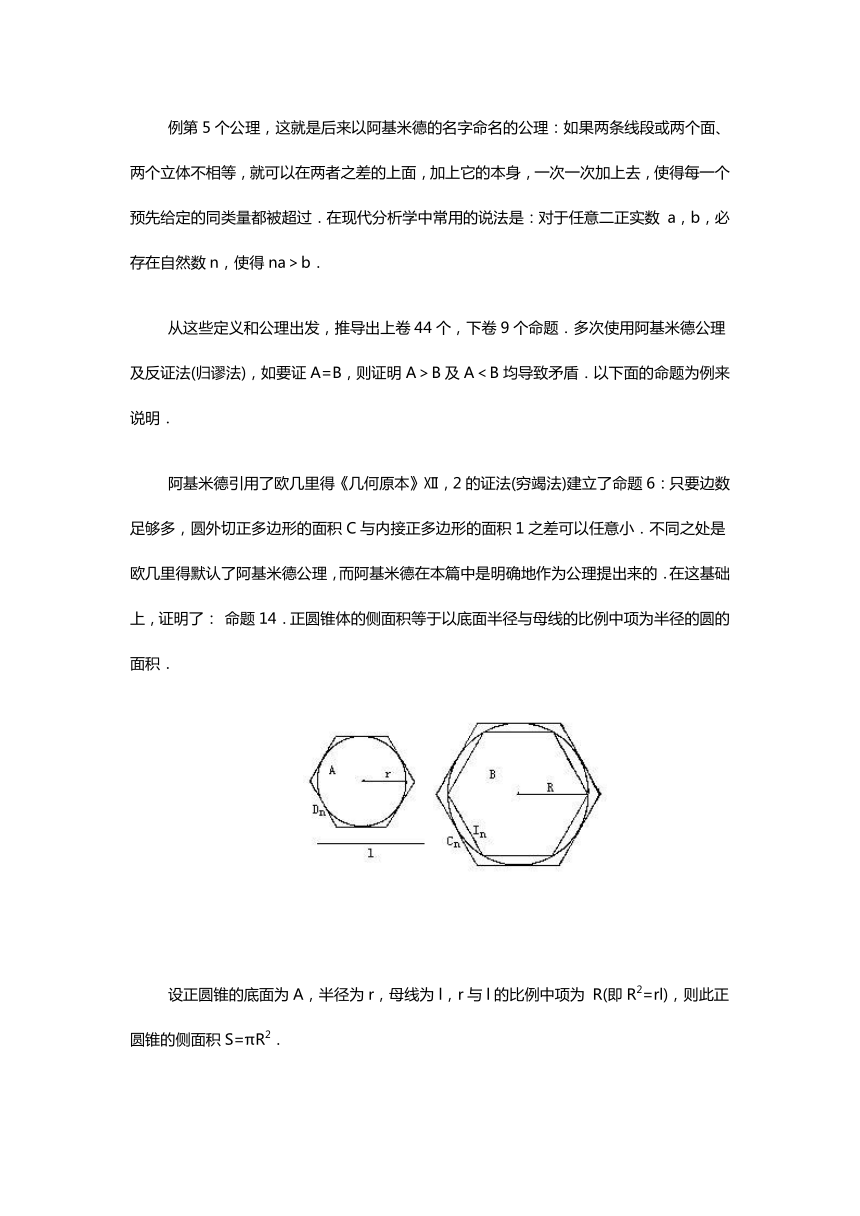
阿基米德引用了欧几里得《几何原本》Ⅻ,2的证法(穷竭法)建立了命题6:只要边数足够多,圆外切正多边形的面积C与内接正多边形的面积1之差可以任意小.不同之处是欧几里得默认了阿基米德公理,而阿基米德在本篇中是明确地作为公理提出来的.在这基础上,证明了: 命题14.正圆锥体的侧面积等于以底面半径与母线的比例中项为半径的圆的面积.
设正圆锥的底面为A,半径为r,母线为l,r与l的比例中项为 R(即R2=rl),则此正圆锥的侧面积S=πR2.
以R为半径作圆B,其面积为πR2,现要证明S=B=πR2.用反证法,设S>B.根据命题6,可作B的外切正多边形Cn(同时表示其面积,下同)与内接正边形In,使得
又作底面A的相同边数的外切正多边形Dn,其周长记作Pn.以Dn为底,
Dn,Cn是相似的,其比等于对应线段平方之比,
由此知Cn=Ln,代入上面的不等式有
这是不合理的,因为圆锥侧面积S小于其外切棱锥侧面积Ln,而圆B大于其内接多边形面积In.同理可证S<B也是不合理的,故S=B=πR2.现在常用的形式是S=πrl.
下面较著名的命题还有命题33.球面积等于它的大圆面积的4倍.
命题34.球体积等于以它的大圆为底、它的半径为高的圆锥体积的4倍.推论:以球的大圆为底、球直径为高的圆柱的体积与表面积分别是球的体积与表面积的3/2.这命题在《方法》中已提出,此处用反证法加以证明.
命题35—44研究了球缺、球冠及球心角体(球扇形)的表面积及体积.
下卷9个命题主要讨论球缺,好几个是作图题.命题2给出球缺的体积.命题4在历史上占有特殊的地位.它要求用平面将一个球截成两部分,使这两部分体积之比等于给定的比.
设球半径为r,所分成的两个球缺的高各为h及2r-h,公共底的半
可改写为
记x=2r-h,a=3r,又将右端的常数写成bc2,上式简写成x2(a-x)=bc2.
此问题的解相当于用几何方法去解这个3次方程.阿基米德说他将在后面给出分析与综合的解法,但现存本未见,大概已失传.后来欧托基奥斯(5世纪时)找到一些残页,是用多利安方言(阿基米德惯用的方言)写的手稿,上有这问题的解法,他认为是属于阿基米德的.解法的要点是求两条圆锥曲线的交点.一条是抛物线
另一条是双曲线(a-x)y=ab.残页还讨论了方程可解的条件,这
时,还比较了狄俄尼索多罗(Dionysodo-rus,公元前3世纪—公元前2世纪,居住在小亚细亚地区)以及狄俄克利斯(Diocles,约公元前190年)对此问题的解法.
(二)《圆的度量》,其中只有3个命题.
命题1.圆的面积等于一个以其周长及半径作两个直角边的直角三角形的面积.
更简单的说法是:圆面积等于半径乘半周长.这正是中国《九章算术》的说法:“半周长半径相乘得积步”.或刘徽(公元263年)注的说法:“半周乘半径为圆幂”.
但在古希腊,自从毕达哥拉斯学派发现不可公度量以后,每一条线段是否都有长度就成了问题.因此在几何学家的著作中,极力避免两条线段长相乘的说法,宁愿说成由两线段构成的矩形或三角形的面积.
证明仍用穷竭法.圆半径为r,周长为C,面积为S.以C,r为两直角边作直角三角形,设面积为K.现证明S=K.用反证法,假定S>K,作边数足够多的内接正多边形In,使其面积In与圆面积S之差
S-In<S-K,
于是有
In>K.
这是不合理的,因为In的边心距d<r,而In的周长小于C,故In应<K.同理作外切正多边形,可证S<K也导致矛盾,从而有S=K.
命题2.圆面积与外切正方形面积之比为11∶14.
命题应该放在命题3的后面,也许是后人抄错了或阿基米德别有用意.
这就是有名的阿基米德圆周率的出处.欧几里得在《原本》中讨论了很多圆的性质,但却完全没有提到圆周率的值及圆面积、圆周长的计算法.阿基米德弥补了这一不足,并在科学上首次创用上、下界来确定一个量的近似值,还提供了误差的估计。
他在推导中使用了一个不等式
分数的渐近分数.它具有这样的特性,以265/153为例,在一切分母
的性质.阿基米德是怎样得到这些分数的?这引起后人的极大兴趣.仅从17世纪以来,就至少有十几种不同的推测.较多的意见认为是利用了不等式
左右各平方,便可证其成立.试推演如下:
取右端
于是有
本命题主要的推导思想如下:设O是圆心,OA是半径,作
∠AOB=30°,
过A作切线AB交OB于B.则
两式左右相加得
作∠AOB的平分线OC,则
左端分母与右端分子交换,再由前面的不等式,有
或
由上面的不等式立刻推出圆外切正6边形、正12边形的周长与直径比值的上界.同样,计算内接正多边形的边长,可以确定比值的下界.再利用比例关系及勾股定理,重复上述手续,一直算到96边形,最后得到
一切分母不大于71的分数中它是最接近π的.比它更接近π的分数有
①①见梁宗巨,祖冲之密率的优越性,《辽宁师范大学学报》增刊(数学史专辑),1986,p.6.
分母都大于71,除了最后一个外,都不是连分数的渐近分数.
(三)《劈锥曲面与回转椭圆体》
共32个命题,研究椭圆的面积以及回转圆锥曲线体被平面截取部分的体积等.证明的方法是穷竭法,十分接近今天的积分法思想.当时还没有“抛物线”(parabola)等名称,早期的希腊数学家如门奈赫莫斯(Menaechmus,公元前4世纪),用平面去截三种不同的直圆锥面,产生三种圆锥曲线.令平面与直圆锥的母线垂直,当圆锥的顶角(母线所张的最大角度)是直角时,截口叫做“直角圆锥截线”(section of a right-angled cone),现在叫抛物线;当顶角是锐角时,叫“锐角圆锥截线”(section of an acute-angledcone),现叫椭圆;当顶角是钝角时,叫“钝角圆锥截线”(section ofan obtuse-angled cone),现叫双曲线.欧几里得和阿基米德一直沿用这些旧名称,为简单起见,改用今名.
本篇一开头先给出两个引理,以备后面证明之用.第1个是等差数列求和公式,写成不等式
2(a+2a+3a+…+na)>n2a
>2[a+2a+3a+…+(n-1)a].
如用求和公式,左端是n(n+1)a,右端是(n-1)na,不等式成立是明显的.
第2个是自然数平方和公式,先证明
(n+1)(na)2+a(a+2a+3a+…+na)
=3[a2+(2a)2+(3a)2+…+(na)2],
由此可知
a2+(2a)2+(3a)2+…+(na)2
写成不等式
3Sn-1a2<n3a2<3Sna2.
下面以一个较简单的命题来阐明阿基米德的证题思想.为了便于理解,改用现代的术语和符号.
命题21.回转抛物体被垂直于轴的平面所截取的部分的体积等于同底等高的圆锥体的3/2.
抛物线AOB(不妨设方程为y=x2)绕其轴OC回转,产生回转抛物体.求被垂直于OC的平面ACB所截取的部分的体积V.将OC用分点O,C1,C2,…,Cn-1,Cn(=C)分成n等分,过这些分点作垂直于OC的平面将所求的体积分成n个小薄片.每一个小薄片介于一个内接圆柱与一个外接圆柱之间.例如E1H2及A1F2回转后就产生C1,C2间的小薄片的内接与外接圆柱.又每一个外接圆柱与紧接着上面的一个内接圆柱(如A0F1与E1H2回转产生的圆柱)相等.
=In.这是根据前面引理得出的不等式.现证明V=V*,否则,如V>V*,
Sn-In<V-V*,
这是不合理的,因Sn>V而In<V*.同理可证V<V*也导致矛盾,故
其余各命题虽然都比这复杂,但基本思路是差不多的.除了没有取极限这一步骤之外,基本思想和现代积分是一致的.
(四)《论螺线》
共28个命题,前10个是关于圆及切线的各种比例关系的.命题11重新证明了自然数平方和的不等式,这在《劈锥曲面与回转椭圆体》中是作为引理提出的:
接着给出螺线(现在称为“阿基米德螺线”)的定义.
一条射线绕其固定端点匀速旋转,同时有一动点从端点出发沿射线匀速运动,那么这动点就描绘出一条平面螺线(spiral).射线开始时的位置叫做始线(OA),固定端点叫做原点(O).旋转一圈所产生的螺线与始线所包围的面积叫做“第1面积”(first area).
现在在解析几何中螺线的极坐标方程是r=aθ,旋转一圈后动点到达A点,OA=2πa,以OA为半径的圆叫做“第1圆”.
命题21以后的几个命题探讨螺线所围的面积,命题24证明了“第1面积”S等于“第1圆”面积的1/3,即
螺线的内接与外接扇形.例如第3等分的内接扇形是ON2P3,外接扇形是OM2N3.设全部外接扇形面积的总和是Cn,内接扇形面积的总和是In,则Cn>S>In又根据自然数平方和的不等式,并注意到弓形面积公,有
可以任意小.
应用前面多次用过的反证法,可证S=S*.否则,如S>S*,则可使
Cn-In<S-S*,
这是不合理的,因外接扇形面积总和>S,而In<S*.同样S<S*也是不合理的.于是得到
命题13—20研究了螺线的切线,给出作图方法及种种性质.没有发现阿基米德有微分法的思想(那怕是粗浅的),那么他是怎样得到切线的作法的?这有趣而且带有关键性的问题引起后人的注意.有些学者认为是运用了运动学的原理.射线作匀角速运动,而动点在射线上作匀速运动,两个速度按平行四边形法则所得到的合速度方向就是切线方向.如果这推测正确的话,那么这就是古代属于微分法的罕见的例子.
(五)《平面图形的平衡或其重心》
分两卷,卷Ⅰ先给出7个公理,都是显而易见之理.例如1.等重的物体放在相等的距离上(各在杠杆一端,与支点等距),则处于平衡状态;等重的物体放在不相等的距离上则不平衡,向距离远的一端倾斜.
2.放在一定距离上的重物处于平衡状态时,若在其中的一个重物上加一点重量,则失去平衡,要向加重量的一端倾斜.
5.相似图形的重心,也处在相似的位置上.
从这些公理出发,导出了著名的杠杆定律:
命题6,7.若两重物平衡,则所处的距离(与支点的距离)与重量成反比.
证明是分可公度量与不可公度量两种情形来讨论的.下面的8个命题找出平行四边形、三角形以及梯形的重心.
卷2的10个命题集中研究了抛物弓形和它的一部分的重心.方法是作一系列的内接三角形,逐步去逼近所讨论的图形.
(六)《数沙器》
这是阿基米德遗留下来的唯一的算术著作,也可能是最后的一种.那时海厄罗王已去世(公元前216年),他的儿子吉伦(Gel-on)继承王位,阿基米德也已年逾古稀.这篇文章是递交给吉伦王的.
文章首先表明写作的目的,是要纠正有些人的错误观点,他们认为世界上的沙子是无穷的,即使不是无穷,也没有一个可以写出来的数超过沙子的数.阿基米德指出,任何大的数都可以表示出来.
全文只有一个定理,实际相当于现今的指数法则
Am·An=Am+n
他先给出地球、月球、太阳大小的估计,进而计算沙粒的数目.
1.地球的周长不大于3×106个“斯达地”(stadium,复数stadia).斯
的周长是5.55×105公里,而实际是40000公里.
2.地球直径大于月球直径,太阳直径大于地球直径.
3.太阳直径是月球直径的30倍.(实际是400倍)
这些估计数字和实际出入很大,不过他自己也说只是一种假定.接着推出
“宇宙”(相当于太阳系)直径<1010斯达地.
当时希腊用字母表示数字,最大的单位是“万”(10000,myri-ad),
表示加大10000倍.
阿基米德以万为基础,建立新的记数法,使得任何大的数都能表示出来.
从1起到1亿(原文是万万,myriad myriads,按中文的习惯改称为亿)叫做第1级(first order)数;以亿(108)为第2级数的单位,从亿(108)到亿亿(108)2叫第2级数;再以亿亿(108)2为单位,直到亿亿亿(108)3叫第3级数;照此类推,直到第1亿级数的最后一
原文全用语言来叙述,没有创设记数符号,他是否在别的地方使用了符号不得而知.为了叙述简明,这里用P表示亿亿(108)108.从1到P叫做第1周期(first period).下面列成表:
第1周期
第1级 从1到108
第2级 从108到(108)2
第2周期
第1级 从P到P·108
第2级 从P·108到P·(108)2
第108周期
+1位.
阿基米德算出充满宇宙的沙数不过是1051,即使扩充到“恒星宇宙”,即以太阳到恒星的距离为半径的大球,也只能容纳1063个沙粒,远远小于前面列出的大数.
现今从理论上推测,可观察到的宇宙半径约为130亿光年,假想整个充满了具有最小可能体积的粒子(如质子),其数也不超过10125.也还不能和上述的大数相比.
阿基米德的记数方法还可以继续下去,他企图说明任何大的数都可以表示出来,现在目的业已达到.可惜他没有再进一步去改革整个的希腊记数制度.也许那时已进行或临近叙拉古保卫战,致使改革工作功亏一篑.
(七)《抛物线图形求积法》
在《方法》中、阿基米德利用力学原理,已经得到“抛物弓形面积是同底等高的三角形的4/3”的结论.但他认为这不算证明,在本篇中另外用完全不同于力学的几何方法去严格证明它.基本思想是穷竭法,作一系列的内接三角形去穷竭(逼近)弓形,最后用归谬法完成证明.
全篇24个命题,最后一个命题才是所要的结论,前面的都可以看作是引理.为了避免叙述的冗长,下面用解析几何来说明.
设抛物线方程为
y2=2x
在抛物线上任取两点P1(x1,y1),P2(x2,y2),不妨设y1>y2.过P1P2中点M作MV‖抛物线的轴OX,交抛物线于V,V是抛物弓形P1VP2的顶点,即过V的切线‖于P1P2,ΔP1VP2与弓形同底等高(命题1与18已证).现要证明弓形面积S是ΔP1VP2面积的4/3.
过VP1中点M1作M1Q1‖OX交抛物线于Q1,过P2V中点M2作
称ΔP1VP2为1级三角形,面积记作Δ1,ΔP1Q1V及ΔP2VQ2称为2
VQ2,Q2P2之上作4个3级三角形,其面积总和为Δ3,同样可证
这手续可以继续下去,直到作出n级三角形,其面积的总和
由此知
又
前面的命题已证明,内接三角形的级数越多,In越大,S-In越小,同时Δn也越小,以至小于任给的正数.
或
这与前面的不等式矛盾.
In>S
这也是不合理的,因In是内接三角形面积之和,应有In<S.综上所述,
(八)《论浮体》
这是古代第一部流体静力学著作,阿基米德因此而被尊为流体静力学的创始人.20世纪之前,本书只有莫贝克13世纪时的拉丁文译本,1906年,海伯格发现了羊皮纸上的希腊原文,但不完全.现传的本子是两种文字参照编成的.
卷上命题7给出著名的“阿基米德原理”:重于流体的固体,放在流体中,所减轻的重量等于排去流体的重量.这原理因和他解决王冠问题联系起来而脍炙人口.
卷下的10个命题相当详细地讨论了正回旋抛物体在流体中的稳定性,研究了不同的高与底的比、具有不同的比重及在流体中处于不同位置时这种立体的性态.在推理中运用了高度的计算技巧.
(九)《引理集》
只有阿拉伯文译本传下来,是15个初等几何的问题集.也许不是阿基米德的原著而是后人收集整理的,因为在文章中不止一次提到阿基米德的名字.其中提出一种被称为“皮匠刀”(shoe-maker’s knife)的图形,是三个半圆所包围的部分,两个小半圆外切,又同时内切于大半圆.这图形有许多奇妙的性质,如通过两小圆的外切点C,作CP⊥大圆直径AB(三个圆的直径是重合的)交大圆于P,则“皮匠刀”AGCBPA的面积等于以CP为直径的圆面积.又可以作两个小圆,分别切于CP、大圆及一个小圆,可证这两个小圆相等.设HE是‖于AB的一个小圆的直径,则切点F与H,A共线,F与E,B也共线.E是ΔABD的垂心,从A向DB作垂线,垂足I必落在大圆周上.又AE,HC必过切点G,等等。还有许多其他的性质.
命题8和3等分角问题有关.设AB是⊙O的任一弦,延长AB至C使BC等于圆的半径.联CO并延长之使交圆于E,D.求证
联OA,OB,只要证明∠AOE=3∠BOD即可.实际上∠AOE=∠OAC+∠OCA=∠OBA+∠OCA=∠BOC+2∠OCA=3∠BOD.
现将问题倒过来考虑.设有∠AOE,求它的三等分角.这就是古希腊的三大作图问题之一的“三等分任意角”问题.从理论上说用直尺和圆规是不可能解决的.受到本命题的启发,只要在直尺上加一个点,就能轻而易举地解决这历史难题.
在直尺ABC上记上一个点B,使B至尺端C的距离等于半径.现令尺通过A点,B在圆周上移动,当C落在直径的延长线EDC上时,作ABC直线,则∠C就是所求的三等分角.
当然这已不是欧几里得几何的尺规作图法,因为工具已经改变(即使只加一点!),而且不合作图公法.不过它说明了一个问题,有些初学者只知道三等分角是难题,但不知难在尺规的限制上,如不限于尺规、那真是易如反掌.
(十)《群牛问题》
阿基米德的论文向来是以命题的形式来表达的,而这篇的体例不同,它是用诗句写成的(原文见[7],p.203).标题是给埃拉托塞尼的信.胡尔奇(Hultsch)曾猜想这是阿基米德“显本领”(tour de force)之作,以此向亚历山大的学者们(特别是阿波罗尼奥斯)挑战.但它的真实性颇值得怀疑,“群牛问题”大概很早以前就已存在,阿基米德只是重新研究而已.诗句也未必出自他的手.内容如下:
太阳神赫利俄斯(Helios)有一大群牛在西西里岛草原上放牧.公牛和母牛各有4种颜色,各种头数之间的关系如下:令W,w分别表示白色公牛、母牛的头数;
X,x……………黑色……………;
Y,y……………黄色……………;
Z,z……………花色…………….
要求
个三角形.倒数第2个条件是含混的,原话是“黑色和白色的公牛可以合起来排成一个方形,长与宽是相等的”.有两种可能解释,一是长与宽的数目相等,即
W+X=n2(完全平方数);
另一是方形的两个边长相等,但由于牛的身长与体宽不一样,方形两个边的数目并不相等,条件成为①①这种解释也很牵强,因为要挤成一个正方形,还需要考虑身长与体宽的比,故右端不是任意两个正整数之积mn而是kn2(k是常数),这样问题并没有化简.
W+X=mn.
后一种情形较易解决,称为“较简问题”,而前一种情形称为“完全问题”.
“较简问题”已由Jul.Fr.武尔姆(Wurm)解决.“完全问题”在1880年为阿姆托尔(Amthor)所解决.即使较简问题,牛的总数也已达到5916837175686头之多!而完全问题导致2元2次方程
t2-4729494u2=1.
最小解牛的总数是7 766×10206544,位数超过20万!当时阿基米德未必解得出来.
其他工作
(一)半正多面体(semi-regular polyhedron)
帕波斯在《数学汇编》中记述阿基米德发现了13种半正多面体.各个面是若干个不同类的正多边形,但同一类的都相等.例如12个相等的正5边形和80个相等的三角形构成一个92面体;6个正8边形,8个正6边形,12个正方形构成26面体;26面体又可以由18个正方形和8个正三角形构成.如此等等.
(二)三角形面积公式
阿拉伯数学家比鲁尼(Abū’l Raihān Muhammad al-Bīrūnī,973—1050?)记述,阿基米德发现了用边表三角形面积的公式
s是三角形三边a,b,c之和之半,这公式通常归功于海伦(He-ron,62年前后),并称为海伦公式.
(三)正7边形作图法
另一个阿拉伯数学家塔比伊本库拉(Thābit ibn Qurra,826—901)指出,阿基米德发现正7边形的作图法.自然不是尺规作图,可惜方法已失传,
(四)天文学方面
阿基米德对天文学也深有研究,但著作没有留下来.西塞罗的书记载马塞勒斯攻占叙拉古时,曾获得两座阿基米德制作的天文仪器.一座是天球仪,上刻各个星座,后放置在神庙中.另一座为加卢斯(Gain Sulpicius Gallus,公元前166年为罗马执政官)所有.可称为天象仪(planetarium),借助机械或水力表演日、月、行星的运行,还可以演示日、月食.
(五)阿基米德螺旋泵
历史学家狄奥多罗斯(Diodorus Siculus,公元前1世纪)记载阿基米德在埃及时,发明一种螺旋水泵,被埃及人广泛使用.
结束语
历史上有的数学家勇于开辟新的园地,而缺乏缜密的推理,有的数学家偏重于逻辑证明,而对新领域的开拓却徘徊不前.阿基米德则兼有二者之长,他将惊人的独创与严格的论证融为一体,更善于将计算技巧与逻辑分析结合起来.正确地注意理论与实际的联系,常常通过实践直观地洞察到事物的本质,然后运用逻辑方法使经验上升为理论(如浮力问题),再用理论去指导实际工作(如发明抗敌器械).在严格性方面,实超过了15—17世纪的分析学家,他的理论比牛顿、莱布尼茨更加接近柯西、外尔斯特拉斯的ε-δ方法(例如阿基米德公理及穷竭法的使用).只是没有强大的生产需求和适宜的社会环境,未能进一步发展起来.
这位独步千古的科学家,还具有崇高的爱国热忱,在祖国危亡的紧急关头,献出了自己的一切.他的爱国精神和爱科学的精神同样为万世所景仰.
教学目标分析:
1、了解阿基米德的主要数学成就。
2、理解平衡法,并将其灵活运用于对球体体积的计算。
3、激发学生的求知欲,培养严谨的学习态度,培养积极进取的精神
重难点分析:
重点:了解阿基米德的主要数学成就
难点:理解平衡法。
教学准备:多媒体课件
教学过程:
一、知识讲解:
(一)导入:
金冠——阿基米德原理的发现
叙拉古的海厄罗王的政治威望及权势日益提高,为了报答诸神的德泽,他决定建造一个华贵的神龛,内装一个纯金的王冠,作为谢恩的奉献物 金匠如期完成了任务,理应得到奖赏.这时有人告密说金匠偷去一部分金子,以等重的银子掺入.国王甚为愤怒,但又无法判断是否确有其事.便请素称多能的阿基米德来鉴定一下,他也一时想不出好办法来.正在苦闷之际,他到公共浴室去洗澡,当浸入装满水的浴盆去的时候,水漫溢到盆外,而身体顿觉减轻.于是豁然开朗,悟到不同质料的物体,虽然重量相同,但因体积不同,排去的水必不相等.根据这一道理,不仅可以判断王冠是否掺有杂质,而且知道偷去黄金的份量.这一发现非同小可,阿基米德高兴得跳了起来,赤身奔回家中准备实验,口中不断大呼“尤里卡!尤里卡!”(Eureka,意思是“我找到了”.)
这问题可解释如下:设王冠重W,其中金与银分别重W1,W2,而W=W1+W2分别取重为W与W1的纯金放入水中,设排去水的重各 的银放入水中,设排去水的重量各为F2与y,于是W∶W2=F2∶y,由此推得F(W1+W2)=F1W1+F2W2,即用实验可求出F,F1,F2,即可算出银与金之比值.如F=F1,说明没有掺银.实际情况是两者不等,从而揭穿了金匠的劣行.
经过仔细实验和反复思考,将经验上升为理论,他终于发现了流体静力学的基本原理——阿基米德原理
(二)新科教授
1、阿基米德简介
阿基米德(Archimedes) 公元前287年生于西西里岛(Sicilia,今属意大利)的叙拉古(Sracusa,—译锡拉库萨);公元前212年卒于叙拉古.
阿基米德早年曾在当时希腊的学术中心亚历山大跟随欧几里得的门徒学习,对欧几里得数学进一步的发展作出了一定的贡献.阿基米德也算是亚历山大学派的成员,他的许多学术成果就是通过和亚历山大的学者通信往来保存下来的.后人对阿基米德给以极高的评价说:任何一张列出有史以来三个最伟大的数学家的名单中,必定会包括阿基米德,另外两个通常是牛顿和高斯.不过以他们的丰功伟绩和所处的时代背景来对比,拿他们的影响当代和后世的深邃久远来比较,还应首推阿基米德.
2、主要著作
阿基米德留下的数学著作不下10种,多数为希腊文手稿,也有的是13世纪以后从希腊文译成拉丁文的手稿.著作的题例,深受欧几里得《几何原本》的影响,先设立若干定义和假设,再依次证明各个命题.各篇独立成章,虽然不象《原本》那样浑然一体,但所言均有根据,论证也是严格的.现按海伯格本的顺序(为希思本所沿用)列举如下:
《论球与圆柱》《圆的度量》《劈锥曲面与回转椭圆体》《论螺线》《平面图形的平衡或其重心》 《数沙器》 《抛物线图形求积法》 《论浮体》 《引理集》《群牛问题》
在本世纪初还发现阿基米德的一封信,这信非常重要,它记录了阿基米德研究问题的独特思考方法,后来以《阿基米德方法》(The method of Archimedes,简称《方法》)的标题发表出来.
《方法》包括15个命题.一开头是写给埃拉托塞尼的信用来说明本篇的主要内容,相当于序言.下面,以命题1为例,阐明阿基米德的思想方法.为了便于了解,暂用现代的术语和符号来推导.
设D是抛物线弧ABC的弦AC的中点,过D作直线平行于抛物线的轴OY,交抛物线于B.要证明的是抛物弓形ABCD的面积等于△ABC面积的 4/3.当时已经知道过B的切线平行于AC,即B是弓形的顶点(在ABC弧上与AC距离最远的点).命题结论的另一种说法是: 抛物弓形的面积,是等底等高的三角形的4/3.用解析几何来分析,设抛物线方程是
y=ax2 (1)
A,C的横坐标分别是x1,x2,则AC的方程是 y=ax1x+ax2x-ax1x2 (2)
过C点的切线CF的方程是
延长DB交CF于E,不难证明,B是ED的中点.事实上,将D,B,
坐标,依次是
由此知B是D、E中点.
作AF‖OY,交CF于F.延长CB交AF于K,则K是FA的中点.再取KH=KC,过AC上任意点M作MQ‖OY,交CK于P,交CF于Q,交抛物线于N.将M的横坐标x2分别代入(2)、(1)、(3)得到M,N,Q的纵坐标
ym=ax1x0+ax2x0-ax1x2,
于是有:
3、各篇著作的主要内容
(1)《论球与圆柱》
例第5个公理,这就是后来以阿基米德的名字命名的公理:如果两条线段或两个面、两个立体不相等,就可以在两者之差的上面,加上它的本身,一次一次加上去,使得每一个预先给定的同类量都被超过.在现代分析学中常用的说法是:对于任意二正实数 a,b,必存在自然数n,使得na>b.
从这些定义和公理出发,推导出上卷44个,下卷9个命题.多次使用阿基米德公理及反证法(归谬法),如要证A=B,则证明A>B及A<B均导致矛盾.以下面的命题为例来说明.
阿基米德引用了欧几里得《几何原本》Ⅻ,2的证法(穷竭法)建立了命题6:只要边数足够多,圆外切正多边形的面积C与内接正多边形的面积1之差可以任意小.不同之处是欧几里得默认了阿基米德公理,而阿基米德在本篇中是明确地作为公理提出来的.在这基础上,证明了: 命题14.正圆锥体的侧面积等于以底面半径与母线的比例中项为半径的圆的面积.
设正圆锥的底面为A,半径为r,母线为l,r与l的比例中项为 R(即R2=rl),则此正圆锥的侧面积S=πR2.
以R为半径作圆B,其面积为πR2,现要证明S=B=πR2.用反证法,设S>B.根据命题6,可作B的外切正多边形Cn(同时表示其面积,下同)与内接正边形In,使得
又作底面A的相同边数的外切正多边形Dn,其周长记作Pn.以Dn为底,
Dn,Cn是相似的,其比等于对应线段平方之比,
由此知Cn=Ln,代入上面的不等式有
这是不合理的,因为圆锥侧面积S小于其外切棱锥侧面积Ln,而圆B大于其内接多边形面积In.同理可证S<B也是不合理的,故S=B=πR2.现在常用的形式是S=πrl.
下面较著名的命题还有命题33.球面积等于它的大圆面积的4倍.
命题34.球体积等于以它的大圆为底、它的半径为高的圆锥体积的4倍.推论:以球的大圆为底、球直径为高的圆柱的体积与表面积分别是球的体积与表面积的3/2.这命题在《方法》中已提出,此处用反证法加以证明.
命题35—44研究了球缺、球冠及球心角体(球扇形)的表面积及体积.
下卷9个命题主要讨论球缺,好几个是作图题.命题2给出球缺的体积.命题4在历史上占有特殊的地位.它要求用平面将一个球截成两部分,使这两部分体积之比等于给定的比.
设球半径为r,所分成的两个球缺的高各为h及2r-h,公共底的半
可改写为
记x=2r-h,a=3r,又将右端的常数写成bc2,上式简写成x2(a-x)=bc2.
此问题的解相当于用几何方法去解这个3次方程.阿基米德说他将在后面给出分析与综合的解法,但现存本未见,大概已失传.后来欧托基奥斯(5世纪时)找到一些残页,是用多利安方言(阿基米德惯用的方言)写的手稿,上有这问题的解法,他认为是属于阿基米德的.解法的要点是求两条圆锥曲线的交点.一条是抛物线
另一条是双曲线(a-x)y=ab.残页还讨论了方程可解的条件,这
时,还比较了狄俄尼索多罗(Dionysodo-rus,公元前3世纪—公元前2世纪,居住在小亚细亚地区)以及狄俄克利斯(Diocles,约公元前190年)对此问题的解法.
(二)《圆的度量》,其中只有3个命题.
命题1.圆的面积等于一个以其周长及半径作两个直角边的直角三角形的面积.
更简单的说法是:圆面积等于半径乘半周长.这正是中国《九章算术》的说法:“半周长半径相乘得积步”.或刘徽(公元263年)注的说法:“半周乘半径为圆幂”.
但在古希腊,自从毕达哥拉斯学派发现不可公度量以后,每一条线段是否都有长度就成了问题.因此在几何学家的著作中,极力避免两条线段长相乘的说法,宁愿说成由两线段构成的矩形或三角形的面积.
证明仍用穷竭法.圆半径为r,周长为C,面积为S.以C,r为两直角边作直角三角形,设面积为K.现证明S=K.用反证法,假定S>K,作边数足够多的内接正多边形In,使其面积In与圆面积S之差
S-In<S-K,
于是有
In>K.
这是不合理的,因为In的边心距d<r,而In的周长小于C,故In应<K.同理作外切正多边形,可证S<K也导致矛盾,从而有S=K.
命题2.圆面积与外切正方形面积之比为11∶14.
命题应该放在命题3的后面,也许是后人抄错了或阿基米德别有用意.
这就是有名的阿基米德圆周率的出处.欧几里得在《原本》中讨论了很多圆的性质,但却完全没有提到圆周率的值及圆面积、圆周长的计算法.阿基米德弥补了这一不足,并在科学上首次创用上、下界来确定一个量的近似值,还提供了误差的估计。
他在推导中使用了一个不等式
分数的渐近分数.它具有这样的特性,以265/153为例,在一切分母
的性质.阿基米德是怎样得到这些分数的?这引起后人的极大兴趣.仅从17世纪以来,就至少有十几种不同的推测.较多的意见认为是利用了不等式
左右各平方,便可证其成立.试推演如下:
取右端
于是有
本命题主要的推导思想如下:设O是圆心,OA是半径,作
∠AOB=30°,
过A作切线AB交OB于B.则
两式左右相加得
作∠AOB的平分线OC,则
左端分母与右端分子交换,再由前面的不等式,有
或
由上面的不等式立刻推出圆外切正6边形、正12边形的周长与直径比值的上界.同样,计算内接正多边形的边长,可以确定比值的下界.再利用比例关系及勾股定理,重复上述手续,一直算到96边形,最后得到
一切分母不大于71的分数中它是最接近π的.比它更接近π的分数有
①①见梁宗巨,祖冲之密率的优越性,《辽宁师范大学学报》增刊(数学史专辑),1986,p.6.
分母都大于71,除了最后一个外,都不是连分数的渐近分数.
(三)《劈锥曲面与回转椭圆体》
共32个命题,研究椭圆的面积以及回转圆锥曲线体被平面截取部分的体积等.证明的方法是穷竭法,十分接近今天的积分法思想.当时还没有“抛物线”(parabola)等名称,早期的希腊数学家如门奈赫莫斯(Menaechmus,公元前4世纪),用平面去截三种不同的直圆锥面,产生三种圆锥曲线.令平面与直圆锥的母线垂直,当圆锥的顶角(母线所张的最大角度)是直角时,截口叫做“直角圆锥截线”(section of a right-angled cone),现在叫抛物线;当顶角是锐角时,叫“锐角圆锥截线”(section of an acute-angledcone),现叫椭圆;当顶角是钝角时,叫“钝角圆锥截线”(section ofan obtuse-angled cone),现叫双曲线.欧几里得和阿基米德一直沿用这些旧名称,为简单起见,改用今名.
本篇一开头先给出两个引理,以备后面证明之用.第1个是等差数列求和公式,写成不等式
2(a+2a+3a+…+na)>n2a
>2[a+2a+3a+…+(n-1)a].
如用求和公式,左端是n(n+1)a,右端是(n-1)na,不等式成立是明显的.
第2个是自然数平方和公式,先证明
(n+1)(na)2+a(a+2a+3a+…+na)
=3[a2+(2a)2+(3a)2+…+(na)2],
由此可知
a2+(2a)2+(3a)2+…+(na)2
写成不等式
3Sn-1a2<n3a2<3Sna2.
下面以一个较简单的命题来阐明阿基米德的证题思想.为了便于理解,改用现代的术语和符号.
命题21.回转抛物体被垂直于轴的平面所截取的部分的体积等于同底等高的圆锥体的3/2.
抛物线AOB(不妨设方程为y=x2)绕其轴OC回转,产生回转抛物体.求被垂直于OC的平面ACB所截取的部分的体积V.将OC用分点O,C1,C2,…,Cn-1,Cn(=C)分成n等分,过这些分点作垂直于OC的平面将所求的体积分成n个小薄片.每一个小薄片介于一个内接圆柱与一个外接圆柱之间.例如E1H2及A1F2回转后就产生C1,C2间的小薄片的内接与外接圆柱.又每一个外接圆柱与紧接着上面的一个内接圆柱(如A0F1与E1H2回转产生的圆柱)相等.
=In.这是根据前面引理得出的不等式.现证明V=V*,否则,如V>V*,
Sn-In<V-V*,
这是不合理的,因Sn>V而In<V*.同理可证V<V*也导致矛盾,故
其余各命题虽然都比这复杂,但基本思路是差不多的.除了没有取极限这一步骤之外,基本思想和现代积分是一致的.
(四)《论螺线》
共28个命题,前10个是关于圆及切线的各种比例关系的.命题11重新证明了自然数平方和的不等式,这在《劈锥曲面与回转椭圆体》中是作为引理提出的:
接着给出螺线(现在称为“阿基米德螺线”)的定义.
一条射线绕其固定端点匀速旋转,同时有一动点从端点出发沿射线匀速运动,那么这动点就描绘出一条平面螺线(spiral).射线开始时的位置叫做始线(OA),固定端点叫做原点(O).旋转一圈所产生的螺线与始线所包围的面积叫做“第1面积”(first area).
现在在解析几何中螺线的极坐标方程是r=aθ,旋转一圈后动点到达A点,OA=2πa,以OA为半径的圆叫做“第1圆”.
命题21以后的几个命题探讨螺线所围的面积,命题24证明了“第1面积”S等于“第1圆”面积的1/3,即
螺线的内接与外接扇形.例如第3等分的内接扇形是ON2P3,外接扇形是OM2N3.设全部外接扇形面积的总和是Cn,内接扇形面积的总和是In,则Cn>S>In又根据自然数平方和的不等式,并注意到弓形面积公,有
可以任意小.
应用前面多次用过的反证法,可证S=S*.否则,如S>S*,则可使
Cn-In<S-S*,
这是不合理的,因外接扇形面积总和>S,而In<S*.同样S<S*也是不合理的.于是得到
命题13—20研究了螺线的切线,给出作图方法及种种性质.没有发现阿基米德有微分法的思想(那怕是粗浅的),那么他是怎样得到切线的作法的?这有趣而且带有关键性的问题引起后人的注意.有些学者认为是运用了运动学的原理.射线作匀角速运动,而动点在射线上作匀速运动,两个速度按平行四边形法则所得到的合速度方向就是切线方向.如果这推测正确的话,那么这就是古代属于微分法的罕见的例子.
(五)《平面图形的平衡或其重心》
分两卷,卷Ⅰ先给出7个公理,都是显而易见之理.例如1.等重的物体放在相等的距离上(各在杠杆一端,与支点等距),则处于平衡状态;等重的物体放在不相等的距离上则不平衡,向距离远的一端倾斜.
2.放在一定距离上的重物处于平衡状态时,若在其中的一个重物上加一点重量,则失去平衡,要向加重量的一端倾斜.
5.相似图形的重心,也处在相似的位置上.
从这些公理出发,导出了著名的杠杆定律:
命题6,7.若两重物平衡,则所处的距离(与支点的距离)与重量成反比.
证明是分可公度量与不可公度量两种情形来讨论的.下面的8个命题找出平行四边形、三角形以及梯形的重心.
卷2的10个命题集中研究了抛物弓形和它的一部分的重心.方法是作一系列的内接三角形,逐步去逼近所讨论的图形.
(六)《数沙器》
这是阿基米德遗留下来的唯一的算术著作,也可能是最后的一种.那时海厄罗王已去世(公元前216年),他的儿子吉伦(Gel-on)继承王位,阿基米德也已年逾古稀.这篇文章是递交给吉伦王的.
文章首先表明写作的目的,是要纠正有些人的错误观点,他们认为世界上的沙子是无穷的,即使不是无穷,也没有一个可以写出来的数超过沙子的数.阿基米德指出,任何大的数都可以表示出来.
全文只有一个定理,实际相当于现今的指数法则
Am·An=Am+n
他先给出地球、月球、太阳大小的估计,进而计算沙粒的数目.
1.地球的周长不大于3×106个“斯达地”(stadium,复数stadia).斯
的周长是5.55×105公里,而实际是40000公里.
2.地球直径大于月球直径,太阳直径大于地球直径.
3.太阳直径是月球直径的30倍.(实际是400倍)
这些估计数字和实际出入很大,不过他自己也说只是一种假定.接着推出
“宇宙”(相当于太阳系)直径<1010斯达地.
当时希腊用字母表示数字,最大的单位是“万”(10000,myri-ad),
表示加大10000倍.
阿基米德以万为基础,建立新的记数法,使得任何大的数都能表示出来.
从1起到1亿(原文是万万,myriad myriads,按中文的习惯改称为亿)叫做第1级(first order)数;以亿(108)为第2级数的单位,从亿(108)到亿亿(108)2叫第2级数;再以亿亿(108)2为单位,直到亿亿亿(108)3叫第3级数;照此类推,直到第1亿级数的最后一
原文全用语言来叙述,没有创设记数符号,他是否在别的地方使用了符号不得而知.为了叙述简明,这里用P表示亿亿(108)108.从1到P叫做第1周期(first period).下面列成表:
第1周期
第1级 从1到108
第2级 从108到(108)2
第2周期
第1级 从P到P·108
第2级 从P·108到P·(108)2
第108周期
+1位.
阿基米德算出充满宇宙的沙数不过是1051,即使扩充到“恒星宇宙”,即以太阳到恒星的距离为半径的大球,也只能容纳1063个沙粒,远远小于前面列出的大数.
现今从理论上推测,可观察到的宇宙半径约为130亿光年,假想整个充满了具有最小可能体积的粒子(如质子),其数也不超过10125.也还不能和上述的大数相比.
阿基米德的记数方法还可以继续下去,他企图说明任何大的数都可以表示出来,现在目的业已达到.可惜他没有再进一步去改革整个的希腊记数制度.也许那时已进行或临近叙拉古保卫战,致使改革工作功亏一篑.
(七)《抛物线图形求积法》
在《方法》中、阿基米德利用力学原理,已经得到“抛物弓形面积是同底等高的三角形的4/3”的结论.但他认为这不算证明,在本篇中另外用完全不同于力学的几何方法去严格证明它.基本思想是穷竭法,作一系列的内接三角形去穷竭(逼近)弓形,最后用归谬法完成证明.
全篇24个命题,最后一个命题才是所要的结论,前面的都可以看作是引理.为了避免叙述的冗长,下面用解析几何来说明.
设抛物线方程为
y2=2x
在抛物线上任取两点P1(x1,y1),P2(x2,y2),不妨设y1>y2.过P1P2中点M作MV‖抛物线的轴OX,交抛物线于V,V是抛物弓形P1VP2的顶点,即过V的切线‖于P1P2,ΔP1VP2与弓形同底等高(命题1与18已证).现要证明弓形面积S是ΔP1VP2面积的4/3.
过VP1中点M1作M1Q1‖OX交抛物线于Q1,过P2V中点M2作
称ΔP1VP2为1级三角形,面积记作Δ1,ΔP1Q1V及ΔP2VQ2称为2
VQ2,Q2P2之上作4个3级三角形,其面积总和为Δ3,同样可证
这手续可以继续下去,直到作出n级三角形,其面积的总和
由此知
又
前面的命题已证明,内接三角形的级数越多,In越大,S-In越小,同时Δn也越小,以至小于任给的正数.
或
这与前面的不等式矛盾.
In>S
这也是不合理的,因In是内接三角形面积之和,应有In<S.综上所述,
(八)《论浮体》
这是古代第一部流体静力学著作,阿基米德因此而被尊为流体静力学的创始人.20世纪之前,本书只有莫贝克13世纪时的拉丁文译本,1906年,海伯格发现了羊皮纸上的希腊原文,但不完全.现传的本子是两种文字参照编成的.
卷上命题7给出著名的“阿基米德原理”:重于流体的固体,放在流体中,所减轻的重量等于排去流体的重量.这原理因和他解决王冠问题联系起来而脍炙人口.
卷下的10个命题相当详细地讨论了正回旋抛物体在流体中的稳定性,研究了不同的高与底的比、具有不同的比重及在流体中处于不同位置时这种立体的性态.在推理中运用了高度的计算技巧.
(九)《引理集》
只有阿拉伯文译本传下来,是15个初等几何的问题集.也许不是阿基米德的原著而是后人收集整理的,因为在文章中不止一次提到阿基米德的名字.其中提出一种被称为“皮匠刀”(shoe-maker’s knife)的图形,是三个半圆所包围的部分,两个小半圆外切,又同时内切于大半圆.这图形有许多奇妙的性质,如通过两小圆的外切点C,作CP⊥大圆直径AB(三个圆的直径是重合的)交大圆于P,则“皮匠刀”AGCBPA的面积等于以CP为直径的圆面积.又可以作两个小圆,分别切于CP、大圆及一个小圆,可证这两个小圆相等.设HE是‖于AB的一个小圆的直径,则切点F与H,A共线,F与E,B也共线.E是ΔABD的垂心,从A向DB作垂线,垂足I必落在大圆周上.又AE,HC必过切点G,等等。还有许多其他的性质.
命题8和3等分角问题有关.设AB是⊙O的任一弦,延长AB至C使BC等于圆的半径.联CO并延长之使交圆于E,D.求证
联OA,OB,只要证明∠AOE=3∠BOD即可.实际上∠AOE=∠OAC+∠OCA=∠OBA+∠OCA=∠BOC+2∠OCA=3∠BOD.
现将问题倒过来考虑.设有∠AOE,求它的三等分角.这就是古希腊的三大作图问题之一的“三等分任意角”问题.从理论上说用直尺和圆规是不可能解决的.受到本命题的启发,只要在直尺上加一个点,就能轻而易举地解决这历史难题.
在直尺ABC上记上一个点B,使B至尺端C的距离等于半径.现令尺通过A点,B在圆周上移动,当C落在直径的延长线EDC上时,作ABC直线,则∠C就是所求的三等分角.
当然这已不是欧几里得几何的尺规作图法,因为工具已经改变(即使只加一点!),而且不合作图公法.不过它说明了一个问题,有些初学者只知道三等分角是难题,但不知难在尺规的限制上,如不限于尺规、那真是易如反掌.
(十)《群牛问题》
阿基米德的论文向来是以命题的形式来表达的,而这篇的体例不同,它是用诗句写成的(原文见[7],p.203).标题是给埃拉托塞尼的信.胡尔奇(Hultsch)曾猜想这是阿基米德“显本领”(tour de force)之作,以此向亚历山大的学者们(特别是阿波罗尼奥斯)挑战.但它的真实性颇值得怀疑,“群牛问题”大概很早以前就已存在,阿基米德只是重新研究而已.诗句也未必出自他的手.内容如下:
太阳神赫利俄斯(Helios)有一大群牛在西西里岛草原上放牧.公牛和母牛各有4种颜色,各种头数之间的关系如下:令W,w分别表示白色公牛、母牛的头数;
X,x……………黑色……………;
Y,y……………黄色……………;
Z,z……………花色…………….
要求
个三角形.倒数第2个条件是含混的,原话是“黑色和白色的公牛可以合起来排成一个方形,长与宽是相等的”.有两种可能解释,一是长与宽的数目相等,即
W+X=n2(完全平方数);
另一是方形的两个边长相等,但由于牛的身长与体宽不一样,方形两个边的数目并不相等,条件成为①①这种解释也很牵强,因为要挤成一个正方形,还需要考虑身长与体宽的比,故右端不是任意两个正整数之积mn而是kn2(k是常数),这样问题并没有化简.
W+X=mn.
后一种情形较易解决,称为“较简问题”,而前一种情形称为“完全问题”.
“较简问题”已由Jul.Fr.武尔姆(Wurm)解决.“完全问题”在1880年为阿姆托尔(Amthor)所解决.即使较简问题,牛的总数也已达到5916837175686头之多!而完全问题导致2元2次方程
t2-4729494u2=1.
最小解牛的总数是7 766×10206544,位数超过20万!当时阿基米德未必解得出来.
其他工作
(一)半正多面体(semi-regular polyhedron)
帕波斯在《数学汇编》中记述阿基米德发现了13种半正多面体.各个面是若干个不同类的正多边形,但同一类的都相等.例如12个相等的正5边形和80个相等的三角形构成一个92面体;6个正8边形,8个正6边形,12个正方形构成26面体;26面体又可以由18个正方形和8个正三角形构成.如此等等.
(二)三角形面积公式
阿拉伯数学家比鲁尼(Abū’l Raihān Muhammad al-Bīrūnī,973—1050?)记述,阿基米德发现了用边表三角形面积的公式
s是三角形三边a,b,c之和之半,这公式通常归功于海伦(He-ron,62年前后),并称为海伦公式.
(三)正7边形作图法
另一个阿拉伯数学家塔比伊本库拉(Thābit ibn Qurra,826—901)指出,阿基米德发现正7边形的作图法.自然不是尺规作图,可惜方法已失传,
(四)天文学方面
阿基米德对天文学也深有研究,但著作没有留下来.西塞罗的书记载马塞勒斯攻占叙拉古时,曾获得两座阿基米德制作的天文仪器.一座是天球仪,上刻各个星座,后放置在神庙中.另一座为加卢斯(Gain Sulpicius Gallus,公元前166年为罗马执政官)所有.可称为天象仪(planetarium),借助机械或水力表演日、月、行星的运行,还可以演示日、月食.
(五)阿基米德螺旋泵
历史学家狄奥多罗斯(Diodorus Siculus,公元前1世纪)记载阿基米德在埃及时,发明一种螺旋水泵,被埃及人广泛使用.
结束语
历史上有的数学家勇于开辟新的园地,而缺乏缜密的推理,有的数学家偏重于逻辑证明,而对新领域的开拓却徘徊不前.阿基米德则兼有二者之长,他将惊人的独创与严格的论证融为一体,更善于将计算技巧与逻辑分析结合起来.正确地注意理论与实际的联系,常常通过实践直观地洞察到事物的本质,然后运用逻辑方法使经验上升为理论(如浮力问题),再用理论去指导实际工作(如发明抗敌器械).在严格性方面,实超过了15—17世纪的分析学家,他的理论比牛顿、莱布尼茨更加接近柯西、外尔斯特拉斯的ε-δ方法(例如阿基米德公理及穷竭法的使用).只是没有强大的生产需求和适宜的社会环境,未能进一步发展起来.
这位独步千古的科学家,还具有崇高的爱国热忱,在祖国危亡的紧急关头,献出了自己的一切.他的爱国精神和爱科学的精神同样为万世所景仰.
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
