《周髀算经》与赵爽弦图 课件 (6)
文档属性
| 名称 | 《周髀算经》与赵爽弦图 课件 (6) |  | |
| 格式 | zip | ||
| 文件大小 | 909.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-06 18:57:49 | ||
图片预览


文档简介
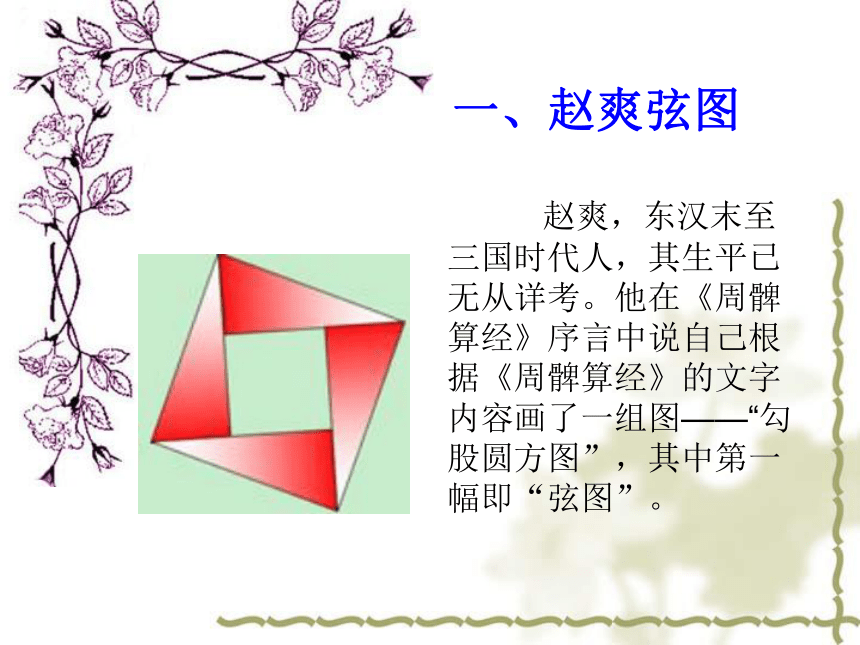
课件10张PPT。《周脾算经与赵爽弦图》一、赵爽弦图 赵爽,东汉末至三国时代人,其生平已无从详考。他在《周髀算经》序言中说自己根据《周髀算经》的文字内容画了一组图——“勾股圆方图”,其中第一幅即“弦图”。
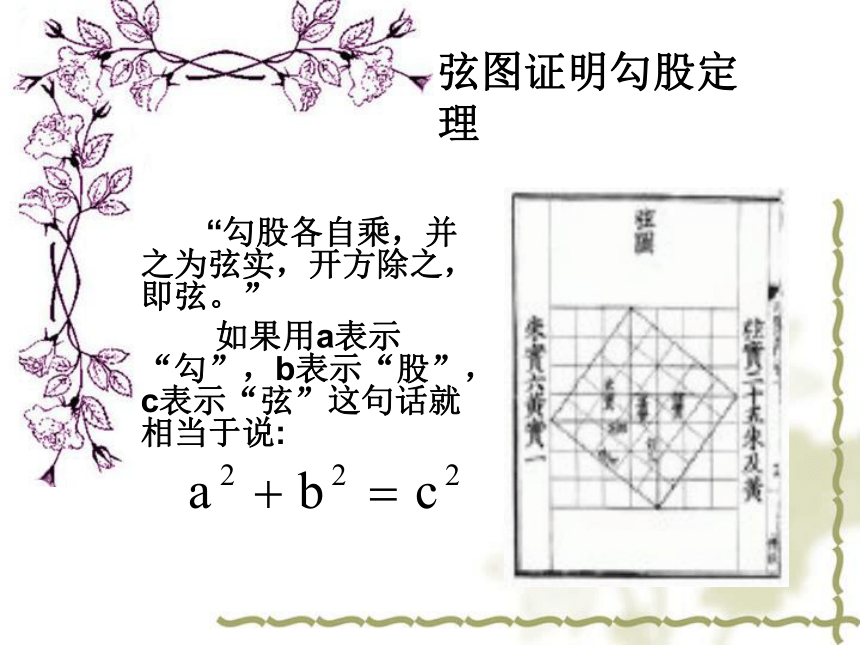
弦图证明勾股定理 “勾股各自乘,并之为弦实,开方除之,即弦。”
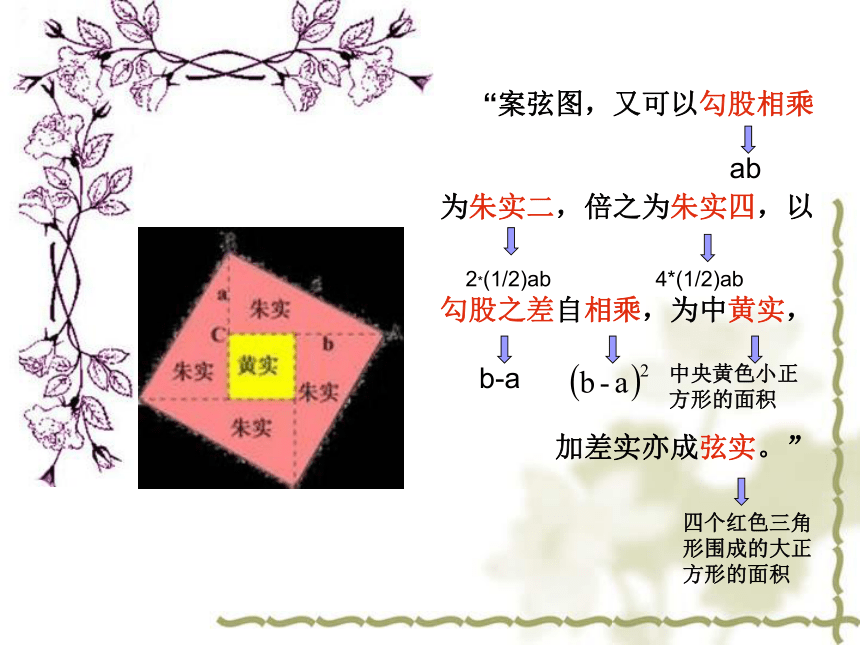
如果用a表示“勾”,b表示“股”,c表示“弦”这句话就相当于说:“案弦图,又可以勾股相乘 为朱实二,倍之为朱实四,以 勾股之差自相乘,为中黄实, 加差实亦成弦实。”b-a中央黄色小正方形的面积四个红色三角形围成的大正方形的面积ab商高答周公 周公问:没有梯子可供我们上天,又没有一把合适的尺子可供我们量地那么,怎样确定天有多高、地有多厚呢? 商高答:办法是有的,那就是利用勾、股、弦之间的关系,即勾三、股四、弦五。
又说:“既方之,外半其一矩,环而共盘,得成三、四、五。两矩共长二十有五,是为积矩。” 这段话引发了许多讨论,赵爽弦图给出的勾股定理的证明,很有可能是对商高这段文字的诠释。
根据《周髀算经》,影周公测日方法大致是这样的:先后两次测量同一圭表在不同处的日影长然后用公式:
日高=(表高×表距)/影长+表高
周
公
测
影
台勾股定理与量天测地二、出入相补原理 赵爽和刘徽作为证明勾股定理基础的出入相补原理——一个平面(立体)几何图形被分割成若干部分后,面积(体积)的综合保持不变。
事实上赵爽“勾股圆方图说”,可以说是一篇运用个出入相补原理的杰作,借助出入相补原理证明了数十条命题或公式,举例说,其中有一个已知长方形长宽之和及其面积求该长方形的长和宽的问题。假设长方形的宽和长分别为x、y。已知x+y=2c,面积xy=a2,即x(2c-x)=a2,根据图21,赵爽首先推出长宽差值平方为:
解得:
这相当于给出了二次方程:
的以公式:
表示两个根。
图21毕达哥拉斯三、勾股定理证明异趣 勾股定理可以说是人类最早发现、最基本的同时也是应用最广的一条数学定理。古代中国《周髀算经》中有关于勾股定理的记载。古埃及人没有留下这样明显的记录,但他们建造了蔚为奇观的金字塔。古巴比伦则不乏有关勾股定理的记载,巴比伦泥版文书中甚至出现有系列的“勾股数”,即 : a2+b2=c2 。
谢谢观赏!
弦图证明勾股定理 “勾股各自乘,并之为弦实,开方除之,即弦。”
如果用a表示“勾”,b表示“股”,c表示“弦”这句话就相当于说:“案弦图,又可以勾股相乘 为朱实二,倍之为朱实四,以 勾股之差自相乘,为中黄实, 加差实亦成弦实。”b-a中央黄色小正方形的面积四个红色三角形围成的大正方形的面积ab商高答周公 周公问:没有梯子可供我们上天,又没有一把合适的尺子可供我们量地那么,怎样确定天有多高、地有多厚呢? 商高答:办法是有的,那就是利用勾、股、弦之间的关系,即勾三、股四、弦五。
又说:“既方之,外半其一矩,环而共盘,得成三、四、五。两矩共长二十有五,是为积矩。” 这段话引发了许多讨论,赵爽弦图给出的勾股定理的证明,很有可能是对商高这段文字的诠释。
根据《周髀算经》,影周公测日方法大致是这样的:先后两次测量同一圭表在不同处的日影长然后用公式:
日高=(表高×表距)/影长+表高
周
公
测
影
台勾股定理与量天测地二、出入相补原理 赵爽和刘徽作为证明勾股定理基础的出入相补原理——一个平面(立体)几何图形被分割成若干部分后,面积(体积)的综合保持不变。
事实上赵爽“勾股圆方图说”,可以说是一篇运用个出入相补原理的杰作,借助出入相补原理证明了数十条命题或公式,举例说,其中有一个已知长方形长宽之和及其面积求该长方形的长和宽的问题。假设长方形的宽和长分别为x、y。已知x+y=2c,面积xy=a2,即x(2c-x)=a2,根据图21,赵爽首先推出长宽差值平方为:
解得:
这相当于给出了二次方程:
的以公式:
表示两个根。
图21毕达哥拉斯三、勾股定理证明异趣 勾股定理可以说是人类最早发现、最基本的同时也是应用最广的一条数学定理。古代中国《周髀算经》中有关于勾股定理的记载。古埃及人没有留下这样明显的记录,但他们建造了蔚为奇观的金字塔。古巴比伦则不乏有关勾股定理的记载,巴比伦泥版文书中甚至出现有系列的“勾股数”,即 : a2+b2=c2 。
谢谢观赏!
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
