大衍求一术 教案 (1)

大衍求一术
教学目标分析：
1、了解大衍求一术起源与主要内容。
2、培养学生主动学习的习惯，积极探索解决问题的良好习惯。
3、感受到大衍求一术的学术魅力，增强民族自豪感，激发学生努力学习数学的热情
重难点分析：
重点：了解大衍求一术的主要内容
难点：理解大衍求一术的解题方法。
教学准备：多媒体课件
教学过程：
（一）大衍求一术
中国古代算书《孙子算经》中有一著名的问题“物不知数”，原题为：今有物，不知其数。三、三数之，剩二；五、五数之剩三；七、七数之，剩二．问物几何？
这实际上是求解一次同余式组的问题。后来，南宋数学家秦九韶在其著作《数书九章》中对此类问题的解法作了系统的论述，并称之为大衍求一术。
大衍求一术内容：
设一次同余式组为
（1）
式中 都是整数。
如果 即两两互质。
并设
且
则组（1）的全部解为：
也就是说一次同余式（1）的解化归为解K个同余式的问题：
?????? 秦九韶称mi称为定母，V为衍母，Mi为衍数.xi为乘率。
也就是说，秦九韶的解法最后归结到解下面一种类型的同式问题。即A、B为互质的两整数，求出一整数,使满足同余式
其中A为定母，B为衍数，求出的称乘率。秦九韶把求乘率的方法称“大衍求一术”。
秦九韶先从B中屡减A ，使其余数G大衍求一术说：
“置寄右上，定居古下，天元一于左上。”
先立一图式：
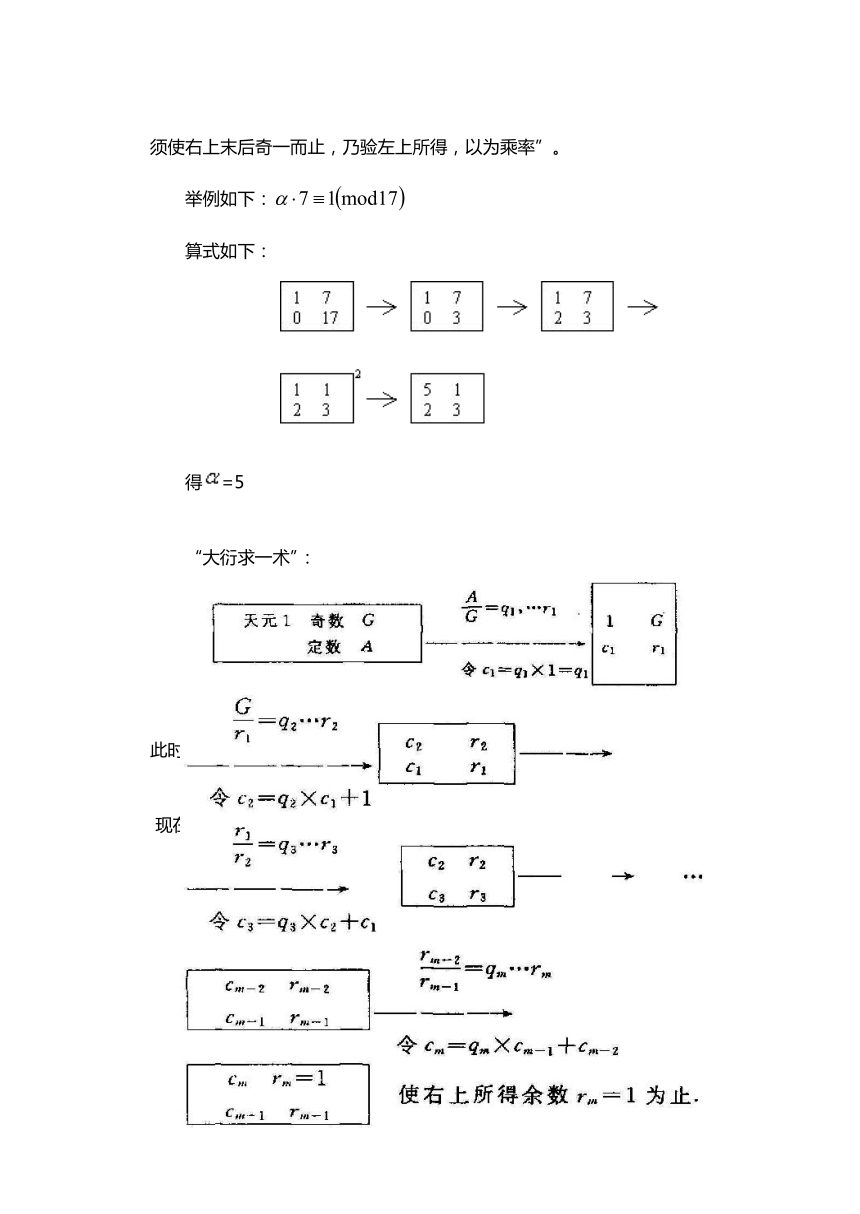
然后“先以右上除右下，所得商数与左上一相生，入左下，然后乃以后行上下，以少除多，递互除之，所得商数，随即递累乘，归左行上下，须使右上末后奇一而止，乃验左上所得，以为乘率”。
举例如下：
算式如下：
得=5
“大衍求一术”：
此时左上所得cm即为乘率，即=cm。
?现在证明=cm。由上计算变换式的箭头线上下得两组等式：
设，则由上两组等式可以推出：
当rm =1时，最后一等式为，
由此可知：
再根据 得
在各种计算问题中，所给的模数mi不 一定两两互素，且不可能都是整数。秦九韶把模数分为四种：1.元数：指一般整数；2.收数：指小数；3.通数；指分数；4.复数：指皆为10”的倍数。秦九韶把后三种先化为第一种，然后把不互素的化为互素。
（二）大衍求一术——中国剩余定理：
在欧洲，最早接触一次同余式的，是和秦九韶同时代的意大利数学家裴波那契，他在《算法之书》中给出了两个一次同余问题，但是没有一般的算法。这两个问题从形式到数据都和孙子物不知数题相仿，整个水平没有超过《孙子算经》。直到十八、十九世纪，大数学家欧拉于公元1743年、高斯于公元1801年对一般一次同余式进行了详细研究，才重新获得和秦九韶“大衍求一术”相同的定理，并且对模数两两互素的情形给出了严格证明。欧拉和高斯事先并不知道中国人的工作。公元1852年英国传教士伟烈亚力发表《中国科学摘记》，介绍了《孙子算经》物不知数题和秦九韶的解法，引起了欧洲学者的重视。
1876年，德国马蒂生首先指出孙子问题的解法和高斯方法一致，当时德国著名数学史家康托看到马蒂生的文章以后，高度评价了“大衍术”，并且称赞发现这一方法的中国数学家是“最幸运的天才”。
直到今天，“大衍求一术”仍然引起西方数学史家浓厚的研究兴趣。如1973年，美国出版的一部数学史专著《十三世纪的中国数学》中，在评论秦九韶的贡献时说道：“秦九韶在不定分析方面的著作时代颇早，考虑到这一点，我们就会看到，萨顿称秦九韶为‘他那个民族、他那个时代、并且确实也是所有时代最伟大的数学家之一’，是毫不夸张的。”
（三）“大衍求一术”命名：
在两种情形下（rn=1：n为偶数和n为奇数时），算法的最后一步都出现余数1，即“奇一而止”，整个计算到此终止，秦九韶因此把他的方法叫做“求一术”。
至于“大衍” 的意思，他在《数书九章》序中把它和《易经·系辞传》“大衍之数” 相附会：秦九韶认为这些问题与“卜筮”有关，“衍”同“演”，所以他在研究同余式解法后，便从《易经·系辞传》中的“大衍之数书五十，其用四十有九”摘取了“大衍”冠在算法上，称为“大衍求一术”。
（四）“大衍求一术”的应用：
大衍求一术是解决一次同于是问题的关键方法，在使用上很有价值，秦九韶举了很多需要用大衍求一术解决的应用问题，如“古利会积”、“积尺寻源”、“推记土功”、“程行计地”等等，广泛用于解决历法、工程、赋役和军旅等实际问题。
小结：从《孙子算经》“物不知数”题到秦九韶的“大衍求一术”，我国古代数学家对一次同余式的研究，不仅在中国数学史上而且在世界数学史上占有光荣地位。中国古代至迟从春秋战国时期就开始使用算筹记数，我们今天还可以从现存的公元前三世纪的货币上看到这种从左到右的记数方法。中国古代数学家对一次同余论的研究有明显的独创性和继承性，“大衍求一术”在世界数学史上的崇高地位是毋容置疑的，正因为这样，在西方数学史著作中，一直公正地称求解一次同余组的剩余定理为“中国剩余定理”。