中国古代数学家 课件 (3)

课件17张PPT。中国古代数学家1《九章算术注》公元263年撰《九章算术注》
阐述了中国传统数学的理论体系与数学原理
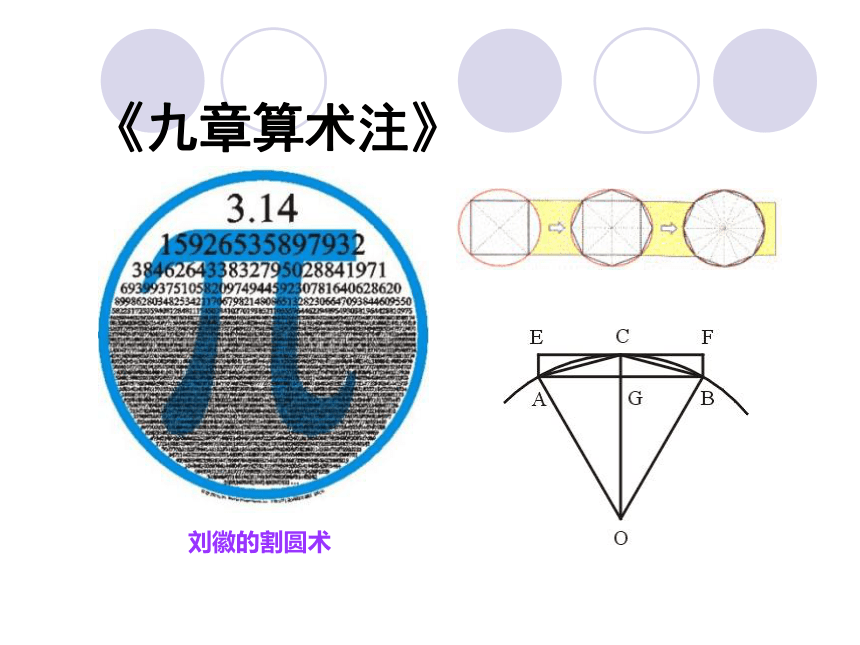
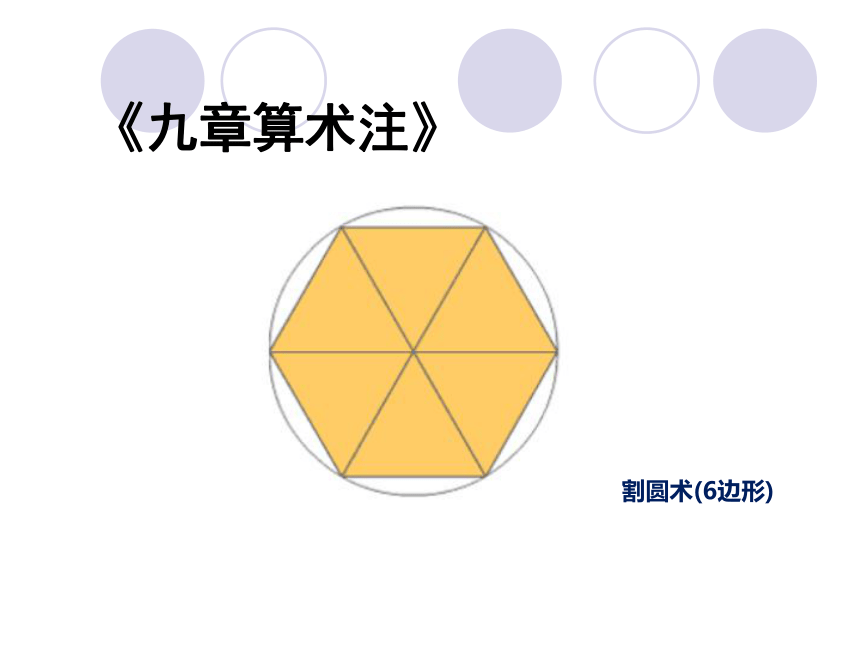
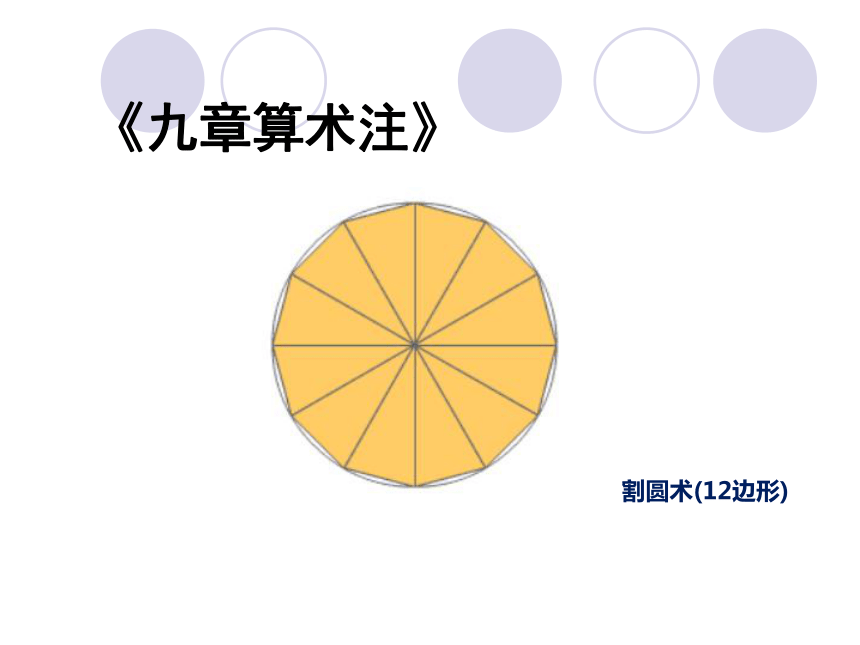
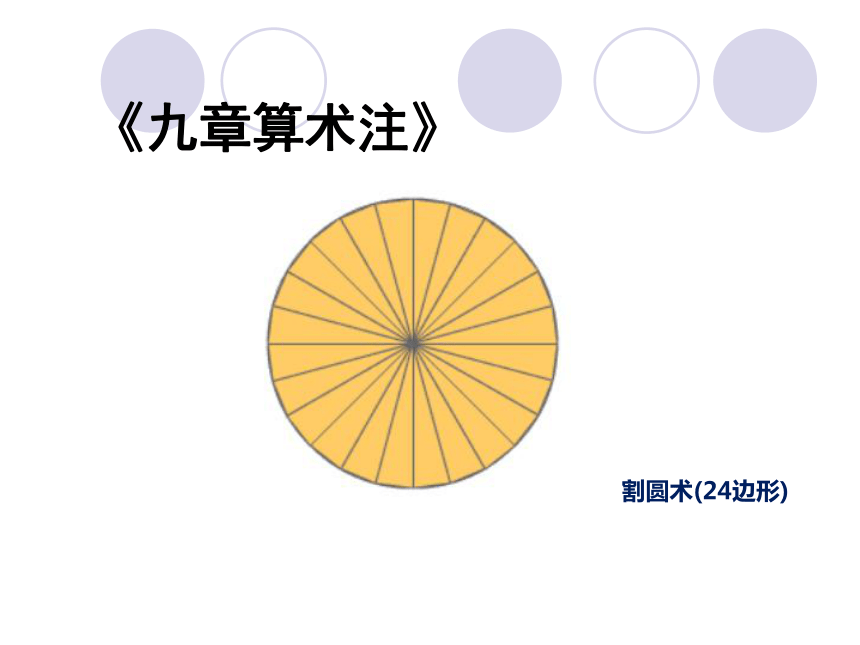
中国传统数学最具代表性的人物 刘徽(魏晋, 公元3世纪)（中国，2002）“徽幼习《九章》，长再详览。观阴阳之割裂，总算术之根源，探颐之暇，遂悟其意。是以敢竭顽鲁，采其所见，为之作注。”计算圆内接正3072边形求出圆周率为3927/1250 即3.1416 公元263年撰《九章算术注》。割圆术：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。” 刘徽的割圆术《九章算术注》徽率157/50即3.14 刘徽的割圆术 《九章算术注》割圆术(6边形)《九章算术注》割圆术(12边形)《九章算术注》割圆术(24边形)《九章算术注》割圆术(48边形)《九章算术注》割圆术(96边形)《九章算术注》刘徽对π的估算值（密克罗尼西亚，1999） 《九章算术注》《缀术》祖冲之(南朝宋、齐, 429-500) 圆周率计算 球体体积公式 古之九数，圆周率三，圆径率一，其术疏舛。自刘歆、张衡、刘徽、王蕃、皮延宗之徒，各设新率，未臻折衷。 宋末，南徐州从事史祖冲之，更开密法，以圆径一亿为一丈，圆周盈数三丈一尺四寸一分五厘九毫二秒七忽，朒数三丈一尺四寸一分五厘九毫二秒六忽，正数在盈朒二限之间。《缀术》《隋书》
（唐，魏征主编） 密率，圆径一百一十三，圆周三百五十五。约率，圆径七，周二十二。 1913年起称355/113为祖率。 所著之书,名为《缀术》,学官莫能究其深奥，是故废而不理。《缀术》《缀术》 圆内接正
12288边形和24576边形 割之又割 3.14159261<π<3.14159271《缀术》体积计算《缀术》祖氏原理 ：幂势既同则积不容异 卡瓦列里原理(1635)不可分量原理 卡瓦列里
(意, 1598-1647）小结刘微：
263年左右，六会发现当圆内接正多边形的变数无限增加时，多边形的面积则可无限逼近圆面积，即所谓“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周
合体而无所失矣。”刘徽采用了以直代曲、无限趋近、“内外夹逼”的思想，创立了“割圆术”祖冲之：
是我国杰出的数学家，科学家。南北朝时期人，汉族人，字文远。他当时就把圆周 率 精确到小数点后7位(3.1415926<圆周率<3.1415927)，比西方领先了1500年，并得出355/113的密率，22/7的约率。写书《缀术》，记载了他计算圆周率的方法，不过已经失传。
17