解析几何的进一步发展 课件 (1)
文档属性
| 名称 | 解析几何的进一步发展 课件 (1) |  | |
| 格式 | zip | ||
| 文件大小 | 994.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-06 20:53:53 | ||
图片预览









文档简介
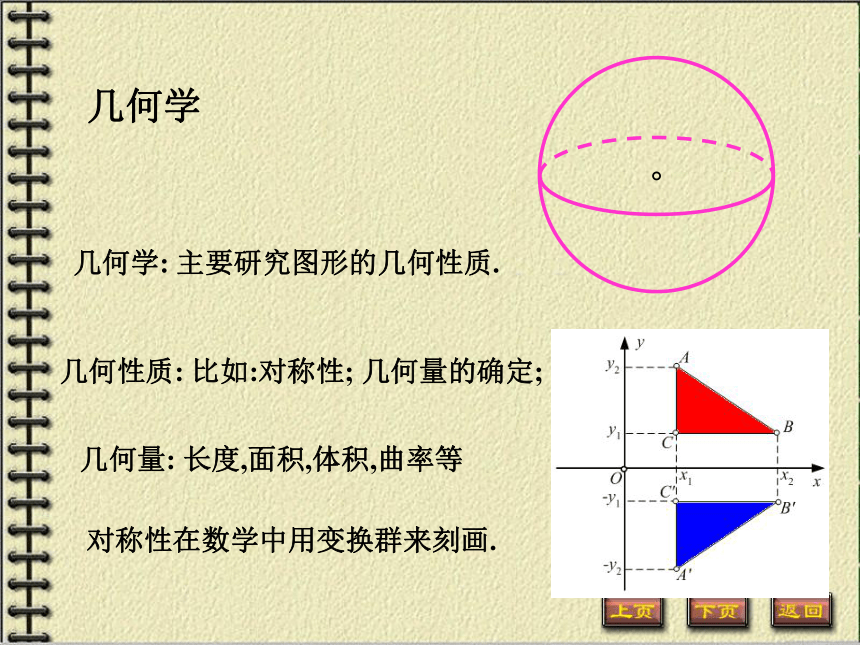
课件47张PPT。解析几何的进一步发展几何学几何学: 主要研究图形的几何性质.几何性质: 比如:对称性; 几何量的确定;对称性在数学中用变换群来刻画.几何量: 长度,面积,体积,曲率等解析几何:几何学方法论的学科.解析几何:代数方法.微分几何:用微分和积分的方法.保距变换群有限次平移、旋转、轴反射的复合的全体欧氏几何欧氏几何: 研究图形的保距变换不变性的科学欧氏几何仿射几何例如: 三维空间中两个图形怎样判断它们在仿射变换下全等?射影几何M?bius几何Laguerre几何Lie球几何Riemann几何Finsler几何解析几何的基本思想:
用代数的方法来研究几何.
解析几何的基本方法:
建立几何上的对象与代数对象之间的一一对应. 用代数的方法研究几何图形. 。(1)建立向量与几何对象(向量与有向线段)建立一一对应.
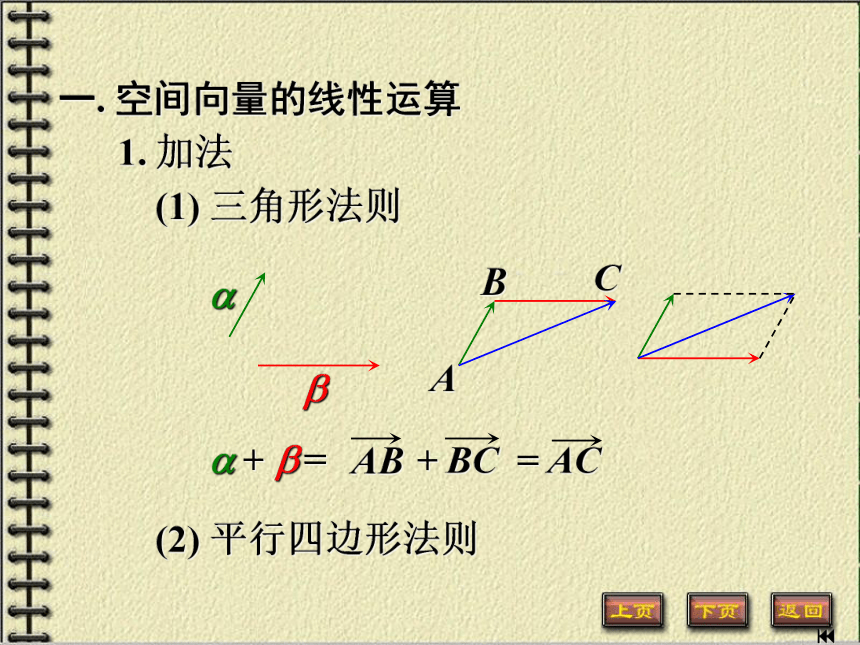
(2)建立坐标系,空间的几何对象(点)就可以用代数对象(有序数对)表示.定义. 既有大小又有方向的量叫做向量,或称矢量.向量(Vector)向量相等: 大小, 方向.注意向量相等与有向线段相等的差异.利用这种对应,直观定义两个向量的垂直(或正交),平行.规定:零向量与任何向量正交.所有的零向量都相等.长度为1的向量.零向量:单位向量: 定义 大小相等但方向相反的两个向量叫做互为反向量.一. 空间向量的线性运算 1. 加法 ? ? + ? = + (1) 三角形法则 注: ||?|| ? ||?|| ? ||? +? || ? ||?|| + ||? ||. 一. 空间向量的线性运算 1. 加法 ? (1) 三角形法则 (2) 平行四边形法则 ? + ? = + ? (3) 负向量 ?? (4) 向量的减法 ? ? ? = ? + (??). ? ?? ? (4) 运算性质 ① 交换律 ? + ? = ? + ? . ② 结合律 (? + ? ) + ? = ? + (? + ? ). ③ ? + ? = ?. ④ ? + (??) = ?. ?? ? ? 例1.C A B D G E F H ? 2. 数乘 ? ——向量 k ——数 k? ——向量 大小: |k|?||?|| 方向 k = 0或? = ?时: 无
k > 0且? ? ?时: 同?
k < 0且? ? ?时: 同?? ? = 2?, (1) 定义 ? ① 1? = ? ;
② (ab)? = a(b?);
③ (a+b)? = a? + b? ;
④ a(? +?) = a? + a? . (2) 运算性质 注: (?1)? = ?? .数乘 负向量 单位向量: 大小等于1的向量.规定:零向量与任何共线的向量组共线. 定义 平行于同一直线的一组向量叫做共线向量. 定义 平行于同一平面的一组向量叫做共面向量.规定:零向量与任何共面的向量组共面.? 4. 共线/共面问题 点O, A1, A2, …, As在同一直线上. ?1, ?2, …, ?s共线: 点O, A1, A2, …, As在同一平面上. ?1, ?2, …, ?s共面: ? 3. 线性组合 ?1, ?2, …, ?s ——向量 k1, k2, …, ks ——数 k1?1 + k2?2 + … + ks?s ——向量 ?1, ?2, …, ?s 的一个线性组合 ? ?k1, k2, …, ks使? = k1?1 + k2?2 + … + ks?s ?能由?1, ?2, …, ?s线性表示: ?不全为零的k1, k2, …, ks使?1, ?2, …, ?s线性相关: ?1, ?2, …, ?s , ? ——向量 k1?1 + k2?2 + … + ks?s = ? k1?1 +k2?2 + … +ks?s = ? ? k1=k2= … =ks= 0. ?1, ?2, …, ?s线性无关: ? (2) 判定 ? = 2?, 定理1. ? ? ?, 则 ?与?共线 ? ?能由?线性表示 且表示方式是唯一的. 推论. ?, ?共线 ? ?, ?线性相关. 2? ? ? = ?, 2? +? = ?. ? = k1? + k2? 定理2. ?与?不共线, 则 ?与?, ?共面 ? ? 能由?, ?线性表示 且表示方式是唯一的. 推论. ?, ?, ? 共面? ?, ?, ? 线性相关. ?k1? ? k2? + 1? = ? ? 定理3. ?, ?, ? 不共面, 则 任意向量δ ,可以由?, ?, ? 线性表出,
即存在数a,b,c, δ=a?+b?+c? .且表示方式是唯一的. ? 例2. 证明: A, B, C, D四点共面 ? 对任意点O存在不全为零的实数a, b, c, d 使得a + b + c + d = 0且 ? 证明: (?) A, B, C, D四点共面? 存在不全为零的实数a, b, c使得 令d = ? (a+b+c)即可. ? 证明: (?) 不妨设a ? 0. ? d = ? (a+b+c). a + b + c + d = 0aOA + bOB + cOC + dOD= ? = ? 证明: (?) 不妨设a ? 0. ? A, B, C, D四点共面. = ? ? DA, DB, DC共面 ? d = ? (a+b+c). a + b + c + d = 0? 例3. 证明: A, B, C三点共线 ? 对任意给定点O,存在实数 b, c使得 b + c = 1且 定义 设P1, P2为通常直线上的两个相异的点, P为该直线上任一通常点. 定义为P1, P2 , P的简单比, 或称单比. 称P1, P2为基点, P为分点.? 定理3. ?, ?, ? 不共面, 则 任意向量δ ,可以由?, ?, ? 线性表出,
即存在数a,b,c, δ=a?+b?+c? .且表示方式是唯一的. 一. 仿射坐标系 ? = ae1 + be2 + ce3 一. 仿射坐标系 ? 定义:空间中一点O与三个不共面向量 e1,e2,e3
一起构成空间的一个仿射标架,记[O, e1,e2,e3].
称e1,e2,e3为它的坐标向量. O称为它的原点.
对于空间任意一点A, 把向量OA(称为A的定位向量)对e1,e2,e3 的分解系数构成的有序数组称为A关于上述仿射标架的仿射坐标.? 对于仿射坐标系{O; e1, e2, e3}中的 任意点A, 存在唯一的有序数组 ? 对于仿射坐标系{O; e1, e2, e3}中的 任意向量?, 存在唯一的有序数组 (a, b, c)使得? = ae1 + be2 + ce3. (a, b, c)称为α?
关于仿射坐标系[O,e1 ,e2 ,e3 ]的坐标? 定理. 对于仿射坐标系{O; e1, e2, e3}中的 任意向量?, 存在唯一的有序数组 (a, b, c)使得? = ae1 + be2 + ce3. 坐标原点 点P的定位向量 坐标向量或基 ?的坐标 ? 右手仿射坐标系 O e2 e1 e3 左手仿射坐标系 ? 坐标轴 坐标平面 卦限 VI VII I II III IV V VIII 对于仿射坐标系{O; e1, e2, e3}中的坐标向量都是
单位向量且两两正交, 则称仿射坐标系{O; e1, e2, e3}为直角坐标系.同样的, 我们可以定义平面上的坐标系? (a, b, c) ——点P的(直角)坐标 y z x O ? P ? 二. 空间向量线性运算的坐标表示 ? + ? = (a1+b1, a2+b2, a3+b3), ? = (a1, a2, a3), ? = (b1, b2, b3), ? + ? = (a1+b1)e1+ (a2+b2) e2+ (a3+b3)e3, ? = a1e1+ a2 e2+ a3e3, ? = b1e1+ b2 e2+ b3e3, k? = ka1e1+ ka2 e2+ ka3e3, = (ka1, ka2, ka3). ? ? = (a1, a2, a3), ? = (b1, b2, b3), k? + l? = k(a1, a2, a3) + l(b1, b2, b3) = (ka1, ka2, ka3) + (lb1, lb2, lb3) = (ka1+lb1, ka2+lb2, ka3+lb3) ? 例4. P1(x1, y1, z1), P2(x2, y2, z2). = (x2, y2, z2) ? (x1, y1, z1) = (x2?x1, y2?y1, z2?z1). ? 例5. P1(x1, y1, z1), P2(x2, y2, z2),
(P1,P2,P)= ? (? ? ?1), 求P(x, y, z). xyzP1PO? ? P2? ???定理, 两非零向量
共线的充要条件是对应分量成比例,即:推论 三点
共线的充要条件是:定理 , 三非零向量
和 共面的充要条件是:推论 四个点
共面的充要条件是:或例. 已知向量a, b, c的分量如下: (1) a={0, -1, 2},b={0, 2, -4},c={1, 2, -1}; (2) a={1, 2, 3},b={2, -1, 0},c={0, 5, 6}. 试判别它们是否共面?能否将c表成a,b的线性组合?若能表示,写出表示式.
用代数的方法来研究几何.
解析几何的基本方法:
建立几何上的对象与代数对象之间的一一对应. 用代数的方法研究几何图形. 。(1)建立向量与几何对象(向量与有向线段)建立一一对应.
(2)建立坐标系,空间的几何对象(点)就可以用代数对象(有序数对)表示.定义. 既有大小又有方向的量叫做向量,或称矢量.向量(Vector)向量相等: 大小, 方向.注意向量相等与有向线段相等的差异.利用这种对应,直观定义两个向量的垂直(或正交),平行.规定:零向量与任何向量正交.所有的零向量都相等.长度为1的向量.零向量:单位向量: 定义 大小相等但方向相反的两个向量叫做互为反向量.一. 空间向量的线性运算 1. 加法 ? ? + ? = + (1) 三角形法则 注: ||?|| ? ||?|| ? ||? +? || ? ||?|| + ||? ||. 一. 空间向量的线性运算 1. 加法 ? (1) 三角形法则 (2) 平行四边形法则 ? + ? = + ? (3) 负向量 ?? (4) 向量的减法 ? ? ? = ? + (??). ? ?? ? (4) 运算性质 ① 交换律 ? + ? = ? + ? . ② 结合律 (? + ? ) + ? = ? + (? + ? ). ③ ? + ? = ?. ④ ? + (??) = ?. ?? ? ? 例1.C A B D G E F H ? 2. 数乘 ? ——向量 k ——数 k? ——向量 大小: |k|?||?|| 方向 k = 0或? = ?时: 无
k > 0且? ? ?时: 同?
k < 0且? ? ?时: 同?? ? = 2?, (1) 定义 ? ① 1? = ? ;
② (ab)? = a(b?);
③ (a+b)? = a? + b? ;
④ a(? +?) = a? + a? . (2) 运算性质 注: (?1)? = ?? .数乘 负向量 单位向量: 大小等于1的向量.规定:零向量与任何共线的向量组共线. 定义 平行于同一直线的一组向量叫做共线向量. 定义 平行于同一平面的一组向量叫做共面向量.规定:零向量与任何共面的向量组共面.? 4. 共线/共面问题 点O, A1, A2, …, As在同一直线上. ?1, ?2, …, ?s共线: 点O, A1, A2, …, As在同一平面上. ?1, ?2, …, ?s共面: ? 3. 线性组合 ?1, ?2, …, ?s ——向量 k1, k2, …, ks ——数 k1?1 + k2?2 + … + ks?s ——向量 ?1, ?2, …, ?s 的一个线性组合 ? ?k1, k2, …, ks使? = k1?1 + k2?2 + … + ks?s ?能由?1, ?2, …, ?s线性表示: ?不全为零的k1, k2, …, ks使?1, ?2, …, ?s线性相关: ?1, ?2, …, ?s , ? ——向量 k1?1 + k2?2 + … + ks?s = ? k1?1 +k2?2 + … +ks?s = ? ? k1=k2= … =ks= 0. ?1, ?2, …, ?s线性无关: ? (2) 判定 ? = 2?, 定理1. ? ? ?, 则 ?与?共线 ? ?能由?线性表示 且表示方式是唯一的. 推论. ?, ?共线 ? ?, ?线性相关. 2? ? ? = ?, 2? +? = ?. ? = k1? + k2? 定理2. ?与?不共线, 则 ?与?, ?共面 ? ? 能由?, ?线性表示 且表示方式是唯一的. 推论. ?, ?, ? 共面? ?, ?, ? 线性相关. ?k1? ? k2? + 1? = ? ? 定理3. ?, ?, ? 不共面, 则 任意向量δ ,可以由?, ?, ? 线性表出,
即存在数a,b,c, δ=a?+b?+c? .且表示方式是唯一的. ? 例2. 证明: A, B, C, D四点共面 ? 对任意点O存在不全为零的实数a, b, c, d 使得a + b + c + d = 0且 ? 证明: (?) A, B, C, D四点共面? 存在不全为零的实数a, b, c使得 令d = ? (a+b+c)即可. ? 证明: (?) 不妨设a ? 0. ? d = ? (a+b+c). a + b + c + d = 0aOA + bOB + cOC + dOD= ? = ? 证明: (?) 不妨设a ? 0. ? A, B, C, D四点共面. = ? ? DA, DB, DC共面 ? d = ? (a+b+c). a + b + c + d = 0? 例3. 证明: A, B, C三点共线 ? 对任意给定点O,存在实数 b, c使得 b + c = 1且 定义 设P1, P2为通常直线上的两个相异的点, P为该直线上任一通常点. 定义为P1, P2 , P的简单比, 或称单比. 称P1, P2为基点, P为分点.? 定理3. ?, ?, ? 不共面, 则 任意向量δ ,可以由?, ?, ? 线性表出,
即存在数a,b,c, δ=a?+b?+c? .且表示方式是唯一的. 一. 仿射坐标系 ? = ae1 + be2 + ce3 一. 仿射坐标系 ? 定义:空间中一点O与三个不共面向量 e1,e2,e3
一起构成空间的一个仿射标架,记[O, e1,e2,e3].
称e1,e2,e3为它的坐标向量. O称为它的原点.
对于空间任意一点A, 把向量OA(称为A的定位向量)对e1,e2,e3 的分解系数构成的有序数组称为A关于上述仿射标架的仿射坐标.? 对于仿射坐标系{O; e1, e2, e3}中的 任意点A, 存在唯一的有序数组 ? 对于仿射坐标系{O; e1, e2, e3}中的 任意向量?, 存在唯一的有序数组 (a, b, c)使得? = ae1 + be2 + ce3. (a, b, c)称为α?
关于仿射坐标系[O,e1 ,e2 ,e3 ]的坐标? 定理. 对于仿射坐标系{O; e1, e2, e3}中的 任意向量?, 存在唯一的有序数组 (a, b, c)使得? = ae1 + be2 + ce3. 坐标原点 点P的定位向量 坐标向量或基 ?的坐标 ? 右手仿射坐标系 O e2 e1 e3 左手仿射坐标系 ? 坐标轴 坐标平面 卦限 VI VII I II III IV V VIII 对于仿射坐标系{O; e1, e2, e3}中的坐标向量都是
单位向量且两两正交, 则称仿射坐标系{O; e1, e2, e3}为直角坐标系.同样的, 我们可以定义平面上的坐标系? (a, b, c) ——点P的(直角)坐标 y z x O ? P ? 二. 空间向量线性运算的坐标表示 ? + ? = (a1+b1, a2+b2, a3+b3), ? = (a1, a2, a3), ? = (b1, b2, b3), ? + ? = (a1+b1)e1+ (a2+b2) e2+ (a3+b3)e3, ? = a1e1+ a2 e2+ a3e3, ? = b1e1+ b2 e2+ b3e3, k? = ka1e1+ ka2 e2+ ka3e3, = (ka1, ka2, ka3). ? ? = (a1, a2, a3), ? = (b1, b2, b3), k? + l? = k(a1, a2, a3) + l(b1, b2, b3) = (ka1, ka2, ka3) + (lb1, lb2, lb3) = (ka1+lb1, ka2+lb2, ka3+lb3) ? 例4. P1(x1, y1, z1), P2(x2, y2, z2). = (x2, y2, z2) ? (x1, y1, z1) = (x2?x1, y2?y1, z2?z1). ? 例5. P1(x1, y1, z1), P2(x2, y2, z2),
(P1,P2,P)= ? (? ? ?1), 求P(x, y, z). xyzP1PO? ? P2? ???定理, 两非零向量
共线的充要条件是对应分量成比例,即:推论 三点
共线的充要条件是:定理 , 三非零向量
和 共面的充要条件是:推论 四个点
共面的充要条件是:或例. 已知向量a, b, c的分量如下: (1) a={0, -1, 2},b={0, 2, -4},c={1, 2, -1}; (2) a={1, 2, 3},b={2, -1, 0},c={0, 5, 6}. 试判别它们是否共面?能否将c表成a,b的线性组合?若能表示,写出表示式.
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
