平面解析几何的产生 课件 (2)

课件17张PPT。平面解析几何的产生 1、平面解析几何产生的背景
2、平面解析几何产生的历史
3、平面解析几何的基本思想
4、平面解析几何的发展
5、数形结合的思想
6、平面解析几何的产生与数形结合的思想的联系与地位
1、平面解析几何产生的背景
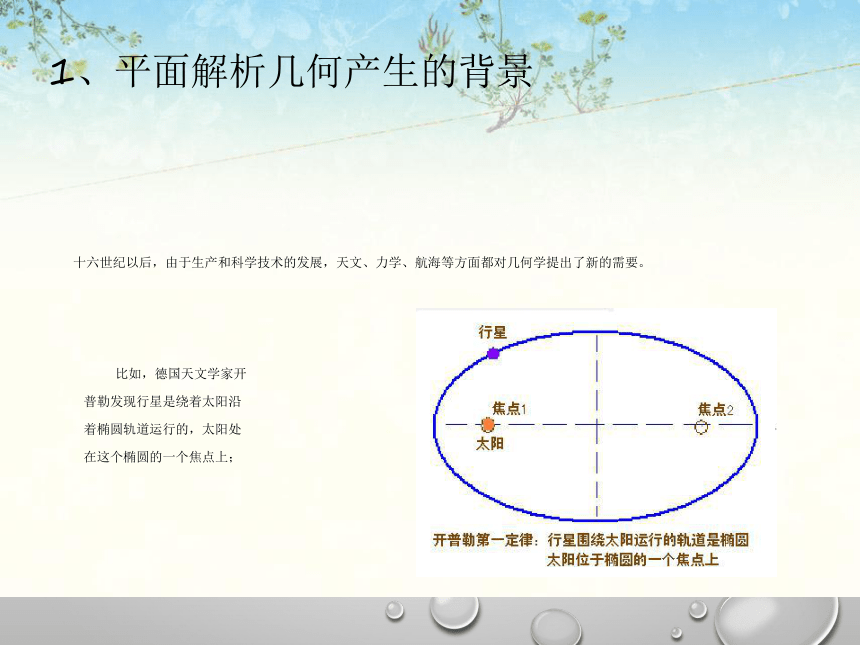
十六世纪以后，由于生产和科学技术的发展，天文、力学、航海等方面都对几何学提出了新的需要。

比如，德国天文学家开
普勒发现行星是绕着太阳沿
着椭圆轨道运行的，太阳处
在这个椭圆的一个焦点上；

意大利科学家伽利略发现投掷物体是沿着抛物线运动的。

这些发现都涉及到圆锥曲线，要研究这些比较复杂的曲线，原先的一套方法显然已经不适应了，这就导致了解析几何的出现。2、平面解析几何产生的历史
笛卡尔
1637年，法国的哲学家和数学家笛卡尔
发表了他的著作《方法论》，这本书的
后面有三篇附录，一篇叫《折光学》，
一篇叫《流星学》，一篇叫《几何学》。
笛卡尔的中心思想是建立起一种
“普遍”的数学，把算术、代数、
几何统一起来。
费尔玛
虽是一位业余数学家，在
牛顿、莱布尼兹大体完成微
积分之前，他是为创立微积
分作出贡献最多的人．
对数论、解析几何、概率
论三个方面都有重要贡献。
3、平面解析几何的基本思想 笛卡尔从天文和地理的经纬制度出发，指出平面上的点和实
数对(x,y)的对应关系。x,y的不同数值可以确定平面上许多不同的
点，这样就可以用代数的方法研究曲线的性质。这就是解析几何
的基本思想。

　 具体地说，平面解析几何的基本思想有两个要点：第一，在
平面建立坐标系，一点的坐标与一组有序的实数对相对应；第二，
在平面上建立了坐标系后，平面上的一条曲线就可由带两个变数
的一个代数方程来表示了。
4、平面解析几何的发展
欧几里得几何
非欧几何
坐标几何
群的概念
几何局部化
几何整体化欧几里得几何欧几里得在公元前300年左右写了《几何原本》。
它的主要结论有两个:
　(1)毕达哥拉斯定理 这条定理就是我们常说的勾股定理:设有一直角三角形，则长边的平方等于其它两边的平方和。
　(2)三角形三内角之和等于180° 如果以弧度为单位，也可以说三角形三内角之和等于π。
非欧几何从三角形三内角之和等于180°这个结论，而有接下来的重要发展:
(1) 球面几何 我们所讨论的三角形，并不一定都要在平面上，也可以是一个球面三角形，在这种情形下，三角形三内角之和必然大于180°，并且有一个非常重要的公式:
　　　　　A+B+C-π= S/R2
(2) 双曲型的非欧几何 在这种情形下，三角形三内角之和是小于180°的，即有如下的重要公式:
　　　　A+B+C-π= -S/R2
在空间或者“平面”的曲率，可以是正的，像球面几何；也可以是负的，像双曲几何。而其相对应的三角形三内角和，也分别有大于或小于180°的情形，不再满足欧几里得的平行公理，因此它们也被称作“非欧几何”。
坐标几何欧几里得几何之后，还有一个重要的发展是坐标几何。
有了解析几何，即可用解析的方法进行几何学的讨论。
　　 这样的发展不但使几何问题的处理容易些，而且更有其重大的意义:
　(1)解析化之后，可扩大所研究的图形的范围。
　(2)研究的图形不再局限在二维的平面上，而可推广至高维空间。
群的概念 群的概念，这是数学上一个基本的结构。数学总是要运算，加、减、乘、除。
要把一个物体从甲地移到乙地，再移到丙地，亦可直接把物体从甲地移到丙地，即两个运动的结果，可经由一次运动来达成；具有这个特殊性质的，便称为一个群，几何学研究的对象，应是经运动群变换后不变的几何性质。
研究几何性质在投影群变换之下不变的是投影几何。
在几何学的发展之中，有许许多多不同的几何学，像欧几里得几何学、投影几何学……及其他种种几何学，自然就要有一个人把它综合集结起来，他就是德国的数学家克莱因。
克莱因把几何学建立在群的观念上:一个空间有一个变换群，允许把空间的图形从这个位置移到另一个位置；因此有了一个群之后，便有一种几何，研究经过这个变换群变换之后保持不变的所有图形的几何性质。
几何局部化黎曼所创立的几何把几何局部化，可以说是几何学的第四个发展，这是笛卡尔坐标几何的自然推广。
1854年，黎曼在为取得大学教授资格的公开演讲上，发表了关于黎曼几何的第一篇论文。
真正使黎曼几何受到重视的是爱因斯坦的广义相对论。
几何整体化 黎曼几何把几何局部化，但我们不能永远只在一个小区域里面，所以局部化之后又要整体化，又要把它扩充到全空间。几何整体化可说是几何学的第五个发展。而在这个整体化的扩充中，最要紧的就是拓扑学，即俞大维先生说的“橡皮几何学”。

大家觉得微分几何应该是很有用的，因为在物理学发展之中，电磁学对人类日常生活是最有影响的；而在遗传工程及其他方面，DNA 的结构也是生物科学对人类生活最有影响的一门学问。而微分几何就是研究这两门学问的数学基础。
谢谢观赏！