二次函数的图像和性质同步练习(无答案)
文档属性
| 名称 | 二次函数的图像和性质同步练习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 214.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-07 14:46:13 | ||
图片预览

文档简介
二次函数图像和性质专题训练
1、将二次函数y=x2+2x﹣1的图象沿x轴向右平移2个单位长度,得到的函数表达式是( )
A.y=(x+3)2﹣2 B.y=(x+3)2+2 C.y=(x﹣1)2+2 D.y=(x﹣1)2﹣221·cn·jy·com
2、已知关于x的方程只有一个实数根,则实数a的取值范围是( )
A.a>0 B.a<0 C.a≠0 D.a为一切实数
3、若(2,5),(4,5)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是( )
A.x=1 B.x=2 C.x=3 D.x=4
4、关于二次函数y=﹣2x2+1的图象,下列说法中,正确的是( )
A.对称轴为直线x=1 B.顶点坐标为(﹣2,1)
C.可以由二次函数y=﹣2x2的图象向左平移1个单位得到
D.在y轴的左侧,图象上升,在y轴的右侧,图象下降
5、下列函数中:①y=﹣3x;②y=2x﹣1;③;④y=﹣x2+2x+3(x>2),y的值随着x的增大而增大的函数个数有( )www.21-cn-jy.com
A.4个 B.3个 C.2个 D.1个
6、在平面直角坐标系x′O′y′中,如果抛物线y′=2x′2不动,而把x轴、y轴分别向下、向左平移2个单位,则在新坐标系下抛物线的表达式为( )【来源:21·世纪·教育·网】
A.y=2(x+2)2﹣2 B.y=2(x+2)2+2 C.y=2(x﹣2)2﹣2D.y=2(x﹣2)2+221·世纪*教育网
7、若抛物线y=x2﹣2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( ) www-2-1-cnjy-com
A.y=(x﹣2)2+3 B.y=x2﹣1 C.y=(x﹣2)2+5 D.y=x2+4
8、若抛物线y=x2﹣2x+m的最低点的纵坐标为n,则m﹣n的值是( )
A.﹣1 B.0 C.1 D.2
9、已知二次函数y1=﹣3x2,,,它们的图象开口由小到大的顺序是( )
A.y1<y2<y3 B.y3<y2<y1 C.y1<y3<y2 D.y2<y3<y1
10、二次函数y=ax2+bx+c,自变量x与函数y的对应值如下表:
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
…
y
…
4
0
﹣2
﹣2
0
4
…
下列说法正确的是( )
A.抛物线的开口向下 B.当x>﹣3时,y随x的增大而增大
C.二次函数的最小值是﹣2 D.抛物线的对称轴x=﹣
11、二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣6
0
4
6
6
…
给出下列说法:
①抛物线与y轴的交点为(0,6); ②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点; ④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( ) A.4 B.3 C.2 D.1
12、若二次函数y=x2﹣6x+c的图象过A(﹣1,y1),B(3,y2),C(3+,y3),则y1,y2,y3的大小关系是( )21教育网
A.y1>y2>y3 B.y1>y3>y2 C.y2>y1>y3 D.y3>y1>y2
13、已知(1,y1)、(﹣2,y2)、(﹣4,y3)都是抛物线y=﹣2ax2﹣8ax+3(a<0)图象上的点,则下列各式中正确的是( )21cnjy.com
A.y1<y3<y2 B.y3<y2<y1 C.y2<y3<y1 D.y1<y2<y3
14、已知抛物线y=a(x﹣1)2+k(a,k是常数,且a>0)上三点P1(﹣2,y1),P2(﹣1,y2),P3(2,y3),则( )2·1·c·n·j·y
A.y1>y2>y3 B.y3>y2>y1 C.y3>y1>y2 D.y2>y1>y3
15、若抛物线y=(x+1)2+c与y轴相交于点(0,﹣5),则y的最小值为( )
A.﹣6 B.6 C.﹣5 D.5
16、设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+1上的三点,则y1,y2,y3的大小关系为( )21世纪教育网版权所有
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y3>y1>y2
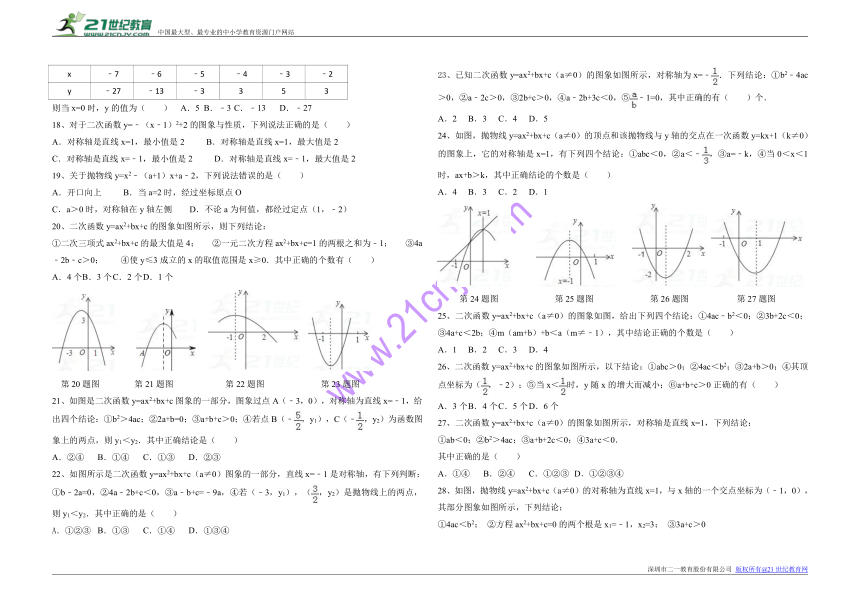
17、若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x
﹣7
﹣6
﹣5
﹣4
﹣3
﹣2
y
﹣27
﹣13
﹣3
3
5
3
则当x=0时,y的值为( ) A.5 B.﹣3 C.﹣13 D.﹣27
18、对于二次函数y=﹣(x﹣1)2+2的图象与性质,下列说法正确的是( )
A.对称轴是直线x=1,最小值是2 B.对称轴是直线x=1,最大值是2
C.对称轴是直线x=﹣1,最小值是2 D.对称轴是直线x=﹣1,最大值是2
19、关于抛物线y=x2﹣(a+1)x+a﹣2,下列说法错误的是( )
A.开口向上 B.当a=2时,经过坐标原点O
C.a>0时,对称轴在y轴左侧 D.不论a为何值,都经过定点(1,﹣2)
20、二次函数y=ax2+bx+c的图象如图所示,则下列结论:
①二次三项式ax2+bx+c的最大值是4; ②一元二次方程ax2+bx+c=1的两根之和为﹣1; ③4a﹣2b﹣c>0; ④使y≤3成立的x的取值范围是x≥0.其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
第20题图 第21题图 第22题图 第23题图
21、如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(﹣,y1),C(﹣,y2)为函数图象上的两点,则y1<y2.其中正确结论是( )
A.②④ B.①④ C.①③ D.②③
22、如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0,②4a﹣2b+c<0,③a﹣b+c=﹣9a,④若(﹣3,y1),(,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
①②③ B.①③ C.①④ D.①③④
23、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=﹣.下列结论:①b2﹣4ac>0,②a﹣2c>0,③2b+c>0,④a﹣2b+3c<0,⑤﹣1=0,其中正确的有( )个.
A.2 B.3 C.4 D.5
24、如图,抛物线y=ax2+bx+c(a≠0)的顶点和该抛物线与y轴的交点在一次函数y=kx+1(k≠0)的图象上,它的对称轴是x=1,有下列四个结论:①abc<0,②a<﹣,③a=﹣k,④当0<x<1时,ax+b>k,其中正确结论的个数是( )
A.4 B.3 C.2 D.1
第24题图 第25题图 第26题图 第27题图
25、二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠﹣1),其中结论正确的个数是( )
A.1 B.2 C.3 D.4
26、二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(,﹣2);⑤当x<时,y随x的增大而减小;⑥a+b+c>0正确的有( )
A.3个 B.4个 C.5个 D.6个
27、二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.
其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
28、如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2; ②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3 ⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A.4个 B.3个 C.2个 D.1个
第28题图 第29题图 第30题图 第31题图
29、二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1).下列结论:①2a+b>0;②abc<0; ③若OC=2OA,则2b﹣ac=4; ④3a﹣c<0.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
30、如图,抛物线y1=(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
31、如图,将函数y=(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
A. B. C. D.
32、已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A.B. C. D.
33、函数y=x2+bx+c与y=x的图象如图所示,有以下结论①b2﹣4c≥0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为( )
A.1 B.2 C.3 D.4
34、对于下列结论:
①二次函数y=6x2,当x>0时,y随x的增大而增大.
②关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是x1=﹣4,x2=﹣1.
③设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是c≥3.
其中,正确结论的个数是( )
A.0个 B.1个 C.2个 D.3个
35、已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1,0),且﹣1<x1<0,有下列5个结论:①abc>0;②9a﹣3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
36、二次函数y=x2﹣2x﹣3,当m﹣2≤x≤m时的最大值为5,则m的值可能为( )
A.0或6 B.4或﹣2 C.0或4 D.6或﹣2
37、已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )
A.3﹣或1+ B.3﹣或3+ C.3+或1﹣ D.1﹣或1+
38、已知二次函数y1=ax2+bx+c(b≠c)图象的最高点坐标为(﹣2,4),则一次函数y2=(b﹣c)x+b2﹣4ac图象可能在( )
A.一、二、三象限 B.一、二、四象限 C.一、三、四象限 D.二、三、四象限
39、已知关于x的二次函数y=x2+(1﹣a)x+1,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A.a=5 B.a≥5 C.a=3 D.a≥3
40、已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是( )
A. B. C.或 D.或
41、如图,二次函数y=x2﹣x,图象过△ABC三个顶点,其中A(﹣1,m),B(n,n)
求:①求A,B坐标;
②求△AOB的面积.
42、如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,与x轴交于点A(﹣2,0).
(1)求此二次函数的顶点B的坐标;
(2)在抛物线上有一点P,满足S△AOP=1,请直接写出点P的坐标.
43、如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?
44、已知:抛物线y=x2+4x+4+m的图象与y轴交于点C,点B与点C的纵坐标相同,一次函数y=kx+b的与二次函数交于A、B两点,且A点坐标为(﹣1,0).
(1)求二次函数与一次函数的解析式;
(2)若抛物线对称轴上存在一点P,直线PC将△ABC分成面积为1:2两部分,求P点坐标.
1、将二次函数y=x2+2x﹣1的图象沿x轴向右平移2个单位长度,得到的函数表达式是( )
A.y=(x+3)2﹣2 B.y=(x+3)2+2 C.y=(x﹣1)2+2 D.y=(x﹣1)2﹣221·cn·jy·com
2、已知关于x的方程只有一个实数根,则实数a的取值范围是( )
A.a>0 B.a<0 C.a≠0 D.a为一切实数
3、若(2,5),(4,5)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是( )
A.x=1 B.x=2 C.x=3 D.x=4
4、关于二次函数y=﹣2x2+1的图象,下列说法中,正确的是( )
A.对称轴为直线x=1 B.顶点坐标为(﹣2,1)
C.可以由二次函数y=﹣2x2的图象向左平移1个单位得到
D.在y轴的左侧,图象上升,在y轴的右侧,图象下降
5、下列函数中:①y=﹣3x;②y=2x﹣1;③;④y=﹣x2+2x+3(x>2),y的值随着x的增大而增大的函数个数有( )www.21-cn-jy.com
A.4个 B.3个 C.2个 D.1个
6、在平面直角坐标系x′O′y′中,如果抛物线y′=2x′2不动,而把x轴、y轴分别向下、向左平移2个单位,则在新坐标系下抛物线的表达式为( )【来源:21·世纪·教育·网】
A.y=2(x+2)2﹣2 B.y=2(x+2)2+2 C.y=2(x﹣2)2﹣2D.y=2(x﹣2)2+221·世纪*教育网
7、若抛物线y=x2﹣2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( ) www-2-1-cnjy-com
A.y=(x﹣2)2+3 B.y=x2﹣1 C.y=(x﹣2)2+5 D.y=x2+4
8、若抛物线y=x2﹣2x+m的最低点的纵坐标为n,则m﹣n的值是( )
A.﹣1 B.0 C.1 D.2
9、已知二次函数y1=﹣3x2,,,它们的图象开口由小到大的顺序是( )
A.y1<y2<y3 B.y3<y2<y1 C.y1<y3<y2 D.y2<y3<y1
10、二次函数y=ax2+bx+c,自变量x与函数y的对应值如下表:
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
…
y
…
4
0
﹣2
﹣2
0
4
…
下列说法正确的是( )
A.抛物线的开口向下 B.当x>﹣3时,y随x的增大而增大
C.二次函数的最小值是﹣2 D.抛物线的对称轴x=﹣
11、二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣6
0
4
6
6
…
给出下列说法:
①抛物线与y轴的交点为(0,6); ②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点; ④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( ) A.4 B.3 C.2 D.1
12、若二次函数y=x2﹣6x+c的图象过A(﹣1,y1),B(3,y2),C(3+,y3),则y1,y2,y3的大小关系是( )21教育网
A.y1>y2>y3 B.y1>y3>y2 C.y2>y1>y3 D.y3>y1>y2
13、已知(1,y1)、(﹣2,y2)、(﹣4,y3)都是抛物线y=﹣2ax2﹣8ax+3(a<0)图象上的点,则下列各式中正确的是( )21cnjy.com
A.y1<y3<y2 B.y3<y2<y1 C.y2<y3<y1 D.y1<y2<y3
14、已知抛物线y=a(x﹣1)2+k(a,k是常数,且a>0)上三点P1(﹣2,y1),P2(﹣1,y2),P3(2,y3),则( )2·1·c·n·j·y
A.y1>y2>y3 B.y3>y2>y1 C.y3>y1>y2 D.y2>y1>y3
15、若抛物线y=(x+1)2+c与y轴相交于点(0,﹣5),则y的最小值为( )
A.﹣6 B.6 C.﹣5 D.5
16、设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+1上的三点,则y1,y2,y3的大小关系为( )21世纪教育网版权所有
A.y1>y2>y3 B.y1>y3>y2 C.y3>y2>y1 D.y3>y1>y2
17、若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x
﹣7
﹣6
﹣5
﹣4
﹣3
﹣2
y
﹣27
﹣13
﹣3
3
5
3
则当x=0时,y的值为( ) A.5 B.﹣3 C.﹣13 D.﹣27
18、对于二次函数y=﹣(x﹣1)2+2的图象与性质,下列说法正确的是( )
A.对称轴是直线x=1,最小值是2 B.对称轴是直线x=1,最大值是2
C.对称轴是直线x=﹣1,最小值是2 D.对称轴是直线x=﹣1,最大值是2
19、关于抛物线y=x2﹣(a+1)x+a﹣2,下列说法错误的是( )
A.开口向上 B.当a=2时,经过坐标原点O
C.a>0时,对称轴在y轴左侧 D.不论a为何值,都经过定点(1,﹣2)
20、二次函数y=ax2+bx+c的图象如图所示,则下列结论:
①二次三项式ax2+bx+c的最大值是4; ②一元二次方程ax2+bx+c=1的两根之和为﹣1; ③4a﹣2b﹣c>0; ④使y≤3成立的x的取值范围是x≥0.其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
第20题图 第21题图 第22题图 第23题图
21、如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(﹣,y1),C(﹣,y2)为函数图象上的两点,则y1<y2.其中正确结论是( )
A.②④ B.①④ C.①③ D.②③
22、如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0,②4a﹣2b+c<0,③a﹣b+c=﹣9a,④若(﹣3,y1),(,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
①②③ B.①③ C.①④ D.①③④
23、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=﹣.下列结论:①b2﹣4ac>0,②a﹣2c>0,③2b+c>0,④a﹣2b+3c<0,⑤﹣1=0,其中正确的有( )个.
A.2 B.3 C.4 D.5
24、如图,抛物线y=ax2+bx+c(a≠0)的顶点和该抛物线与y轴的交点在一次函数y=kx+1(k≠0)的图象上,它的对称轴是x=1,有下列四个结论:①abc<0,②a<﹣,③a=﹣k,④当0<x<1时,ax+b>k,其中正确结论的个数是( )
A.4 B.3 C.2 D.1
第24题图 第25题图 第26题图 第27题图
25、二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠﹣1),其中结论正确的个数是( )
A.1 B.2 C.3 D.4
26、二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(,﹣2);⑤当x<时,y随x的增大而减小;⑥a+b+c>0正确的有( )
A.3个 B.4个 C.5个 D.6个
27、二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.
其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
28、如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2; ②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3 ⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A.4个 B.3个 C.2个 D.1个
第28题图 第29题图 第30题图 第31题图
29、二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1).下列结论:①2a+b>0;②abc<0; ③若OC=2OA,则2b﹣ac=4; ④3a﹣c<0.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
30、如图,抛物线y1=(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
31、如图,将函数y=(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
A. B. C. D.
32、已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A.B. C. D.
33、函数y=x2+bx+c与y=x的图象如图所示,有以下结论①b2﹣4c≥0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为( )
A.1 B.2 C.3 D.4
34、对于下列结论:
①二次函数y=6x2,当x>0时,y随x的增大而增大.
②关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是x1=﹣4,x2=﹣1.
③设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是c≥3.
其中,正确结论的个数是( )
A.0个 B.1个 C.2个 D.3个
35、已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1,0),且﹣1<x1<0,有下列5个结论:①abc>0;②9a﹣3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
36、二次函数y=x2﹣2x﹣3,当m﹣2≤x≤m时的最大值为5,则m的值可能为( )
A.0或6 B.4或﹣2 C.0或4 D.6或﹣2
37、已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )
A.3﹣或1+ B.3﹣或3+ C.3+或1﹣ D.1﹣或1+
38、已知二次函数y1=ax2+bx+c(b≠c)图象的最高点坐标为(﹣2,4),则一次函数y2=(b﹣c)x+b2﹣4ac图象可能在( )
A.一、二、三象限 B.一、二、四象限 C.一、三、四象限 D.二、三、四象限
39、已知关于x的二次函数y=x2+(1﹣a)x+1,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是( )
A.a=5 B.a≥5 C.a=3 D.a≥3
40、已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是( )
A. B. C.或 D.或
41、如图,二次函数y=x2﹣x,图象过△ABC三个顶点,其中A(﹣1,m),B(n,n)
求:①求A,B坐标;
②求△AOB的面积.
42、如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,与x轴交于点A(﹣2,0).
(1)求此二次函数的顶点B的坐标;
(2)在抛物线上有一点P,满足S△AOP=1,请直接写出点P的坐标.
43、如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?
44、已知:抛物线y=x2+4x+4+m的图象与y轴交于点C,点B与点C的纵坐标相同,一次函数y=kx+b的与二次函数交于A、B两点,且A点坐标为(﹣1,0).
(1)求二次函数与一次函数的解析式;
(2)若抛物线对称轴上存在一点P,直线PC将△ABC分成面积为1:2两部分,求P点坐标.
