5.1.1 相交线 (课件)
图片预览






文档简介
(共18张PPT)
相 交 线
人教版 七年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
问题:在我们的生活世界中,蕴涵着大量的相交线和平行线,大家对它们也不陌生,请找出图片中的相交线、平行线.
新课导入
定义探究
例题精讲
再探新知
拓展练习
课堂小结
导 航
导入新课
问题:在我们的生活世界中,蕴涵着大量的相交线和平行线,大家对它们也不陌生,请找出图片中的相交线、平行线.
新课讲解
你能再找出一些身边的相交线、平行线的实例吗?
比如,教室里黑板面相邻的两条边、相对的两条边,操场上的双杠,方格纸上的横线和竖线等等,都给人以相交线、平行线的形象.
新课导入
定义探究
例题精讲
再探新知
拓展练习
课堂小结
导 航
新课讲解
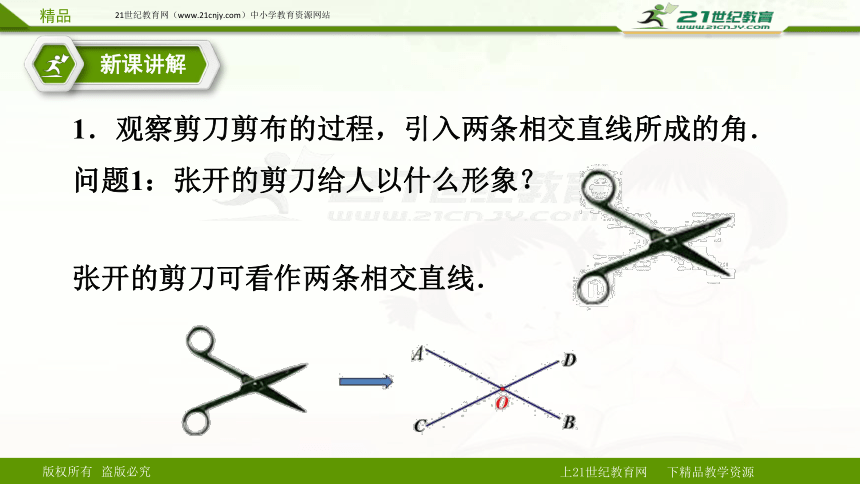
1.观察剪刀剪布的过程,引入两条相交直线所成的角.
问题1:张开的剪刀给人以什么形象?
张开的剪刀可看作两条相交直线.
新课讲解
问题2:两个把手之间的角发生了什么变化?剪刀刀刃张开的口又怎么变化?
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刀刃之间的角也相应变小.
如果改变用力方向,随着两个把手之间的角逐渐变大,剪刀刀刃之间的角也相应变大.
新课讲解
2.认识邻补角和对顶角,探索它们的性质
(1)角的位置关系
问题 3:画直线AB,CD相交于点O,并说出图中4个角,各对角的位置关系如何?根据不同的位置怎么命名?(完成表格中的前三项)
新课讲解
两直线相交 所形成的角 分类 位置关系 数量关系
∠1
∠2
∠3
∠4
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
邻补角
对顶角
4
3
1
2
A
B
C
O
D
新课讲解
讨论结果:∠AOC和∠BOC有一条公共边OC,它们的另一边互为反向延长线;
∠AOC和∠BOD有公共的顶点O,而∠AOC的两边分别是∠BOD两边的反向延长线.
邻补角、对顶角的概念:有一条公共边,并且它们的另一边互为反向延长线的两个角叫做邻补角.
如果两个角有一个公共顶点,并且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫做对顶角.
新课讲解
初步应用:
判断题
①邻补角可看成是平角被过它顶点的一条射线分成的两个角.( )
②有公共顶点,没有公共边的角是对顶角.( )
√
×
新课讲解
问题4:用量角器分别量一量各个角的度数,你发现各类角的度数有什么关系?(完成表格的第四项内容)
两直线相交 所形成的角 分类 位置关系 数量关系
互补
相等
∠1
∠2
∠3
∠4
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
邻补角
对顶角
4
3
1
2
A
B
C
O
D
问题5:能不能用所学知识说明邻补角的和为什么是180°,对顶角为什么相等?
讨论结果:在问题3图中,∠AOC的邻补角是∠BOC和∠AOD,所以∠AOC与∠BOC互补,∠AOC与∠AOD互补,根据“同角的补角相等”,可以得出∠AOD=∠BOC,类似地有∠AOC=∠BOD.
对顶角的性质:对顶角相等.
A
B
C
O
D
新课讲解
例 如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
解:由邻补角的定义,得
∠2=180°-∠1=180°-40°=140°;
由对顶角相等,得
∠3=∠1=40°,
∠4=∠2=140°.
4
3
1
2
a
b
新课讲解
1.判断下列图中∠1、∠2是否是对顶角.
A B C D
×
√
×
×
巩固练习
2.如图,直线a,b相交,
(1)当∠1=40°时,求∠2,∠3,∠4的度数;
(2)当∠1=90°时,求∠2,∠3,∠4的度数.
解:(1)140°; 40°; 140°;
(2)90°; 90°; 90°.
4
3
1
2
a
b
巩固练习
1.本节主要学习了邻补角、对顶角的概念以及对顶角的性质.
2.要学会在较复杂的图形中识别邻补角、对顶角.
3.不仅会用对顶角的性质解决问题,还要知道新知识是如何得出的,在解决问题的过程中注意训练说理能力.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
相 交 线
人教版 七年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
问题:在我们的生活世界中,蕴涵着大量的相交线和平行线,大家对它们也不陌生,请找出图片中的相交线、平行线.
新课导入
定义探究
例题精讲
再探新知
拓展练习
课堂小结
导 航
导入新课
问题:在我们的生活世界中,蕴涵着大量的相交线和平行线,大家对它们也不陌生,请找出图片中的相交线、平行线.
新课讲解
你能再找出一些身边的相交线、平行线的实例吗?
比如,教室里黑板面相邻的两条边、相对的两条边,操场上的双杠,方格纸上的横线和竖线等等,都给人以相交线、平行线的形象.
新课导入
定义探究
例题精讲
再探新知
拓展练习
课堂小结
导 航
新课讲解
1.观察剪刀剪布的过程,引入两条相交直线所成的角.
问题1:张开的剪刀给人以什么形象?
张开的剪刀可看作两条相交直线.
新课讲解
问题2:两个把手之间的角发生了什么变化?剪刀刀刃张开的口又怎么变化?
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刀刃之间的角也相应变小.
如果改变用力方向,随着两个把手之间的角逐渐变大,剪刀刀刃之间的角也相应变大.
新课讲解
2.认识邻补角和对顶角,探索它们的性质
(1)角的位置关系
问题 3:画直线AB,CD相交于点O,并说出图中4个角,各对角的位置关系如何?根据不同的位置怎么命名?(完成表格中的前三项)
新课讲解
两直线相交 所形成的角 分类 位置关系 数量关系
∠1
∠2
∠3
∠4
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
邻补角
对顶角
4
3
1
2
A
B
C
O
D
新课讲解
讨论结果:∠AOC和∠BOC有一条公共边OC,它们的另一边互为反向延长线;
∠AOC和∠BOD有公共的顶点O,而∠AOC的两边分别是∠BOD两边的反向延长线.
邻补角、对顶角的概念:有一条公共边,并且它们的另一边互为反向延长线的两个角叫做邻补角.
如果两个角有一个公共顶点,并且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫做对顶角.
新课讲解
初步应用:
判断题
①邻补角可看成是平角被过它顶点的一条射线分成的两个角.( )
②有公共顶点,没有公共边的角是对顶角.( )
√
×
新课讲解
问题4:用量角器分别量一量各个角的度数,你发现各类角的度数有什么关系?(完成表格的第四项内容)
两直线相交 所形成的角 分类 位置关系 数量关系
互补
相等
∠1
∠2
∠3
∠4
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
邻补角
对顶角
4
3
1
2
A
B
C
O
D
问题5:能不能用所学知识说明邻补角的和为什么是180°,对顶角为什么相等?
讨论结果:在问题3图中,∠AOC的邻补角是∠BOC和∠AOD,所以∠AOC与∠BOC互补,∠AOC与∠AOD互补,根据“同角的补角相等”,可以得出∠AOD=∠BOC,类似地有∠AOC=∠BOD.
对顶角的性质:对顶角相等.
A
B
C
O
D
新课讲解
例 如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
解:由邻补角的定义,得
∠2=180°-∠1=180°-40°=140°;
由对顶角相等,得
∠3=∠1=40°,
∠4=∠2=140°.
4
3
1
2
a
b
新课讲解
1.判断下列图中∠1、∠2是否是对顶角.
A B C D
×
√
×
×
巩固练习
2.如图,直线a,b相交,
(1)当∠1=40°时,求∠2,∠3,∠4的度数;
(2)当∠1=90°时,求∠2,∠3,∠4的度数.
解:(1)140°; 40°; 140°;
(2)90°; 90°; 90°.
4
3
1
2
a
b
巩固练习
1.本节主要学习了邻补角、对顶角的概念以及对顶角的性质.
2.要学会在较复杂的图形中识别邻补角、对顶角.
3.不仅会用对顶角的性质解决问题,还要知道新知识是如何得出的,在解决问题的过程中注意训练说理能力.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
