6.1平方根 第二课时(课件)
图片预览






文档简介
(共20张PPT)
平方根 第二课时
人教版 七年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
我们已经知道:正数x满足x2=a,则称x是a的算术平方根,当a恰是一个数的平方数时,我们已经能求出它的算术平方根了,例如,
;但当a不是一个数的平方数时,它的算术平方根又该怎样求呢?
导入新课
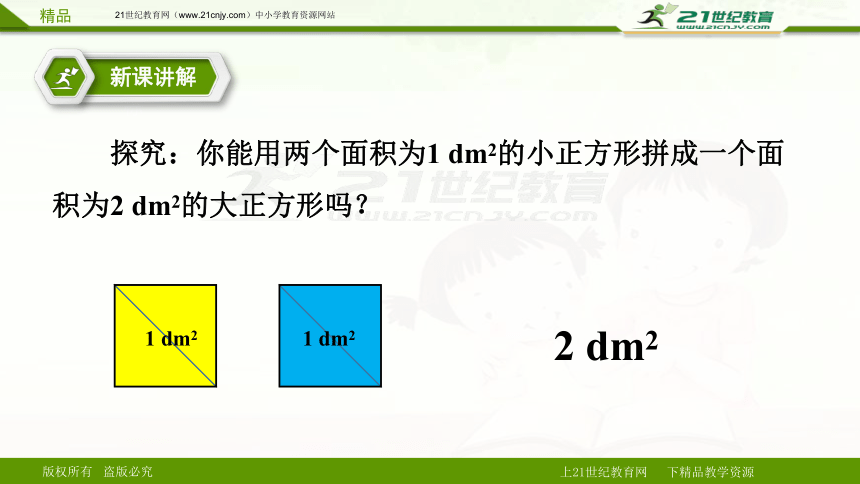
探究:你能用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形吗?
1 dm2
1 dm2
2 dm2
教学目标
新课讲解
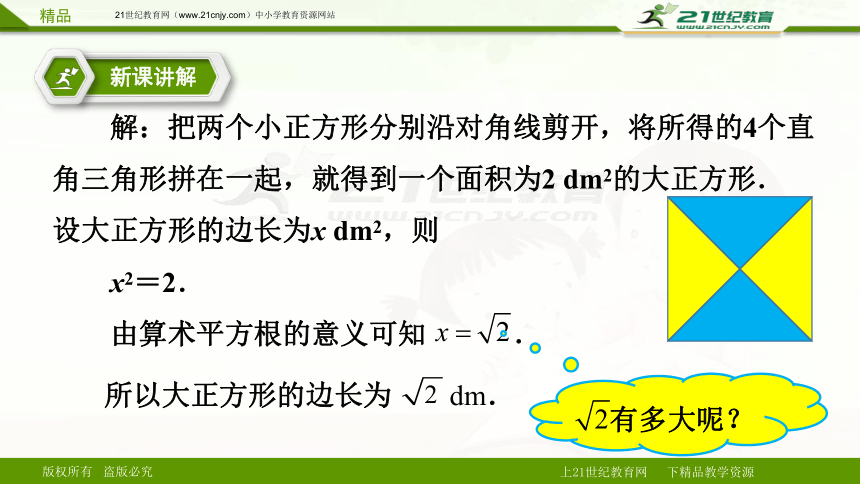
解:把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2 dm2的大正方形.
设大正方形的边长为x dm2,则
x2=2.
由算术平方根的意义可知 .
有多大呢?
所以大正方形的边长为 dm.
教学目标
新课讲解
你是怎样判断出 大于1而小于2的?
因为12=1,22=4 ,
而1<2<4 ,
所以 .
你能不能得到 的更精确的范围?
大于1而小于2
有多大呢?
教学目标
新课讲解
因为1.42=1.96, 1.52=2.25,
因为1.412=1.988 1,1.422=2.016 4 ,
而 1.988 1<2<2.016 4 ,
而 ,
所以 1.4< <1.5 ;
所以 1.41< <1.42 ;
教学目标
新课讲解
……
因为 1.4142=1.999396 , 1.4152=2.002225,
而 1.999 369<2<2.002 225 ,
所以 1.414< <1.415;
是一个无限不循环小数.
无限不循环小数是指小数位数无限,且小数部分为不循环的小数.
教学目标
新课讲解
用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
解:(1)依次按键 3 136 显示:56.
∴ =56.
(2)依次按键 2 显示:1.414213562.
∴
教学目标
新课讲解
… …
… …
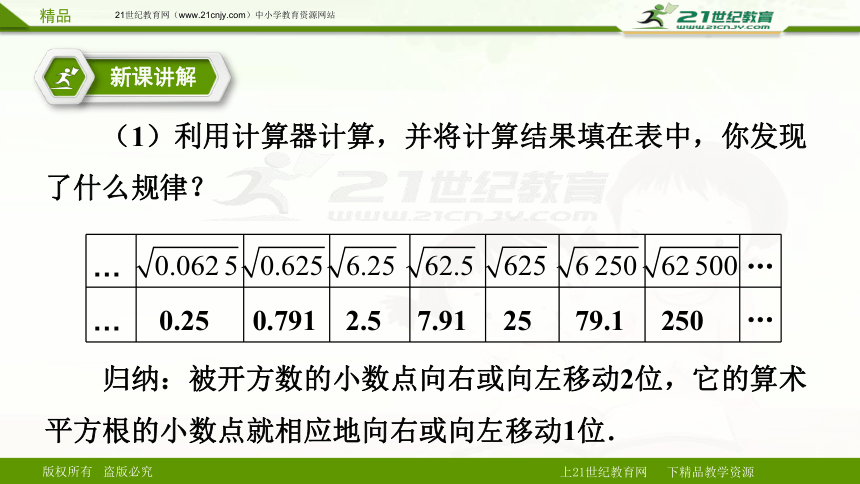
(1)利用计算器计算,并将计算结果填在表中,你发现了什么规律?
0.25
0.791
2.5
25
7.91
79.1
250
归纳:被开方数的小数点向右或向左移动2位,它的算术平方根的小数点就相应地向右或向左移动1位.
教学目标
新课讲解
道理是:从被开方数扩大的倍数与其算术平方根扩大的倍数思考回答.即当被开方数扩大(或缩小)100倍,10 000倍…时,其算术平方根相应地扩大(或缩小)10倍,100倍….
教学目标
新课讲解
(2)你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
解:因为 ;
所以 ; ; .
解:因为被开方数30与3不符合上述规律,
所以无法由 的值说出 的值.
(3)你能否根据 的值说出 是多少?
教学目标
新课讲解
小丽想用一块面积为400 cm2为的正方形纸片,沿着边的方向裁出一块面积为300 cm2的长方形纸片,使它的长宽之比为3∶2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
你能将这个问题转化为数学问题吗?
教学目标
新课讲解
解:设剪出的长方形的两边长分别为3x cm和2x cm, 则有3x 2x=300, 6x2=300,
x2=50, .
故长方形纸片的长为 ,宽为 .
出示问题:
(1)你能将这个问题转化为数学问题吗?
(2)如何求出长方形的长和宽?
(3)长方形的长和宽与正方形的边长之间的大小关系是什么?
教学目标
新课讲解
因为 50>49,得 >7 ,
所以 >3×7=21,
大于原正方形的边长,这是不可能的.所以,小丽不能用这块纸片裁出符合要求的纸片.
长方形的长和宽与正方形的边长之间的大小关系是什么?小丽能用这块纸片裁出符合要求的纸片吗?
教学目标
新课讲解
1.若x是 的算术平方根,则x=( ).
A.7 B. C.49 D.
2.若 , ,那么 ;
11.18
__________.
0.3535
B
巩固练习
3.用计算器求下列各式的值:
(1) ;(2) ;(3) (精确到0.01).
(2) ;
解(1) ;
(3) .
巩固练习
4.比较下列各组数的大小:
(1) 与12;(2) 与0.5.
解:(1)因为 ,而 ,
所以 .
(2)因为 ,而 ,
所以 .
巩固练习
1.被开方数扩大或缩小时,其相应的算术平方根也扩大或缩小,因此我们可以利用夹值的方法来求出算术平方根的近似值.
2.利用计算器可以求出任意正数的算术平方根的近似值.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
平方根 第二课时
人教版 七年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
我们已经知道:正数x满足x2=a,则称x是a的算术平方根,当a恰是一个数的平方数时,我们已经能求出它的算术平方根了,例如,
;但当a不是一个数的平方数时,它的算术平方根又该怎样求呢?
导入新课
探究:你能用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形吗?
1 dm2
1 dm2
2 dm2
教学目标
新课讲解
解:把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2 dm2的大正方形.
设大正方形的边长为x dm2,则
x2=2.
由算术平方根的意义可知 .
有多大呢?
所以大正方形的边长为 dm.
教学目标
新课讲解
你是怎样判断出 大于1而小于2的?
因为12=1,22=4 ,
而1<2<4 ,
所以 .
你能不能得到 的更精确的范围?
大于1而小于2
有多大呢?
教学目标
新课讲解
因为1.42=1.96, 1.52=2.25,
因为1.412=1.988 1,1.422=2.016 4 ,
而 1.988 1<2<2.016 4 ,
而 ,
所以 1.4< <1.5 ;
所以 1.41< <1.42 ;
教学目标
新课讲解
……
因为 1.4142=1.999396 , 1.4152=2.002225,
而 1.999 369<2<2.002 225 ,
所以 1.414< <1.415;
是一个无限不循环小数.
无限不循环小数是指小数位数无限,且小数部分为不循环的小数.
教学目标
新课讲解
用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
解:(1)依次按键 3 136 显示:56.
∴ =56.
(2)依次按键 2 显示:1.414213562.
∴
教学目标
新课讲解
… …
… …
(1)利用计算器计算,并将计算结果填在表中,你发现了什么规律?
0.25
0.791
2.5
25
7.91
79.1
250
归纳:被开方数的小数点向右或向左移动2位,它的算术平方根的小数点就相应地向右或向左移动1位.
教学目标
新课讲解
道理是:从被开方数扩大的倍数与其算术平方根扩大的倍数思考回答.即当被开方数扩大(或缩小)100倍,10 000倍…时,其算术平方根相应地扩大(或缩小)10倍,100倍….
教学目标
新课讲解
(2)你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
解:因为 ;
所以 ; ; .
解:因为被开方数30与3不符合上述规律,
所以无法由 的值说出 的值.
(3)你能否根据 的值说出 是多少?
教学目标
新课讲解
小丽想用一块面积为400 cm2为的正方形纸片,沿着边的方向裁出一块面积为300 cm2的长方形纸片,使它的长宽之比为3∶2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
你能将这个问题转化为数学问题吗?
教学目标
新课讲解
解:设剪出的长方形的两边长分别为3x cm和2x cm, 则有3x 2x=300, 6x2=300,
x2=50, .
故长方形纸片的长为 ,宽为 .
出示问题:
(1)你能将这个问题转化为数学问题吗?
(2)如何求出长方形的长和宽?
(3)长方形的长和宽与正方形的边长之间的大小关系是什么?
教学目标
新课讲解
因为 50>49,得 >7 ,
所以 >3×7=21,
大于原正方形的边长,这是不可能的.所以,小丽不能用这块纸片裁出符合要求的纸片.
长方形的长和宽与正方形的边长之间的大小关系是什么?小丽能用这块纸片裁出符合要求的纸片吗?
教学目标
新课讲解
1.若x是 的算术平方根,则x=( ).
A.7 B. C.49 D.
2.若 , ,那么 ;
11.18
__________.
0.3535
B
巩固练习
3.用计算器求下列各式的值:
(1) ;(2) ;(3) (精确到0.01).
(2) ;
解(1) ;
(3) .
巩固练习
4.比较下列各组数的大小:
(1) 与12;(2) 与0.5.
解:(1)因为 ,而 ,
所以 .
(2)因为 ,而 ,
所以 .
巩固练习
1.被开方数扩大或缩小时,其相应的算术平方根也扩大或缩小,因此我们可以利用夹值的方法来求出算术平方根的近似值.
2.利用计算器可以求出任意正数的算术平方根的近似值.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
