8.2 消元—解二元一次方程组 第一课时(课件)
文档属性
| 名称 | 8.2 消元—解二元一次方程组 第一课时(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-13 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
消元 — 解二元一次方程组 第一课时
人教版 七年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
问题:运动会要到了,篮球是七(1)班的拳头项目.为了取得好名次,他们想在全部22场比赛中得到40分.已知每场比赛都要分出胜负,胜队得2分,负队得1分.那么七(1)班应该胜、负各几场?
你会用二元一次方程组解决这个问题吗?
根据问题中的等量关系设胜x场,负y场,可以更容易地列出方程
导入新课
x 0 1 2 3 4 5 6 7 8 … 17 18 19 20 21 22
y 22 21 20 19 18 17 16 15 14 … 5 4 3 2 1 0
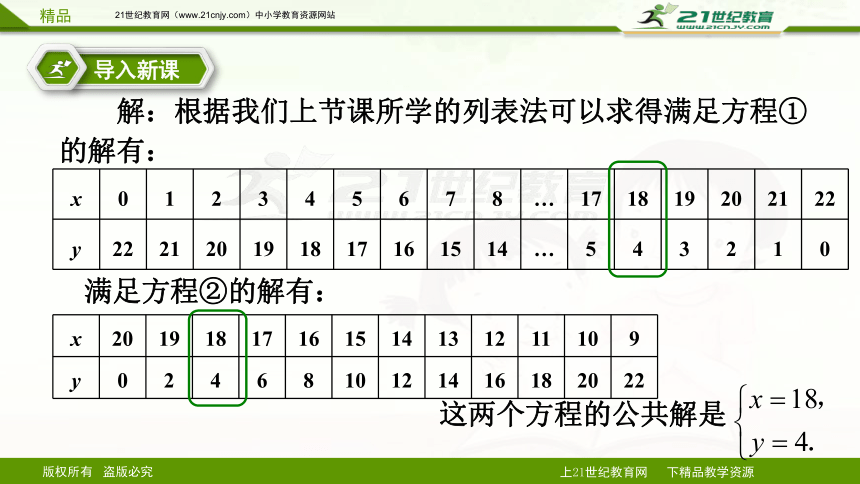
解:根据我们上节课所学的列表法可以求得满足方程①的解有:
x 20 19 18 17 16 15 14 13 12 11 10 9
y 0 2 4 6 8 10 12 14 16 18 20 22
满足方程②的解有:
这两个方程的公共解是
导入新课
设两个未知数:胜x场,负y场,可以列方程组
只设一个未知数:胜x场,可列一元一次方程
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
2x+(10-x)=16.
新课讲解
对比方程和方程组,你能发现它们之间的关系吗?
二元一次方程组中有两个未知数,如果消去其中一个未知数,将二元一次方程组转化为我们熟悉的一元一次方程,我们就可以先解出一个未知数,然后再设法求另一未知数.这种将未知数的个数由多化少、逐一解决的思想,叫做消元思想.
新课讲解
解方程组
解:
①
②
由①得:
③
把③代入②得:
1. 将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2. 用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
变
代
探究解法:
解得
新课讲解
把 代入③,得
3. 把这个未知数的值代入上面的式子,求得另一个未知数的值;
4. 写出方程组的解.
求
写
∴方程组的解是
新课讲解
上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法.
归 纳:
新课讲解
把下列方程写成用含x的式子表示y的形式:
(1)2x-y=3;
(2)3x+y-1=0.
解:(1)y=2x-3;
(2)y=1-3x.
新课讲解
例1 用代入法解方程组
分析:方程①中x的系数是1,用含y的式子表示x,比较简便.
新课讲解
所以这个方程组的解是
解:由①,得x=y+3. ③
把③代入②,得 (把③代入①可以吗?试试看)
3(y+3)-8y=14.
解这个方程,得y=-1.
把y=-1代入③,得 (把y=-1代入①或②可以吗?)
x=2.
新课讲解
例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量 (按瓶计算)比为2:5.某厂每天生产这种消毒液22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
分析:问题中包含两个条件:
大瓶数∶小瓶数=2∶5,
大瓶所装消毒液+小瓶所装消毒液=总生产量.
新课讲解
解:设这些消毒液应该分装x大瓶、y小瓶.
根据大、小瓶数的比以及消毒液分装量与总生产量的相等关系,得
由①,得
把③代入②,得
新课讲解
解这个方程,得x=20 000.
把x=20 000代入③,得y=50 000.
这个方程组的解是
答:这些消毒液应该分装20 000大瓶和50 000小瓶.
新课讲解
二元一次方程组
变形
代入
y=50 000
x=20 000
解得x
一元一次方程
消去y
用 代替y,
消去未知数y
上面解方程组的过程可以用下面的框图表示:
解得y
代入
新课讲解
解这个方程时,可以先消去x吗?试试看.
解:由①,得
把③代入②,得
解这个方程,得y=50 000.
新课讲解
把y=50 000代入③,得x=20 000.
这个方程组的解是
答:这些消毒液应该分装20 000大瓶和50 000小瓶.
新课讲解
1.用代入法解下列方程组:
(1)
(2)
解:(1)
把①代入②,得3x+2(2x-3)=8.
解这个方程,得x=2.
把x=2代入①,得y=1.
所以这个方程组的解是
1.用代入法解下列方程组:
(1)
(2)
解:(2)
由①,得y=2x-5. ③
把③代入②,得
3x+4(2x-5)=2.
解这个方程,得x=2.
把x=2代入③,得y=-1.
所以这个方程组的解是
巩固练习
2.有48支队520名运动员参加篮、排球比赛,其中每支篮球队10人,每支排球队12人,每名运动员只参加一项比赛.篮、排球队各有多少支参赛?
解:设篮球队有x支参赛、排球队有y支参赛.
根据题中的等量关系,列式得
巩固练习
由①,得y=48-x. ③
把③代入②,得
解这个方程,得x=28.
把x=28代入③,得y=20.
答:篮球队有28支参赛、排球队有20支参赛.
所以这个方程组的解是
巩固练习
1.如何用代入法处理两个未知数的绝对值均不为1的二元一次方程组?
对于用代入法解未知数的绝对值均不为1的二元一次方程组,解题时,应选择未知数的系数绝对值比较小的一个方程进行变形,这样可使运算简便.
课堂小结
2.列二元一次方程组解应用题的关键是:找出两个等量关系.
3.列二元一次方程组解应用题的一般步骤分为:审、设、列、解、检、答.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪
教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
消元 — 解二元一次方程组 第一课时
人教版 七年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
问题:运动会要到了,篮球是七(1)班的拳头项目.为了取得好名次,他们想在全部22场比赛中得到40分.已知每场比赛都要分出胜负,胜队得2分,负队得1分.那么七(1)班应该胜、负各几场?
你会用二元一次方程组解决这个问题吗?
根据问题中的等量关系设胜x场,负y场,可以更容易地列出方程
导入新课
x 0 1 2 3 4 5 6 7 8 … 17 18 19 20 21 22
y 22 21 20 19 18 17 16 15 14 … 5 4 3 2 1 0
解:根据我们上节课所学的列表法可以求得满足方程①的解有:
x 20 19 18 17 16 15 14 13 12 11 10 9
y 0 2 4 6 8 10 12 14 16 18 20 22
满足方程②的解有:
这两个方程的公共解是
导入新课
设两个未知数:胜x场,负y场,可以列方程组
只设一个未知数:胜x场,可列一元一次方程
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
2x+(10-x)=16.
新课讲解
对比方程和方程组,你能发现它们之间的关系吗?
二元一次方程组中有两个未知数,如果消去其中一个未知数,将二元一次方程组转化为我们熟悉的一元一次方程,我们就可以先解出一个未知数,然后再设法求另一未知数.这种将未知数的个数由多化少、逐一解决的思想,叫做消元思想.
新课讲解
解方程组
解:
①
②
由①得:
③
把③代入②得:
1. 将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2. 用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
变
代
探究解法:
解得
新课讲解
把 代入③,得
3. 把这个未知数的值代入上面的式子,求得另一个未知数的值;
4. 写出方程组的解.
求
写
∴方程组的解是
新课讲解
上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法.
归 纳:
新课讲解
把下列方程写成用含x的式子表示y的形式:
(1)2x-y=3;
(2)3x+y-1=0.
解:(1)y=2x-3;
(2)y=1-3x.
新课讲解
例1 用代入法解方程组
分析:方程①中x的系数是1,用含y的式子表示x,比较简便.
新课讲解
所以这个方程组的解是
解:由①,得x=y+3. ③
把③代入②,得 (把③代入①可以吗?试试看)
3(y+3)-8y=14.
解这个方程,得y=-1.
把y=-1代入③,得 (把y=-1代入①或②可以吗?)
x=2.
新课讲解
例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量 (按瓶计算)比为2:5.某厂每天生产这种消毒液22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
分析:问题中包含两个条件:
大瓶数∶小瓶数=2∶5,
大瓶所装消毒液+小瓶所装消毒液=总生产量.
新课讲解
解:设这些消毒液应该分装x大瓶、y小瓶.
根据大、小瓶数的比以及消毒液分装量与总生产量的相等关系,得
由①,得
把③代入②,得
新课讲解
解这个方程,得x=20 000.
把x=20 000代入③,得y=50 000.
这个方程组的解是
答:这些消毒液应该分装20 000大瓶和50 000小瓶.
新课讲解
二元一次方程组
变形
代入
y=50 000
x=20 000
解得x
一元一次方程
消去y
用 代替y,
消去未知数y
上面解方程组的过程可以用下面的框图表示:
解得y
代入
新课讲解
解这个方程时,可以先消去x吗?试试看.
解:由①,得
把③代入②,得
解这个方程,得y=50 000.
新课讲解
把y=50 000代入③,得x=20 000.
这个方程组的解是
答:这些消毒液应该分装20 000大瓶和50 000小瓶.
新课讲解
1.用代入法解下列方程组:
(1)
(2)
解:(1)
把①代入②,得3x+2(2x-3)=8.
解这个方程,得x=2.
把x=2代入①,得y=1.
所以这个方程组的解是
1.用代入法解下列方程组:
(1)
(2)
解:(2)
由①,得y=2x-5. ③
把③代入②,得
3x+4(2x-5)=2.
解这个方程,得x=2.
把x=2代入③,得y=-1.
所以这个方程组的解是
巩固练习
2.有48支队520名运动员参加篮、排球比赛,其中每支篮球队10人,每支排球队12人,每名运动员只参加一项比赛.篮、排球队各有多少支参赛?
解:设篮球队有x支参赛、排球队有y支参赛.
根据题中的等量关系,列式得
巩固练习
由①,得y=48-x. ③
把③代入②,得
解这个方程,得x=28.
把x=28代入③,得y=20.
答:篮球队有28支参赛、排球队有20支参赛.
所以这个方程组的解是
巩固练习
1.如何用代入法处理两个未知数的绝对值均不为1的二元一次方程组?
对于用代入法解未知数的绝对值均不为1的二元一次方程组,解题时,应选择未知数的系数绝对值比较小的一个方程进行变形,这样可使运算简便.
课堂小结
2.列二元一次方程组解应用题的关键是:找出两个等量关系.
3.列二元一次方程组解应用题的一般步骤分为:审、设、列、解、检、答.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪
教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
