9.2一元一次不等式 第一课时 (课件)
文档属性
| 名称 | 9.2一元一次不等式 第一课时 (课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-13 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
一元一次不等式 第一课时
人教版 七年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
解决下列思考题:
(1)什么叫做不等式的解?说出不等式2x<-4的一个解.
使不等式成立的未知数的值叫做不等式的解.-3就是不等
式2x<-4的一个解.
(2)什么叫做不等式的解集?不等式2x<-4的解集是什
么?
能使不等式成立的未知数的取值范围,叫做不等式的解的集合,简称解集.2x<-4的解集是x<-2.
导入新课
(3)什么叫解不等式?请解不等式-2x>7.
求不等式的解集的过程叫做解不等式.
解:-2x>7.根据不等式的性质3,不等式两边同除以-2,不等式的符号改变,得:
即
导入新课
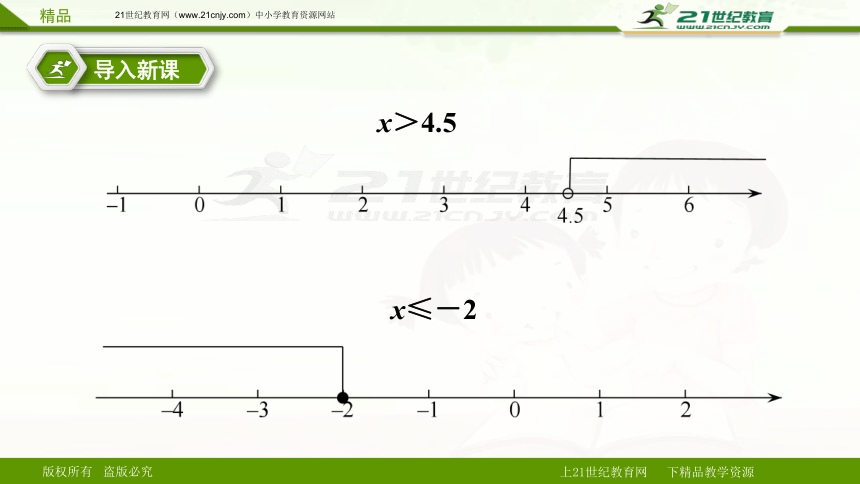
(4)将不等式的解集在数轴上表示时,向左画表示什么?向右画表示什么?实心圆点表示什么?空心圆圈表示什么?请将x>4.5,x≤-2在数轴上表示出来.
将不等式的解集在数轴上表示时,向左画表示大于,向右画表示小于,实心圆点表示包括这个点,空心圆圈表示不包括这个点.
导入新课
x>4.5
x≤-2
导入新课
(5)什么叫做一元一次方程?2x-y=2是吗?a=1是吗?
含有一个未知数、未知数的次数是1的方程,叫做一元一次方程.
2x-y=2不是一元一次方程,a=1是一元一次方程.
导入新课
观察下面的不等式:
x-7>26,3x<2x+1, ,-4x>3.
它们有哪些共同特征?
可以发现,上述每个不等式只含有一个未知数,并且未知数的次数是1.类似于一元一次方程.含有一个未知数、未知数的次数是1的不等式,叫做一元一次不等式.
新课讲解
上节课我们知道,不等式x-7>26的解集是x>33.
总结归纳:这个解集是通过“不等式两边都加7,不等号的方向不变”,而得到的.这相当于由x-7>26得x>26+7.这就是说,解不等式时也可以“移项”,即把不等式一边的某项变号后移到另一边,而不改变不等号的方向.
一般地,利用不等式的性质,采取与解一元一次方程相类似的步骤,就可以求出一元一次不等式的解集.
新课讲解
(1) ;(2) .
解下列不等式,并在数轴上表示解集:
解:(1)去括号,得 .
移项,得 .
合并同类项,得 .
系数化为1,得 .
新课讲解
0
这个不等式的解集在数轴上的表示如图所示:
新课讲解
解:(2)去分母,得 ,
去括号,得 ,
移项,得 ,
合并同类项,得 ,
系数化为1,得 .
这个不等式的解集在数轴上的表示如图所示:
0
8
新课讲解
特别注意,当不等式的两边都乘(或除以)同一个负数时,不等号的方向改变.
归纳:解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
新课讲解
①3x-1≥4; ② ③ ④
1.下列式子中,一元一次不等式有( ).
⑤
⑥
⑦
⑧
A.5个 B.4个 C.6个 D.3个
C
巩固练习
2.解下列不等式,并在数轴上表示不等式的解集.
(1)5x+15>4x-1;
(2)2(x+5)≤3(x-5);
(4) .
(3) ;
巩固练习
解:(1)移项,得5x-4x>-1-15.
合并同类项,得x>-16.
这个不等式的解集在数轴上的表示如图所示:
巩固练习
(2)去括号,得2x+10≤3x-15.
移项,得2x-3x≤-15-10.
合并同类项,得-x≤-25.
系数化为1,得x≥25.
这个不等式的解集在数轴上的表示如图所示:
巩固练习
(3)去分母,得
去括号,得
移项,得
合并同类项,得
这个不等式的解集在数轴上表示如图所示:
巩固练习
(4)去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
这个不等式的解集在数轴上表示如图所示:
巩固练习
1.一元一次不等式的定义:含有一个未知数,并且未知数的次数是1的不等式叫做一元一次不等式.
2.解一元一次不等式的步骤:
去分母、去括号、移项、合并同类项、将系数化为1.
要特别注意,当不等式的两边都乘(或除以)同一个负数时,不等号的方向改变.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪
教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
一元一次不等式 第一课时
人教版 七年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
解决下列思考题:
(1)什么叫做不等式的解?说出不等式2x<-4的一个解.
使不等式成立的未知数的值叫做不等式的解.-3就是不等
式2x<-4的一个解.
(2)什么叫做不等式的解集?不等式2x<-4的解集是什
么?
能使不等式成立的未知数的取值范围,叫做不等式的解的集合,简称解集.2x<-4的解集是x<-2.
导入新课
(3)什么叫解不等式?请解不等式-2x>7.
求不等式的解集的过程叫做解不等式.
解:-2x>7.根据不等式的性质3,不等式两边同除以-2,不等式的符号改变,得:
即
导入新课
(4)将不等式的解集在数轴上表示时,向左画表示什么?向右画表示什么?实心圆点表示什么?空心圆圈表示什么?请将x>4.5,x≤-2在数轴上表示出来.
将不等式的解集在数轴上表示时,向左画表示大于,向右画表示小于,实心圆点表示包括这个点,空心圆圈表示不包括这个点.
导入新课
x>4.5
x≤-2
导入新课
(5)什么叫做一元一次方程?2x-y=2是吗?a=1是吗?
含有一个未知数、未知数的次数是1的方程,叫做一元一次方程.
2x-y=2不是一元一次方程,a=1是一元一次方程.
导入新课
观察下面的不等式:
x-7>26,3x<2x+1, ,-4x>3.
它们有哪些共同特征?
可以发现,上述每个不等式只含有一个未知数,并且未知数的次数是1.类似于一元一次方程.含有一个未知数、未知数的次数是1的不等式,叫做一元一次不等式.
新课讲解
上节课我们知道,不等式x-7>26的解集是x>33.
总结归纳:这个解集是通过“不等式两边都加7,不等号的方向不变”,而得到的.这相当于由x-7>26得x>26+7.这就是说,解不等式时也可以“移项”,即把不等式一边的某项变号后移到另一边,而不改变不等号的方向.
一般地,利用不等式的性质,采取与解一元一次方程相类似的步骤,就可以求出一元一次不等式的解集.
新课讲解
(1) ;(2) .
解下列不等式,并在数轴上表示解集:
解:(1)去括号,得 .
移项,得 .
合并同类项,得 .
系数化为1,得 .
新课讲解
0
这个不等式的解集在数轴上的表示如图所示:
新课讲解
解:(2)去分母,得 ,
去括号,得 ,
移项,得 ,
合并同类项,得 ,
系数化为1,得 .
这个不等式的解集在数轴上的表示如图所示:
0
8
新课讲解
特别注意,当不等式的两边都乘(或除以)同一个负数时,不等号的方向改变.
归纳:解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
新课讲解
①3x-1≥4; ② ③ ④
1.下列式子中,一元一次不等式有( ).
⑤
⑥
⑦
⑧
A.5个 B.4个 C.6个 D.3个
C
巩固练习
2.解下列不等式,并在数轴上表示不等式的解集.
(1)5x+15>4x-1;
(2)2(x+5)≤3(x-5);
(4) .
(3) ;
巩固练习
解:(1)移项,得5x-4x>-1-15.
合并同类项,得x>-16.
这个不等式的解集在数轴上的表示如图所示:
巩固练习
(2)去括号,得2x+10≤3x-15.
移项,得2x-3x≤-15-10.
合并同类项,得-x≤-25.
系数化为1,得x≥25.
这个不等式的解集在数轴上的表示如图所示:
巩固练习
(3)去分母,得
去括号,得
移项,得
合并同类项,得
这个不等式的解集在数轴上表示如图所示:
巩固练习
(4)去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
这个不等式的解集在数轴上表示如图所示:
巩固练习
1.一元一次不等式的定义:含有一个未知数,并且未知数的次数是1的不等式叫做一元一次不等式.
2.解一元一次不等式的步骤:
去分母、去括号、移项、合并同类项、将系数化为1.
要特别注意,当不等式的两边都乘(或除以)同一个负数时,不等号的方向改变.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪
教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
