23.2中心对称 课件
图片预览








文档简介
课件42张PPT。23.2 中心对称观察下面的图形,你有什么发现?一、复习提问:1.什么是轴对称呢?2.关于轴对称的两个图形有哪些性质? 把一个图形沿着某一条直线折叠能与另一个图形完全重合,那么就说这两个图形关于这条直线对称或轴对称.1.两个图形是全等形.
2.对称轴是对称点连线的垂直平分线.3.图形的旋转:
在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形变换称为图形的旋转,这个定点称为旋转中心,旋转的角度称为旋转角.
4.图形的旋转的性质:
①、旋转前后的图形全等.
②、对应点到旋转中心的距离相等.
③、对应点与旋转中心所连线段的夹角等于旋转角.
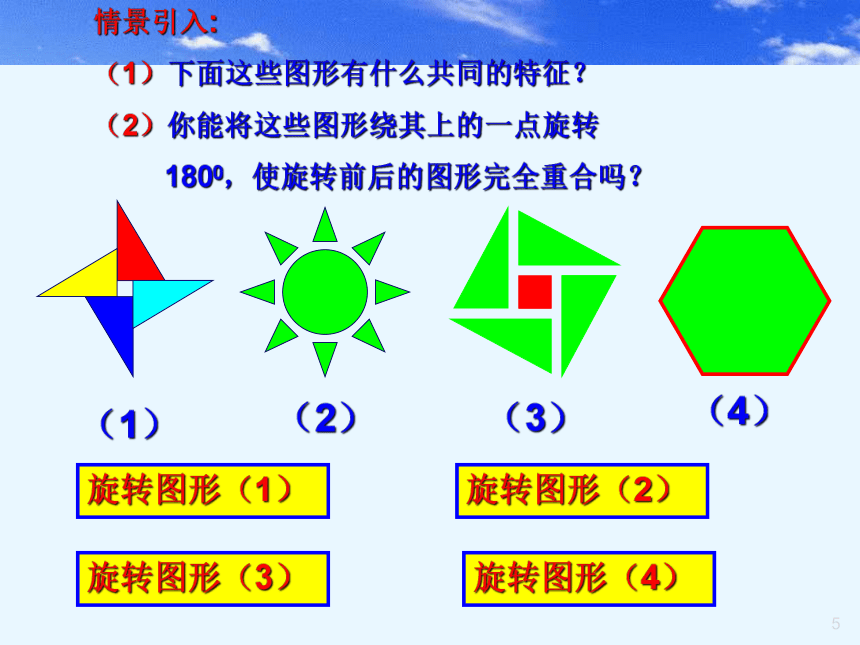
(1)(2)(3)(4)旋转图形(1)旋转图形(2)旋转图形(3)旋转图形(4)情景引入:
(1)下面这些图形有什么共同的特征?
(2)你能将这些图形绕其上的一点旋转
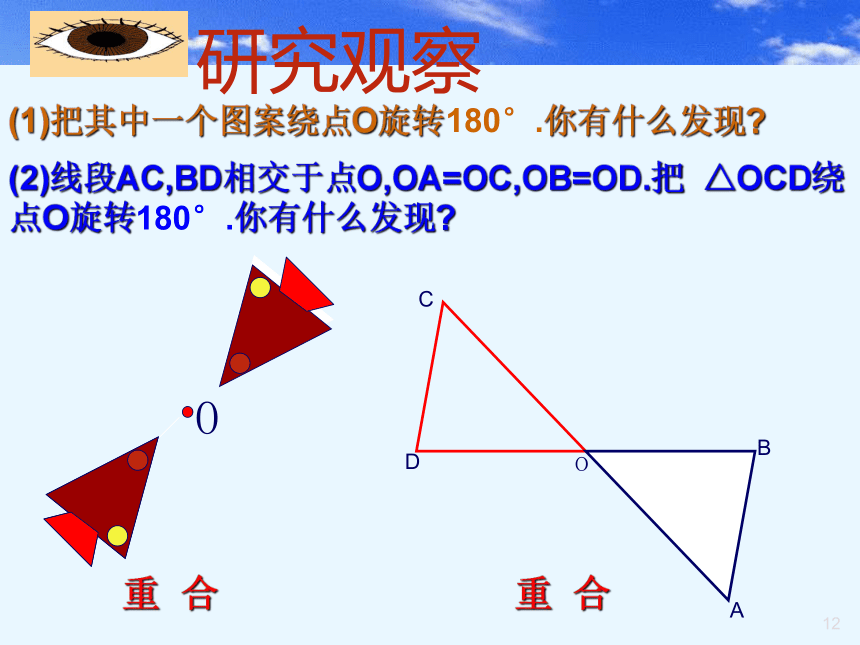
1800,使旋转前后的图形完全重合吗?返回 重 复返回 重 复返回 旋 转返回 旋 转返回 旋 转返回 旋 转(1)把其中一个图案绕点O旋转180°.你有什么发现?
重 合重 合(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°.你有什么发现? OAODBC 像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.观察:C、A、E三点的位置关系怎样?线段AC、AE的大小关系呢?ACB C、A、E三点在一条直线上或∠CAE= 180°. AC=AE1.中心对称的定义:旋转三角板,画关于点O对称的两个三角形:第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;O第三步,移开三角板.合作探究:合作探究:旋转三角板,画关于点O对称的两个三角形:分别连接AA’ ,BB’,CC’。
点O在线段AA′上吗?
如果在,在什么位置? △ABC与△A′B′C′有什么关系?
(1)点O是线段AA ′的中点
(为什?) (2)△ABC≌△A′B′C′
(为什么?)第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;很显然画出的△ABC与△A’B’C’关于点O对称.第三步,移开三角板.(1). 点A′是绕点A旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA′,所以点O在线段AA′上,且OA= OA′,即点O是线段AA′的中点. 同样地,点O是线段BB′ CC′的中点. (2).在△AOB与△ A′ O B′中
OA=OA ′,OB=OB ′ ∠AOB= ∠AOB ′
∴ △AOB≌△ A′ O B′(SAS)
∴AB=A ′ B ′
同理 : BC=B ′ C ′,AC=A ′ C ′
∴ △ABC≌△ A′ B′C ′(SSS)证明:下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?(1)OA=OA′、OB=OB′、 OC=OC′(2)△ABC≌△A′B′C′找一找:(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分.(2)关于中心对称的两个图形是全等形。
2.归纳:中心对称的性质想一想 3.中心对称与轴对称有什么区别?又有什么联系?类比你能得到什么结论?4.中心对称的作图AOA'连结OA,并延长到A',使OA'=OA,例1、(1)已知A点和O点,画出点A关于点O的对称点A'则A'是所求的点例1.(2)、已知线段AB和O点,画出线段AB关于点O的对称线段A' B' OA'B'AB连结AO并延长到A',使OA'=OA,
则得A的对称点A'
连结BO并延长到B' ,使O B' =OB,
则得B的对称点B'连结 A' B' ,则线段A' B'是所画线段例1 (3).如图.选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.解:A′C′B′△A′B′C′即为所求的三角形。
怎么办?可以帮帮我吗?
例1(4) 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。ABA′C′B′D′DOC四边形A1B1C1D1即为所求的图形。画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。提高练习EFGMN你知道怎么办吗? 如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。应用
怎么办?可以帮帮我吗?
解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)OO解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
练习P70. 1. 2 在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形变换称作旋转这个定点称为旋转中心所转动的角称为旋转角旋转的定义旋转三要素旋 转 中 心 、 旋 转 方 向 、
旋 转 角 度1、旋转前后的图形全等 2、对应点到旋转中心的距离相等 3、对应点与旋转中心连线的夹角
等于旋转角 旋转的基本性质把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称,也称这两个图形成中心对称这个点叫作对称中心2个图形中的对应点叫做对称点二、中心对称概念
(2)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.(1)关于中心对称的两个图形是全等形;三、中心对称性质
AA′B′BO 2、线段的中心对称线段的作法AOA′1、点的中心对称点的作法以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
点A′即为所求的点四、灵活运用五、轴对称 与中心对称定义、性质对比对:
两个图形是全等形。
对称点连线都过对称中心,
且被对称中心平分。轴 对 称中心对称123翻转后和另一个图形重合旋转后和另一个图形重合(2)圆(4) 正方形(1)线段(3)平行四边形AB观 察 将下面的图形绕O点旋转180°,你有什么发现?O这些图形是中心对称图形的有( )
——————————————————⑹⑺⑽⑶⑴⑸⑼⑿练一练 这些图形中既是中心对称图形又是轴对称图形的是__________.B、D1.BC
2.对称轴是对称点连线的垂直平分线.3.图形的旋转:
在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形变换称为图形的旋转,这个定点称为旋转中心,旋转的角度称为旋转角.
4.图形的旋转的性质:
①、旋转前后的图形全等.
②、对应点到旋转中心的距离相等.
③、对应点与旋转中心所连线段的夹角等于旋转角.
(1)(2)(3)(4)旋转图形(1)旋转图形(2)旋转图形(3)旋转图形(4)情景引入:
(1)下面这些图形有什么共同的特征?
(2)你能将这些图形绕其上的一点旋转
1800,使旋转前后的图形完全重合吗?返回 重 复返回 重 复返回 旋 转返回 旋 转返回 旋 转返回 旋 转(1)把其中一个图案绕点O旋转180°.你有什么发现?
重 合重 合(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°.你有什么发现? OAODBC 像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.观察:C、A、E三点的位置关系怎样?线段AC、AE的大小关系呢?ACB C、A、E三点在一条直线上或∠CAE= 180°. AC=AE1.中心对称的定义:旋转三角板,画关于点O对称的两个三角形:第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;O第三步,移开三角板.合作探究:合作探究:旋转三角板,画关于点O对称的两个三角形:分别连接AA’ ,BB’,CC’。
点O在线段AA′上吗?
如果在,在什么位置? △ABC与△A′B′C′有什么关系?
(1)点O是线段AA ′的中点
(为什?) (2)△ABC≌△A′B′C′
(为什么?)第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;很显然画出的△ABC与△A’B’C’关于点O对称.第三步,移开三角板.(1). 点A′是绕点A旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA′,所以点O在线段AA′上,且OA= OA′,即点O是线段AA′的中点. 同样地,点O是线段BB′ CC′的中点. (2).在△AOB与△ A′ O B′中
OA=OA ′,OB=OB ′ ∠AOB= ∠AOB ′
∴ △AOB≌△ A′ O B′(SAS)
∴AB=A ′ B ′
同理 : BC=B ′ C ′,AC=A ′ C ′
∴ △ABC≌△ A′ B′C ′(SSS)证明:下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?(1)OA=OA′、OB=OB′、 OC=OC′(2)△ABC≌△A′B′C′找一找:(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分.(2)关于中心对称的两个图形是全等形。
2.归纳:中心对称的性质想一想 3.中心对称与轴对称有什么区别?又有什么联系?类比你能得到什么结论?4.中心对称的作图AOA'连结OA,并延长到A',使OA'=OA,例1、(1)已知A点和O点,画出点A关于点O的对称点A'则A'是所求的点例1.(2)、已知线段AB和O点,画出线段AB关于点O的对称线段A' B' OA'B'AB连结AO并延长到A',使OA'=OA,
则得A的对称点A'
连结BO并延长到B' ,使O B' =OB,
则得B的对称点B'连结 A' B' ,则线段A' B'是所画线段例1 (3).如图.选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.解:A′C′B′△A′B′C′即为所求的三角形。
怎么办?可以帮帮我吗?
例1(4) 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。ABA′C′B′D′DOC四边形A1B1C1D1即为所求的图形。画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。提高练习EFGMN你知道怎么办吗? 如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。应用
怎么办?可以帮帮我吗?
解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)OO解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
练习P70. 1. 2 在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形变换称作旋转这个定点称为旋转中心所转动的角称为旋转角旋转的定义旋转三要素旋 转 中 心 、 旋 转 方 向 、
旋 转 角 度1、旋转前后的图形全等 2、对应点到旋转中心的距离相等 3、对应点与旋转中心连线的夹角
等于旋转角 旋转的基本性质把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称,也称这两个图形成中心对称这个点叫作对称中心2个图形中的对应点叫做对称点二、中心对称概念
(2)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.(1)关于中心对称的两个图形是全等形;三、中心对称性质
AA′B′BO 2、线段的中心对称线段的作法AOA′1、点的中心对称点的作法以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
点A′即为所求的点四、灵活运用五、轴对称 与中心对称定义、性质对比对:
两个图形是全等形。
对称点连线都过对称中心,
且被对称中心平分。轴 对 称中心对称123翻转后和另一个图形重合旋转后和另一个图形重合(2)圆(4) 正方形(1)线段(3)平行四边形AB观 察 将下面的图形绕O点旋转180°,你有什么发现?O这些图形是中心对称图形的有( )
——————————————————⑹⑺⑽⑶⑴⑸⑼⑿练一练 这些图形中既是中心对称图形又是轴对称图形的是__________.B、D1.BC
同课章节目录
