对辅助圆的思考及探究教案(无答案)
图片预览



文档简介
对辅助圆的思考及探究
在几何证明中,困难的并不在于题目,而在于辅助线.在初二学习全等系列的知识点过程中,我们带着学生学习了很多种的辅助线,比如倍长中线、截长补短等.而在学习完圆之后,我们又遇到了新的问题,如做弦的垂线,连接半径,连接直径等.这些的辅助线对于中档的学生都是可以解决的,但我们有没有遇到作出一个圆的辅助线?这也是今天要讲的专题—辅助圆.
“辅助圆”通常活跃于各校模拟试题,因难度系数大,学生不易接受,所以得分率一直都很低.因其考点新颖,有创新又不失难度,所以在近几年的江苏中考中也开始陆续出现了关于“辅助圆”的辅助线问题.
那么下面我就来对“辅助圆”问题说说自己的一些看法.
出现“辅助圆”的情况在我总结来看无外乎就是线段最值、存在唯一点、点的运动等.那下面我就按照如下几点来探究“辅助圆”出现的一般情况.
一 线段最值
线段最值分类相对较多,我们单独来看看什么时候需要我们作出相对的辅助圆的情况.
Ⅰ.折叠中的线段最值
1.(2014年成都中考)如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
2.(2016春?宜兴市校级月考)如图,在Rt△ABC中,∠B=60°,BC=3,D为BC边上的三等分点,BD=2CD,E为AB边上一动点,将△DBE沿DE折叠到△DB′E的位置,连接AB′,则线段AB′的最小值为 .
Ⅱ.圆轨迹中的线段最值
3.(2016年无锡惠山区一模)在平面直角坐标系中,O为坐标原点,以A(4,3)为圆心,1 为半径作圆.P点为圆上一动点,连结OP.点B 为OP 的中点,点C 坐标为(2,0),求BC 的取值范围.
4.(2017 年无锡外国语中学一模)如图,点O在线段AB上,OA=1,OB=3,以O 为圆心,OA 长为半径作圆O.点M 在圆O上运动,连接MB,以MB为腰作等腰Rt△MBC,使∠MBC=90°,M、B、C 三点为逆时针顺序,连接AC,则AC长的取值范围是 .
Ⅲ.直角三角形中的辅助圆
5.( 2017 年江阴校级一模)如图,在等腰直角三角形ABC 中,∠ABC=90°,AB=BC=2,P 是△ABC所在平面内一点,且满足PA⊥PB,则PC的取值范围为 .
6.(2016 年无锡天一中学二模)如图, E,F是正方形ABCD 的边AD上两个动点,满足AE=DF.连接CF 交BD于点G, 连接BE 交AG于点H.若正方形的边长为2,则线段DH 长度的最小值是 .
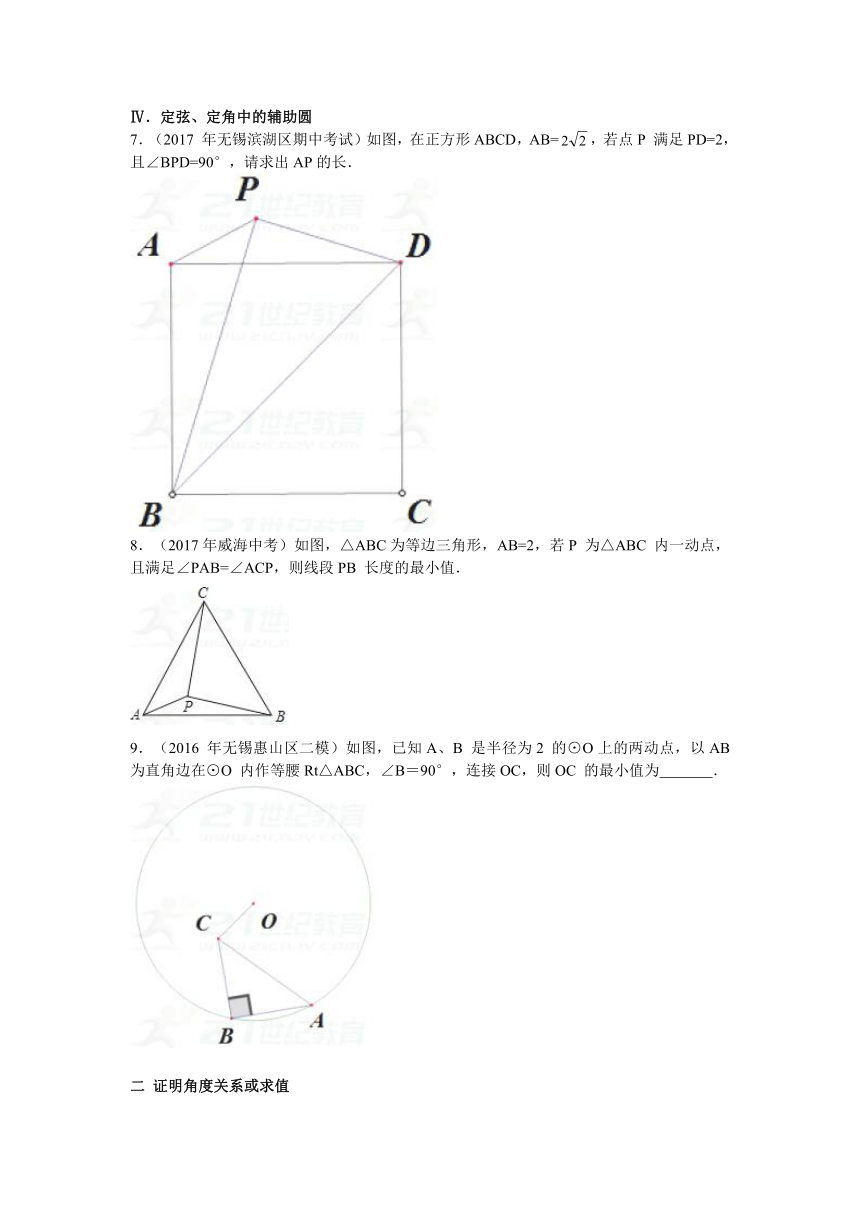
Ⅳ.定弦、定角中的辅助圆
7.(2017 年无锡滨湖区期中考试)如图,在正方形ABCD,AB=,若点P 满足PD=2,且∠BPD=90°,请求出AP的长.
8.(2017年威海中考)如图,△ABC为等边三角形,AB=2,若P 为△ABC 内一动点,且满足∠PAB=∠ACP,则线段PB 长度的最小值.
9.(2016 年无锡惠山区二模)如图,已知A、B 是半径为2 的⊙O上的两动点,以AB为直角边在⊙O 内作等腰Rt△ABC,∠B=90°,连接OC,则OC 的最小值为 .
二 证明角度关系或求值
Ⅰ.角度的倍数关系
1.(2016年月考)如图,AB=AC=AD,如果∠DAC是∠CAB的k倍,那么∠DBC是∠BDC 的( )倍
A.k B.2k C.3k D.不能确定
Ⅱ.角度求值问题
2.( 2015 年无锡惠山区校级月考)已知在正方形ABCD 中,两顶点A、B 分别
在平面直角坐标系的x 轴、y 轴的正半轴上滑动, 点C 点D 在第一象限, 点E
为正方形ABCD 的对称中心, 连结OE, 证明OE 平分角∠ AOB.
Ⅲ.角度最值问题
3.( 2015 年南京市校级月考)如图,O 是半径为2,AB、CD 是互相垂直的两条直径,
点P 是O 上任意一点,过点P 作PM⊥AB 于M, PN⊥CD 于N, 点Q 是MN 的中点,
当点P 沿着圆周从D 运动到点C 时, tan∠QCN 的最大值为 .
三 最值存在问题
Ⅰ.线段范围
1.(2011 年河池中考)如图,在Rt△ABC 中,∠ABC=90°,AB=3,BC=4,P是BC边上的动点.设BP=x,若能在AC 边上找到一点Q,使∠BQP=90°, 则x的取值范围是 .
2.(2015年无锡外国语二模)在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(4,0),点B在第一象限,若N为直线y=-x-2上一点,过B作直线l⊥x轴,在l上是否存在一点M,使得∠OMA=2∠ONA,且这样的点N 有且只有一个.若存在,请直接写出点M的坐标;若不存在,请说明理由.
Ⅱ. 路程长或面积问题
3.(2015 年无锡惠山区校级月考)如图,矩形OABC 的边OA、OC分别在x 轴、y 轴上,点B 的坐标为(7,3),点E 在边AB上,且AE=1,已知点P 为y 轴上一动点,连接EP,过点O 作直线EP 的垂线段,垂足为点H,在点P 从点F(0,)运动到原点O 的过
程中,点H 的运动路径长为 .
4.(2015年无锡外国语月考)如图,圆O的半径为2,弦AB=2,点P为优弧AB上一动点,BC⊥BP交直线PA于点C,则△ABC的最大面积为 .
在几何证明中,困难的并不在于题目,而在于辅助线.在初二学习全等系列的知识点过程中,我们带着学生学习了很多种的辅助线,比如倍长中线、截长补短等.而在学习完圆之后,我们又遇到了新的问题,如做弦的垂线,连接半径,连接直径等.这些的辅助线对于中档的学生都是可以解决的,但我们有没有遇到作出一个圆的辅助线?这也是今天要讲的专题—辅助圆.
“辅助圆”通常活跃于各校模拟试题,因难度系数大,学生不易接受,所以得分率一直都很低.因其考点新颖,有创新又不失难度,所以在近几年的江苏中考中也开始陆续出现了关于“辅助圆”的辅助线问题.
那么下面我就来对“辅助圆”问题说说自己的一些看法.
出现“辅助圆”的情况在我总结来看无外乎就是线段最值、存在唯一点、点的运动等.那下面我就按照如下几点来探究“辅助圆”出现的一般情况.
一 线段最值
线段最值分类相对较多,我们单独来看看什么时候需要我们作出相对的辅助圆的情况.
Ⅰ.折叠中的线段最值
1.(2014年成都中考)如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
2.(2016春?宜兴市校级月考)如图,在Rt△ABC中,∠B=60°,BC=3,D为BC边上的三等分点,BD=2CD,E为AB边上一动点,将△DBE沿DE折叠到△DB′E的位置,连接AB′,则线段AB′的最小值为 .
Ⅱ.圆轨迹中的线段最值
3.(2016年无锡惠山区一模)在平面直角坐标系中,O为坐标原点,以A(4,3)为圆心,1 为半径作圆.P点为圆上一动点,连结OP.点B 为OP 的中点,点C 坐标为(2,0),求BC 的取值范围.
4.(2017 年无锡外国语中学一模)如图,点O在线段AB上,OA=1,OB=3,以O 为圆心,OA 长为半径作圆O.点M 在圆O上运动,连接MB,以MB为腰作等腰Rt△MBC,使∠MBC=90°,M、B、C 三点为逆时针顺序,连接AC,则AC长的取值范围是 .
Ⅲ.直角三角形中的辅助圆
5.( 2017 年江阴校级一模)如图,在等腰直角三角形ABC 中,∠ABC=90°,AB=BC=2,P 是△ABC所在平面内一点,且满足PA⊥PB,则PC的取值范围为 .
6.(2016 年无锡天一中学二模)如图, E,F是正方形ABCD 的边AD上两个动点,满足AE=DF.连接CF 交BD于点G, 连接BE 交AG于点H.若正方形的边长为2,则线段DH 长度的最小值是 .
Ⅳ.定弦、定角中的辅助圆
7.(2017 年无锡滨湖区期中考试)如图,在正方形ABCD,AB=,若点P 满足PD=2,且∠BPD=90°,请求出AP的长.
8.(2017年威海中考)如图,△ABC为等边三角形,AB=2,若P 为△ABC 内一动点,且满足∠PAB=∠ACP,则线段PB 长度的最小值.
9.(2016 年无锡惠山区二模)如图,已知A、B 是半径为2 的⊙O上的两动点,以AB为直角边在⊙O 内作等腰Rt△ABC,∠B=90°,连接OC,则OC 的最小值为 .
二 证明角度关系或求值
Ⅰ.角度的倍数关系
1.(2016年月考)如图,AB=AC=AD,如果∠DAC是∠CAB的k倍,那么∠DBC是∠BDC 的( )倍
A.k B.2k C.3k D.不能确定
Ⅱ.角度求值问题
2.( 2015 年无锡惠山区校级月考)已知在正方形ABCD 中,两顶点A、B 分别
在平面直角坐标系的x 轴、y 轴的正半轴上滑动, 点C 点D 在第一象限, 点E
为正方形ABCD 的对称中心, 连结OE, 证明OE 平分角∠ AOB.
Ⅲ.角度最值问题
3.( 2015 年南京市校级月考)如图,O 是半径为2,AB、CD 是互相垂直的两条直径,
点P 是O 上任意一点,过点P 作PM⊥AB 于M, PN⊥CD 于N, 点Q 是MN 的中点,
当点P 沿着圆周从D 运动到点C 时, tan∠QCN 的最大值为 .
三 最值存在问题
Ⅰ.线段范围
1.(2011 年河池中考)如图,在Rt△ABC 中,∠ABC=90°,AB=3,BC=4,P是BC边上的动点.设BP=x,若能在AC 边上找到一点Q,使∠BQP=90°, 则x的取值范围是 .
2.(2015年无锡外国语二模)在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(4,0),点B在第一象限,若N为直线y=-x-2上一点,过B作直线l⊥x轴,在l上是否存在一点M,使得∠OMA=2∠ONA,且这样的点N 有且只有一个.若存在,请直接写出点M的坐标;若不存在,请说明理由.
Ⅱ. 路程长或面积问题
3.(2015 年无锡惠山区校级月考)如图,矩形OABC 的边OA、OC分别在x 轴、y 轴上,点B 的坐标为(7,3),点E 在边AB上,且AE=1,已知点P 为y 轴上一动点,连接EP,过点O 作直线EP 的垂线段,垂足为点H,在点P 从点F(0,)运动到原点O 的过
程中,点H 的运动路径长为 .
4.(2015年无锡外国语月考)如图,圆O的半径为2,弦AB=2,点P为优弧AB上一动点,BC⊥BP交直线PA于点C,则△ABC的最大面积为 .
同课章节目录
