人教A版高中数学必修二4.3.空间直角坐标系课件(共45张PPT)
文档属性
| 名称 | 人教A版高中数学必修二4.3.空间直角坐标系课件(共45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 652.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-15 11:05:42 | ||
图片预览




文档简介
课件45张PPT。4.3 空间直角坐标系
4.3.1 空间直角坐标系x0数轴上的点可以用
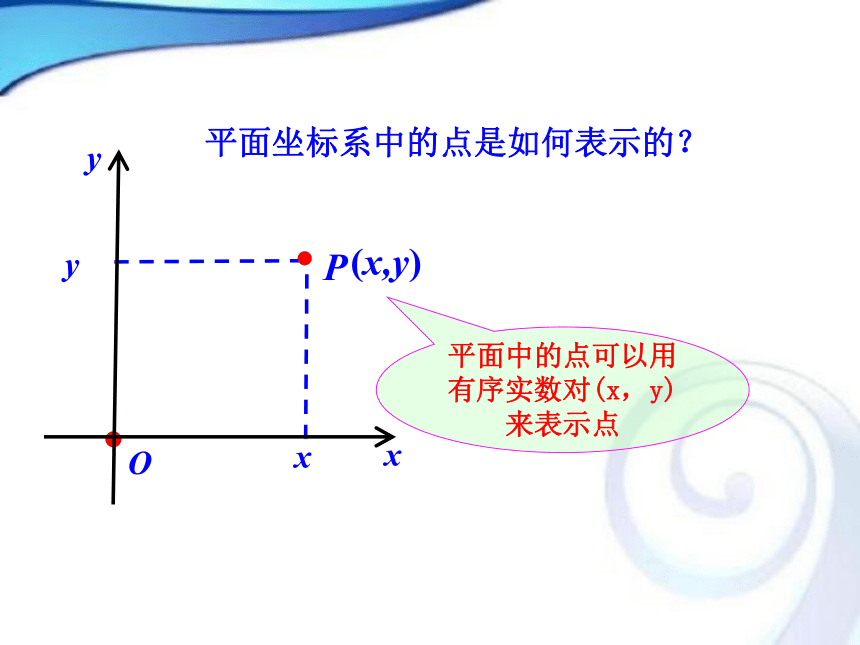
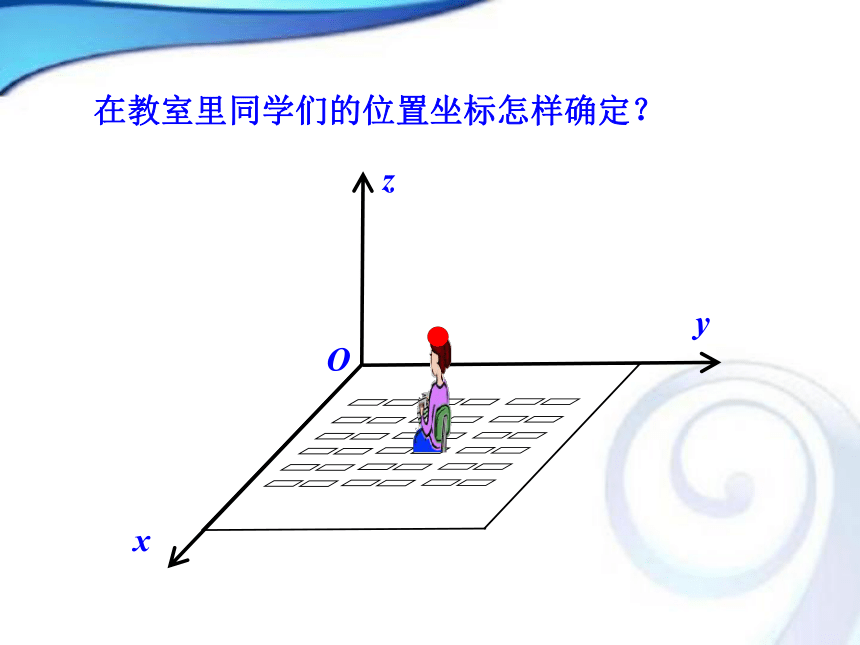
唯一的一个实数表示-1-2123AB数轴上的点是如何表示的?平面中的点可以用有序实数对(x,y)来表示点xyPOxy(x,y)平面坐标系中的点是如何表示的?yOxz在教室里同学们的位置坐标怎样确定?1.空间直角坐标系的建立,空间直角坐标系的划分.
2.空间点的坐标,特殊位置的点的坐标.(重点、难点)
3.空间点的对称问题.
4.掌握空间两点间的距离公式.(重点)
5.会应用距离公式解决有关问题.(难点)
6.通过对空间两点间距离公式的探究与推导,初步
意识到将空间问题转化为平面问题是解决空间
问题的基本思想方法.
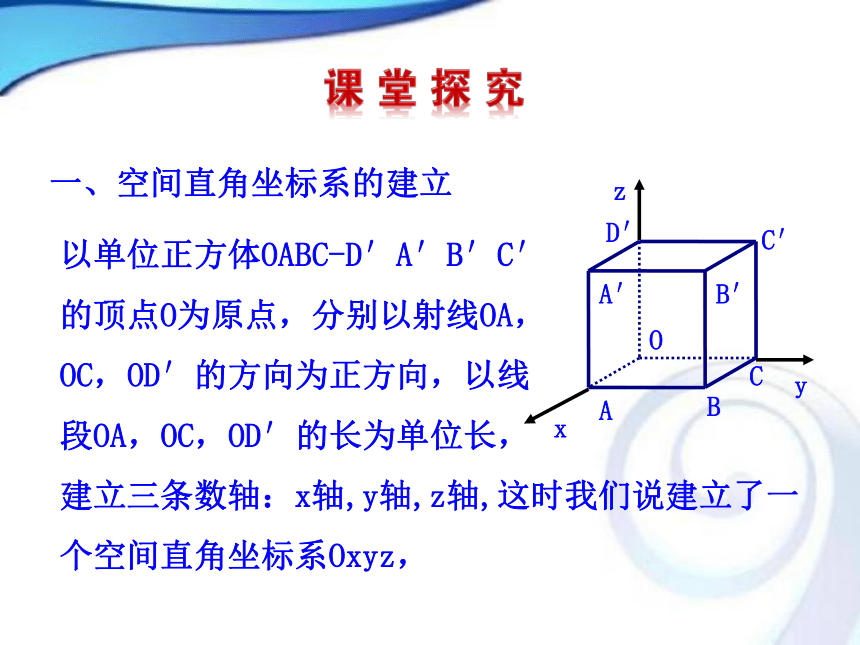
一、空间直角坐标系的建立以单位正方体OABC-D′A′B′C′
的顶点O为原点,分别以射线OA,
OC,OD′的方向为正方向,以线
段OA,OC,OD′的长为单位长,
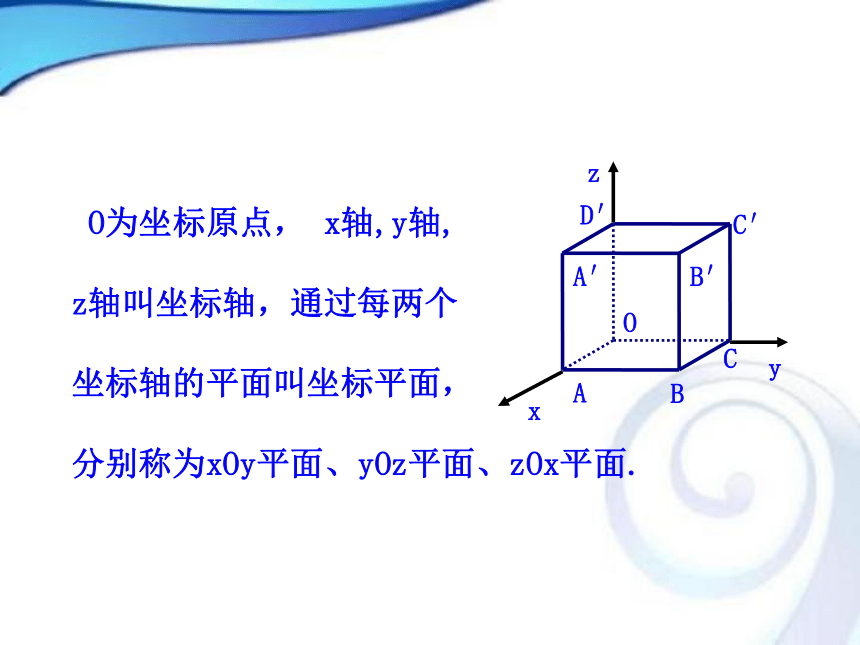
建立三条数轴:x轴,y轴,z轴,这时我们说建立了一个空间直角坐标系Oxyz,B O为坐标原点, x轴,y轴,
z轴叫坐标轴,通过每两个
坐标轴的平面叫坐标平面,
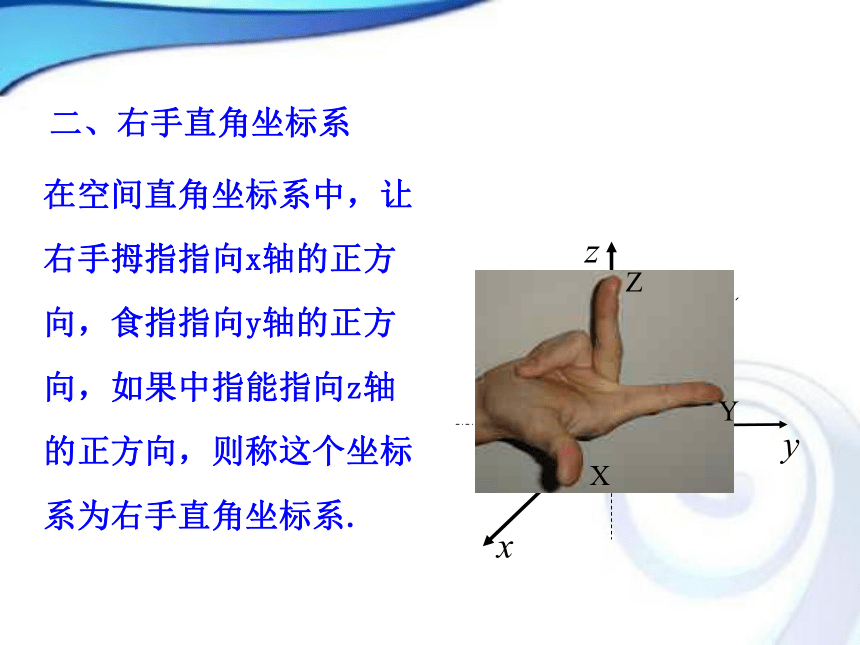
分别称为xOy平面、yOz平面、zOx平面.B二、右手直角坐标系在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指能指向z轴的正方向,则称这个坐标系为右手直角坐标系.o1.x轴与y轴、x轴与z轴均成135°,
而z轴垂直于y轴.2.y轴和z轴的单位长度相同,
x轴上的单位长度为y轴
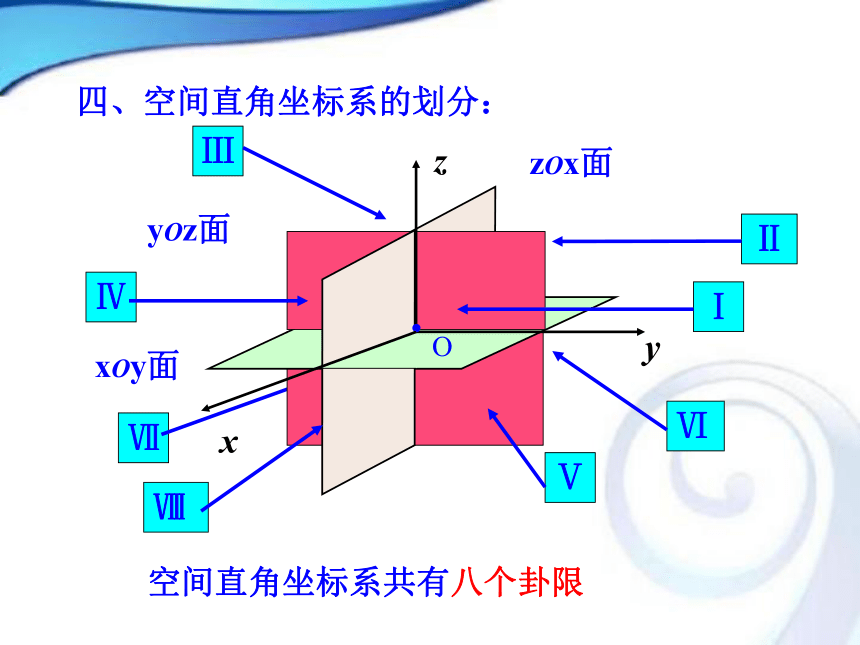
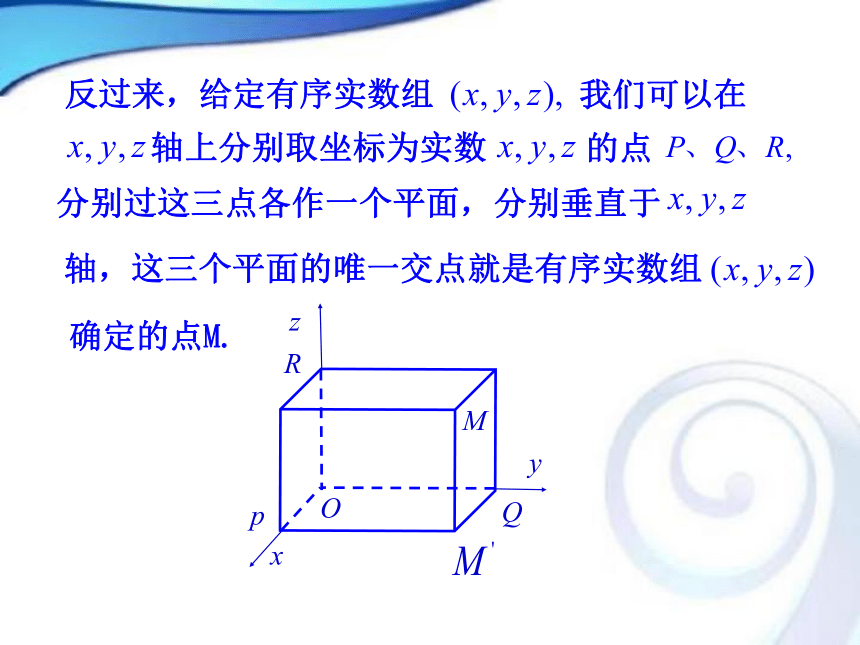
(或z轴)的单位长度的一半.三、空间直角坐标系的画法zOx面xOy面yOz面空间直角坐标系共有八个卦限四、空间直角坐标系的划分:如图所示,设点为空间一定点,过点M分别作垂直于轴的平面,交点依次为设点在轴上的坐标分别为那么点就对应唯一确定的有序实数组五、空间直角坐标系中的坐标.反过来,给定有序实数组我们可以在确定的点M. 轴上分别取坐标为实数的点分别过这三点各作一个平面,分别垂直于轴,这三个平面的唯一交点就是有序实数组这样,空间一点M的坐标可以用有序实数组其中分别叫做点M的横坐标、纵坐标、竖坐标. 来表示,有序实数组叫做点M在空间直角坐标系中的坐标,记作M?PQRyxz??3、空间中点的坐标对于空间任意一点M,要求它的坐标 方法一:过M点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P、Q、R,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值
叫做 P点的横坐标、纵坐标、竖坐标。??P0xyz M点坐标为
(x,y,z)P13、空间中点的坐标 方法二:过M点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足 在z轴上的坐标z就是P点的竖坐标。XYO例如:在空间直角坐标系中,画出下列各点:A(1,2,3), B(2,0,4), C(0,0,3).小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0.六、特殊位置的点的坐标:(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)xOy平面上的点竖坐标为0;yOz平面上的点横坐标为0;xOz平面上的点纵坐标为0.x轴上的点纵坐标和竖坐标都为0;z轴上的点横坐标和纵坐标都为0.y轴上的点横坐标和竖坐标都为0;(1)坐标平面内的点:(2)坐标轴上的点:例1 如图,在长方体OABC-D′A′B′C′中,|OA|=3,|OC|=4,|OD′|=2,写出D′,C,A′,B′四点的坐标.知识应用同理,点A′的坐标是
(3,0,2).解:点D′在z 轴上,且|OD′|=2,它的竖坐标是2;点C在y 轴上,且|OC|=4,它的纵坐标是4;它的横坐标x与纵坐标y都是零,所以点D′的坐标是(0,0,2).它的横坐标x与竖坐标z 都是零,所以点C的坐标是(0,4,0).点B′在xOy平面上的射影是B,因此它的横坐标x与纵坐标y同点B的横坐标x与纵坐标y相同.在xOy平面上,点B横坐标x=3,纵坐标y=4;点B′在z轴上的射影是D′,它的竖坐标与点D′的竖坐标相同,点D′的竖坐标z=2. 所以点B′的坐标是(3,4,2). 如图,在长方体OABC-D′A′B′C′中,|OA|
=3,|OC|=4,|OD′|=3,A′C′与B′D′相交于点P.分别写出点C,B′,P的坐标.答案:【变式练习】例2 结晶体的基本单位称为晶胞,如图(1)是食盐晶胞的示意图(可看成是八个棱长为 的小正方体堆积成的正方体),其中红点代表钠原子,黑点代表氯原子.如图(2),建立空间直角坐标系Oxyz后,试写出全部钠原子所在位置的坐标.(1)(2)解:把图中的钠原子分成下、中、上三层来写它们所在位置的坐标.下层的原子全部在xOy平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位置的坐标分别是 上层的原子所在的平面平行于xOy平面,与z轴
交点的竖坐标为1,所以,这五个钠原子所在位置
的坐标分别是 中层的原子所在的平面平行于xOy平面,与z轴
交点的竖坐标为 ,所以,这四个钠原子所在位置
的坐标分别是一般的P(x,y,z) 关于:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;关于谁对称谁不变求对称点【变式练习】 在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.长a,宽b,高c的长方体的对角线,怎么求?在空间直角坐标系中,点P(x,y,z)到xOy平面的距离,怎么求?一、探究:空间两点间的距离公式垂线段的长 在空间直角坐标系中,点P(x0,y0,z0)到坐标轴的距离,怎么求?垂线段的长1.空间点到原点的距离探究:如果是定长r,那么表示什么图形? 在空间中,到定点的距离
等于定长的点的轨迹是以原点为球心,
半径长为 r 的球面. 2.如果是空间中任意一点P1(x1,y1,z1)到点P2(x2,y2,z2)之间的距离公式会是怎样呢?如图,设P1(x1,y1,z1)、P2(x2,y2,z2)是空间中任意两点,且点P1(x1,y1,z1)、P2(x2,y2,z2)在xOy平面上的射影分别为M,N,那么M,N的坐标为M(x1,y1,0), N(x2,y2,0).在xOy平面上,过点P1作P2N的垂线,垂足为H,则所以因此,空间中任意两点P1(x1,y1,z1)、
P2(x2,y2,z2)之间的距离 在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z):二、空间中点坐标公式原结论成立.证明:例1 求证以M1(4,3,1)、M2(7,1,2)、M3(5,2,3)三点为顶点的三角形是一个等腰三角形.答案:1.求下列两点的距离【变式练习】例2. 在z轴上求与两点A(?4, 1, 7)和B(3, 5, ?2)等距离的点. 解:设所求的点为M(0, 0, z),依题意有 解之得即所以所求点的坐标是答案:在z轴上求一点M,使点M 到A(1,0,2)与点B(1,-3,1)的距离相等.【变式练习】y???ABC?DEF??1.在空间直角坐标系中描出下列各点,并说明这些点的位置 A(0,1,1),B(0,0,2),C(0,2,0),
D(1,0,3),E(2,2,0),F(1,0,0)2.点M(2,-3,1)关于坐标原点的对称点是__ _____ .3.在空间直角坐标系中,若点B是点A(1,2,3)在
坐标平面yOz内的射影,则OB的长度为______.4.以棱长为1的正方体ABCD-A1B1C1D1的棱AB、AD、
AA1所在的直线分别为x,y,z轴,建立空间直角坐标系,则面AA1B1B对角线交点的坐标为_________.(-2,3,-1)5.已知点P在z轴上满足|OP|=1(O是坐标原点),
则点P到点A(1,1,1)的距离是_________.
6.正方体不在同一平面上的两个顶点的坐标分别
为A(-1,2,-1),B(3,-2,3),则正方体的棱长
为_____.41.空间直角坐标系的建立(三步).2.空间直角坐标系的划分(八个卦限).3.空间中点的坐标(一一对应).4.特殊位置的点的坐标(表格).5.空间点的对称问题.类比猜想两点间距离公式
4.3.1 空间直角坐标系x0数轴上的点可以用
唯一的一个实数表示-1-2123AB数轴上的点是如何表示的?平面中的点可以用有序实数对(x,y)来表示点xyPOxy(x,y)平面坐标系中的点是如何表示的?yOxz在教室里同学们的位置坐标怎样确定?1.空间直角坐标系的建立,空间直角坐标系的划分.
2.空间点的坐标,特殊位置的点的坐标.(重点、难点)
3.空间点的对称问题.
4.掌握空间两点间的距离公式.(重点)
5.会应用距离公式解决有关问题.(难点)
6.通过对空间两点间距离公式的探究与推导,初步
意识到将空间问题转化为平面问题是解决空间
问题的基本思想方法.
一、空间直角坐标系的建立以单位正方体OABC-D′A′B′C′
的顶点O为原点,分别以射线OA,
OC,OD′的方向为正方向,以线
段OA,OC,OD′的长为单位长,
建立三条数轴:x轴,y轴,z轴,这时我们说建立了一个空间直角坐标系Oxyz,B O为坐标原点, x轴,y轴,
z轴叫坐标轴,通过每两个
坐标轴的平面叫坐标平面,
分别称为xOy平面、yOz平面、zOx平面.B二、右手直角坐标系在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指能指向z轴的正方向,则称这个坐标系为右手直角坐标系.o1.x轴与y轴、x轴与z轴均成135°,
而z轴垂直于y轴.2.y轴和z轴的单位长度相同,
x轴上的单位长度为y轴
(或z轴)的单位长度的一半.三、空间直角坐标系的画法zOx面xOy面yOz面空间直角坐标系共有八个卦限四、空间直角坐标系的划分:如图所示,设点为空间一定点,过点M分别作垂直于轴的平面,交点依次为设点在轴上的坐标分别为那么点就对应唯一确定的有序实数组五、空间直角坐标系中的坐标.反过来,给定有序实数组我们可以在确定的点M. 轴上分别取坐标为实数的点分别过这三点各作一个平面,分别垂直于轴,这三个平面的唯一交点就是有序实数组这样,空间一点M的坐标可以用有序实数组其中分别叫做点M的横坐标、纵坐标、竖坐标. 来表示,有序实数组叫做点M在空间直角坐标系中的坐标,记作M?PQRyxz??3、空间中点的坐标对于空间任意一点M,要求它的坐标 方法一:过M点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P、Q、R,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值
叫做 P点的横坐标、纵坐标、竖坐标。??P0xyz M点坐标为
(x,y,z)P13、空间中点的坐标 方法二:过M点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足 在z轴上的坐标z就是P点的竖坐标。XYO例如:在空间直角坐标系中,画出下列各点:A(1,2,3), B(2,0,4), C(0,0,3).小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0.六、特殊位置的点的坐标:(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)xOy平面上的点竖坐标为0;yOz平面上的点横坐标为0;xOz平面上的点纵坐标为0.x轴上的点纵坐标和竖坐标都为0;z轴上的点横坐标和纵坐标都为0.y轴上的点横坐标和竖坐标都为0;(1)坐标平面内的点:(2)坐标轴上的点:例1 如图,在长方体OABC-D′A′B′C′中,|OA|=3,|OC|=4,|OD′|=2,写出D′,C,A′,B′四点的坐标.知识应用同理,点A′的坐标是
(3,0,2).解:点D′在z 轴上,且|OD′|=2,它的竖坐标是2;点C在y 轴上,且|OC|=4,它的纵坐标是4;它的横坐标x与纵坐标y都是零,所以点D′的坐标是(0,0,2).它的横坐标x与竖坐标z 都是零,所以点C的坐标是(0,4,0).点B′在xOy平面上的射影是B,因此它的横坐标x与纵坐标y同点B的横坐标x与纵坐标y相同.在xOy平面上,点B横坐标x=3,纵坐标y=4;点B′在z轴上的射影是D′,它的竖坐标与点D′的竖坐标相同,点D′的竖坐标z=2. 所以点B′的坐标是(3,4,2). 如图,在长方体OABC-D′A′B′C′中,|OA|
=3,|OC|=4,|OD′|=3,A′C′与B′D′相交于点P.分别写出点C,B′,P的坐标.答案:【变式练习】例2 结晶体的基本单位称为晶胞,如图(1)是食盐晶胞的示意图(可看成是八个棱长为 的小正方体堆积成的正方体),其中红点代表钠原子,黑点代表氯原子.如图(2),建立空间直角坐标系Oxyz后,试写出全部钠原子所在位置的坐标.(1)(2)解:把图中的钠原子分成下、中、上三层来写它们所在位置的坐标.下层的原子全部在xOy平面上,它们所在位置的竖坐标全是0,所以这五个钠原子所在位置的坐标分别是 上层的原子所在的平面平行于xOy平面,与z轴
交点的竖坐标为1,所以,这五个钠原子所在位置
的坐标分别是 中层的原子所在的平面平行于xOy平面,与z轴
交点的竖坐标为 ,所以,这四个钠原子所在位置
的坐标分别是一般的P(x,y,z) 关于:
(1)x轴对称的点P1为__________;
(2)y轴对称的点P2为__________;
(3)z轴对称的点P3为__________;关于谁对称谁不变求对称点【变式练习】 在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.长a,宽b,高c的长方体的对角线,怎么求?在空间直角坐标系中,点P(x,y,z)到xOy平面的距离,怎么求?一、探究:空间两点间的距离公式垂线段的长 在空间直角坐标系中,点P(x0,y0,z0)到坐标轴的距离,怎么求?垂线段的长1.空间点到原点的距离探究:如果是定长r,那么表示什么图形? 在空间中,到定点的距离
等于定长的点的轨迹是以原点为球心,
半径长为 r 的球面. 2.如果是空间中任意一点P1(x1,y1,z1)到点P2(x2,y2,z2)之间的距离公式会是怎样呢?如图,设P1(x1,y1,z1)、P2(x2,y2,z2)是空间中任意两点,且点P1(x1,y1,z1)、P2(x2,y2,z2)在xOy平面上的射影分别为M,N,那么M,N的坐标为M(x1,y1,0), N(x2,y2,0).在xOy平面上,过点P1作P2N的垂线,垂足为H,则所以因此,空间中任意两点P1(x1,y1,z1)、
P2(x2,y2,z2)之间的距离 在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z):二、空间中点坐标公式原结论成立.证明:例1 求证以M1(4,3,1)、M2(7,1,2)、M3(5,2,3)三点为顶点的三角形是一个等腰三角形.答案:1.求下列两点的距离【变式练习】例2. 在z轴上求与两点A(?4, 1, 7)和B(3, 5, ?2)等距离的点. 解:设所求的点为M(0, 0, z),依题意有 解之得即所以所求点的坐标是答案:在z轴上求一点M,使点M 到A(1,0,2)与点B(1,-3,1)的距离相等.【变式练习】y???ABC?DEF??1.在空间直角坐标系中描出下列各点,并说明这些点的位置 A(0,1,1),B(0,0,2),C(0,2,0),
D(1,0,3),E(2,2,0),F(1,0,0)2.点M(2,-3,1)关于坐标原点的对称点是__ _____ .3.在空间直角坐标系中,若点B是点A(1,2,3)在
坐标平面yOz内的射影,则OB的长度为______.4.以棱长为1的正方体ABCD-A1B1C1D1的棱AB、AD、
AA1所在的直线分别为x,y,z轴,建立空间直角坐标系,则面AA1B1B对角线交点的坐标为_________.(-2,3,-1)5.已知点P在z轴上满足|OP|=1(O是坐标原点),
则点P到点A(1,1,1)的距离是_________.
6.正方体不在同一平面上的两个顶点的坐标分别
为A(-1,2,-1),B(3,-2,3),则正方体的棱长
为_____.41.空间直角坐标系的建立(三步).2.空间直角坐标系的划分(八个卦限).3.空间中点的坐标(一一对应).4.特殊位置的点的坐标(表格).5.空间点的对称问题.类比猜想两点间距离公式
