2018年陕西中考——数学备考课件(165张PPT)
文档属性
| 名称 | 2018年陕西中考——数学备考课件(165张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 11.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-18 00:00:00 | ||
图片预览










文档简介
课件170张PPT。陕西数学中考
之分析和备考陕西数学中考
之分析和备考
2016、2017陕西中考特点1.考试要求发生变化(课标变化)
(双基到四基,两能到四能)
2.试卷结构发生变化(理念变化)
3.比例分值发生变化(课时变化)
10×3分=30分——选择
4×3分=12分——填空
(15+16+17+18)×5分=20分——解答
(19+20+21+22)×7分=28分——解答
23×8分+24×10分+25×12分=20分
各年份数学试题
及成因第1题
各年份数学试题
及成因第1题有理数的学习
3、为什么对“加、减、乘、除”要再学习2、绝对值的两个定义的拓展1、负数的数学史和我们现实的联系4、运算律为什么只在加法乘法中有?5、三级运算的运算顺序6、科学计数法——阅读与思考 长度的测量
中考数学试题
考点和题位第1题选择题 第1题:
考点:四大概念——倒数、绝对值、相反数、数轴、
幂运算(新秀)
成因:数系的第一次扩充——加入了负数(意义)
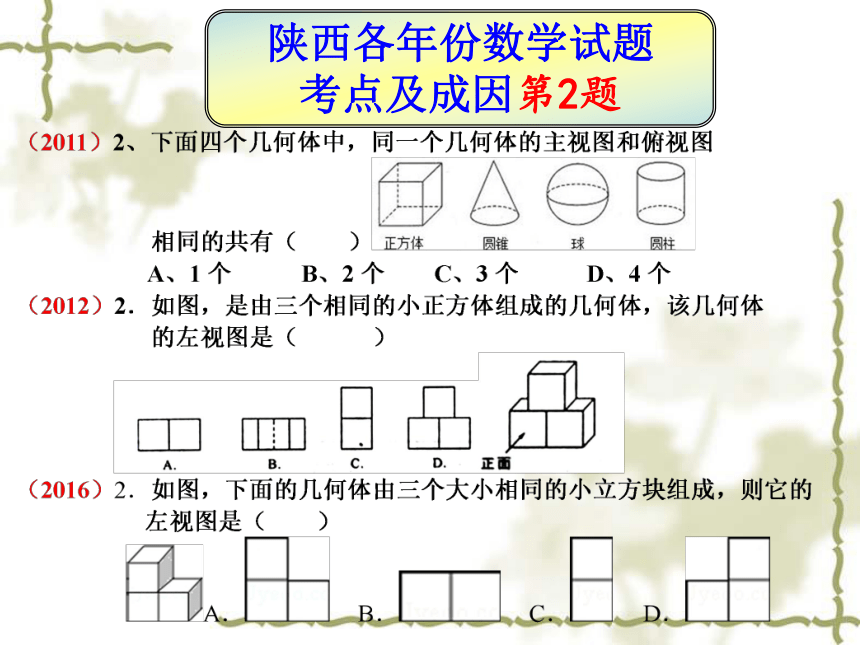
陕西各年份数学试题
考点及成因第2题
陕西各年份数学试题
考点及成因第2题
陕西各年份数学试题
考点及成因第2题生活中的几何体
3、几何体承载的数学思想2、了解几何体的几个特征量
1、现实生活中的三视图4、几何体展开图的拓展和一重要题型选择题 第2题:
考点:简单几何体的组合或切割后的三视图
成因:平面几何的入门知识
中考数学试题
考点和题位第2题
各年份3试题
考点及成因
各年份3试题
考点及成因第一年用分式的加减运算替代幂的四种运算,是升级,强化运算能力的表现 整式的加减
整式的乘除与因式分解
分式
3、整式乘法、十字相乘分解因式、求根公
式分解因式的熟练掌握2、三兄弟1、探索规律——五规律4、两种计算中运算过程程序化5、分式方程中的增根和无解6、数学思想的渗透2011年17题漏乘了!x典型问题答卷得分率低,
如何想办法解决?
让其成为优势!×漏变号了——考题中17题的考法×分母不见了——考题中17题的考法
选择题 第3题:
考点:幂的四种运算、分式四则混合运算、解分式方程
成因:数系扩充后字母体系的生成,
初中学段的重要标志
备考:同底数幂的乘法、同底数幂的除法、
积的乘方、幂的幂运算;解分式方程5坑;
分式四则混合运算4步
中考数学试题
考点和题位第3、16题
各年份数学试题
及成因第4题
各年份数学试题
及成因第4题
各年份数学试题
及成因第4题相交线与平行线
轴对称
3、平行与角分线的组合2、辅助线的出现是必然、而不是天才具
有的想法1、两点之间线段最短问题的升级选择题 第4题:
考点:线与线平行或相交所成的角,以及对顶角、补角、
邻补角、余角、角的概念和计算
成因:初中几何体系的对象为点和线,线与线的位置
关系必考
中考数学试题
考点和题位第4题
各年份数学试题
及成因第5或7题
各年份数学试题
及成因第5或7题
考点:方程和不等式
成因:初中代数的知识体系首先是数、再是代数式、
接下来的是关系式中考数学试题
考点和题位第5或7题不等式与不等式组
3、简单绝对值不等式的解法2、含字母系数的不等式的解法1、利用不等关系求最值的背景
各年份数学试题
及成因第5或7题
各年份数学试题
及成因第7题
各年份数学试题
及成因第7题
各年份数学试题
及成因第8题
各年份数学试题
及成因第7题 平面直角坐标系
一次函数
3、正比例函数的应试技巧2、平面直角坐标系学习什么1、学习平面直角坐标系的生活背景4、一次函数k的求法5、两个一次函数图象的关系和分段函数
各年份数学试题
及成因第6题
各年份数学试题
及成因第6题 三角形
勾股定理
3、角分线2、内角180度的证明:平行、平角1、三边关系应用,不等关系结论的证明4、中线5、高 三角形
勾股定理
7、五个明星三角形6、直角三角形
选择题 第6题:
考点:三角形的边角关系及其特殊线段的概念
——中点(中位线和中线)、角分线、高、
五心等庞大的知识体系(重中之重)
成因:初中图形与几何内容主角中考数学试题
考点和题位第6题
各年份数学试题
及成因第8题
各年份数学试题
及成因第8题
各年份数学试题
及成因第8题 四边形
2、矩形的折叠1、平行四边形:3、菱形的判定4、正方形为载体的全等
中考数学试题
考点和题位第9题信息(2014)23.如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6.过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A 作切线BD的垂线,垂足为C.
(1)求证:AD平 分∠BAC;
(2)求AC的长.中考数学试题
考点第23题中考数学试题
考点第23题 中考数学试题
考点第23题
中考数学试题
考点第23题解答题 第23题:
考点:圆与直线的位置关系、渗透全等、相似
锐角三角函数、切线定理
考法:不超过3条直线、不超过一个圆
备考:1、圆的切线证明或性质应用
2、相似、勾股定理、解三角求边长
3、三角形或四边形的判定
旋转
圆
相似
3、切线2、圆中角度隐性的决定因素1、垂径定理——方程思想4、相似的模型:
各年份数学试题
及成因第10题
各年份数学试题
及成因第10题
各年份数学试题
及成因第10题 一元一次方程
二元一次方程组
一元二次方程
二次函数
4、比较y值得大小3、给定二次函数图象确定a、b、c关系2、四点串联二次函数基本性质5、函数图象的平移、对称变换对应解析式的变化1、求解析式(2016)24.如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+5经过点M(1,3)和N(3,5)
(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
各年份数学试题
及成因第24题(2017)在同一直角坐标系中,抛物线C1:y=ax2﹣2x﹣3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧
(1)求抛物线C1,C2的函数表达式;
(2)求A、B两点的坐标;
(3)在抛物线C1上是否存在一点P,
在抛物线C2上是否存在一点Q,
使得以AB为边,且以A、B、P、Q
四点为顶点的四边形是平行四边形?
若存在,求出P、Q两点的坐标;若不存在,请说明理由.
各年份数学试题
及成因第24题二次函数
3、几何图形为载体的
分类思想2、图形变换为纽带;
1、方程思想求解析式;待定系数法求解析式图象上的动点问题。根据已知点与动点为顶点构造特殊图形面积,确定符合条件的点的坐标。中考数学试题
备考内容第24题中考数学试题
备考内容第24题中考数学试题
备考内容第24题中考数学试题
备考内容第24题中考数学试题
备考内容第24题中考数学试题
备考内容第24题
各年份数学试题
及成因第11题
各年份数学试题
及成因第15题
选择题 第11题:
考点:无理数推后;转化为解简单不等式或因式分解
成因:初中数系的第二次扩充,标志性的数必考
考法:数感(比较大小)、化简中考数学试题
考点和题位第11题二次根式
3、开偶次、开奇次代表,拓展分数指数2、被开方数为100内整数的熟练程度1、数感的培养
各年份数学试题
成因第12题
各年份数学试题
成因第12题
选择题 第12题:
考点:正多边形、图形的两种变换、测量估算
成因:新课标新增必须体现,学生动手能你弱中考数学试题
考点和题位第12题各年份数学试题
及成因第13题各年份数学试题
及成因第13题各年份数学试题
及成因第13题 反比例函数3、几何定义2、增减性1、反比例函数的对称性4、反比例 函数
与一次函数的关系
2015数学试题
每题考点及成因第12题填空题 第13题:
考点:反比例函数的对称性
增减性
几何定义
反比例 函数与一次函数的关系中考数学试题
考点和题位第13题① (14陕西16)如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上两个动点,且在直线的异侧,若∠AMB=45°,则四边形MANB面积的最大值是________.②(13陕西16)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为 .③(15陕西14)如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M、N分别是AB、BC的中点,则MN长的最大值是 各年份数学试题
及成因第14题
中考数学试题
考点和题位第14题 知识点源于“两点之间线段最短 ”“点到直线的距离中垂线段最短”,更方便的理解“三角形任意两边之和大于第三边,两边之差小于第三边 ”;历史名题“将军饮马”问题。经过了不断的演变,以其极其丰富的表情展现于考生面前!中考数学试题
备考14、25题“将军饮马” 问题
(1)河的宽度忽略不计
(2)河的宽度不能够忽略
中考数学试题
备考第14或25题“将军饮马” 问题
(3)在河岸上建景观带
(4)线段差绝对值的最大值
中考数学试题
备考第14或25题ADCB(5)增加了一条“河”
A是锐角MON内部任意一点,在∠MON的两边OM,
ON上各取一点B、C组成三角形,使三角形周长最小。 (6)增加了一条河和一个点
AB是锐角MON内部一条线段,在角MON的两边OM,
ON上各取一点C,D组成四边形,使四边形周长最小。 2017数学试题
备考第14或25题2.点与线上各点的连线中垂线最短
3.圆中最值2017数学试题
备考第14或25题2017数学试题
备考第14或25题4.几何体中的最值(09)16.如图,在锐角 中, , 的平分线交 于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值 .规律思考B′M′N′中考数学试题
每题考点及成因第14或25题中考数学试题
备考第14或25题考题回顾·方案一:供水站建在点M处,请你求出铺设到甲村某处和
乙村某处的管道长度之和的最小值; 考题回顾M′方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设
到A处,请你在图①中,画出铺设到点A和点M处的管道长度之
和最小的线路图,并求其最小值;考题回顾M′ 方案三:供水站建在甲村(线段AB某处),请你在图中画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值.
(14)25.问题探究
(1)如图①,在矩形ABCD中,AB=3,BC=4.如果BC边上存在点P,使△APD为等腰三角形,那么请画出满足条件的一个等腰△APD,并求出此时BP的长;(2)如图②,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为边AB、AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长;问题解决
(3)有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB.现在要使∠AMB大约为60°,就可以让监控装置的效果达到最佳.已知∠A=∠E=∠D=90°,AB=270m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长;若不存在,请说明理由.2017年陕西25已知抛物线 ,经过点A(4,0),设点
C(1,-3),请在抛物线的对称轴上确定一点D,使|AD-CD|
的值最大,请直接写出点D的坐标。中考数学试题
备考第14或25题已知抛物线 ,经过点A(4,0),设点
C(1,-3),请在抛物线的对称轴上确定一点D,使|AD-CD|
的值最大,请直接写出点D的坐标。中考数学试题
备考第14或25题27.已知抛物线y=ax 2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与x轴平行,O为坐标原点.
(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明
理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax 2+bx+c上的
动点,当△PDO的周长最小时,求四边形CODP的面积. 中考数学试题
备考第14或25题各年份数学试题
第17题 五种基本作图:
1、作一条线段等于已知线段;
2、作一个角等于已知角;
3、作已知线段的垂直平分线;
4、作已知角的角平分线;
5、过一点作已知直线的垂线; 课标要求的尺规作图:
1、过已知直线外一点作已知直线的平行线;
2、会利用基本作图作三角形:(SSS、SAS、ASA、HL、底边及底边上的高作等腰三角形);
3、会利用基本作图完成:作三角形的外接圆、内切圆;作圆的内接正方形和正六边形.中考数学试题
第17题考法和备考 三数、三差:
1、刻画数据整体水平;
2、刻画数据均衡水平、稳定程度;
三种统计图:
1、扇形
2、折线
3、条形(新增:频数分布直方图)通过统计表和统计图分析,做出判断与决策题;
(平均数、中位数、众数的考查在此体现)预估2017数学试题
第18题考法和备考18题——统计:主要考查学生的数据分析观念18题——统计:主要考查学生的数据分析观念 (2016年)某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是 ;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
18题——统计:主要考查学生的数据分析观念 (2017年)某养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A、B、C、D四组,如下表所示,同时,将调查结果绘制成下面两幅不完整的统计图.
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布直方图和扇形统计图;
(2)所抽取的七年级学生早锻炼时间的中位数落在 区间内;
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼) 数据的收集、整理与描述
数据的分析
1、理清楚统计的过程:收集数据、整理
数据、分析数据
各年份数学试题
及成因第19题
各年份数学试题
及成因第19题
各年份数学试题
及成因第19题全等三角形3、三角形中线、角分线为背景的全等2、等腰三角形、等边三角形、正方形
为载体的全等1、全等变换下的全等模型考查内容:主要考查全等三角形的证明及利
用全等 后的性质进行证明或简
单计算等关注:以四边形为载体的三角形全等类问题
相关联三角形的全等类问题中考数学试题
第19题考法和备考 20.①(2012陕西20)如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东 45°方向(点A、B、C在同一水平面上).
请你利用小明测得的相关数据,求
湖心岛上的迎宾槐C处与湖岸
上的凉亭A处之间的距离.各年份数学试题
及成因第20题 20.①(2012陕西20)如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东 45°方向(点A、B、C在同一水平面上).
请你利用小明测得的相关数据,求
湖心岛上的迎宾槐C处与湖岸
上的凉亭A处之间的距离.各年份数学试题
及成因第20题20.②(2014陕西20)某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,……
①小明在B点使视线通过帽檐正好落在树的底部点D处,这时小亮测得小明眼睛距地面的距离AB=1.7米;②小明站在原地转动180°后蹲下,这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,求出河宽BD是多少米?
各年份数学试题
及成因第20题
各年份数学试题
及成因第20题 锐角三角函数
投影与视图
2、双直角三角形模型或两对双直角模型1、公式的变形
中考数学试题第20题
备考1、以测量为载体:考察求线段长度
2、知识载体
3、数学本质:方程思想①(2013陕西21)“五一节”期间,申老师一家自架游去了离家170千米的某地.下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求他们出发半小时时,离家多少千米?
(2)求出AB段图象的函数表达式;
(3)他们出发2小时时,
离目的地还有多少千米?各年份数学试题
及成因第21题②(2014陕西21)小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1kg收费22元,超过1kg,则超出部分按每千克10元加收费用.设该公司从西安到南昌快寄樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5kg樱桃,请你求出这次快寄的费用是多少元?
各年份数学试题
及成因第21题
各年份数学试题
及成因第21题
各年份数学试题
及成因第21题
各年份数学试题
及成因第21题考查内容:利用一次函数模型解决问题的能
力(关系式是桥梁)关注:现实背景分段函数类问题
一次函数与不等式的结合
中考数学试题
第21题考法和备考
解答题 第22题:
考点:摸球事件、转盘游戏、纸牌游戏
考法:不超过6、放回、不放回
中考数学试题
第22题考法和备考字母符合、图形语言、表格、文字语言的结合使用孩子的认真,
让人心疼!平均分5.5 满分率59%
2017数学试题
备考内容第25题25题等分—公平问题1、中心对称图形等分面积2、非中心对称类图形等分面积25题等分—公平问题直线过定点等分面积类问题EFD直线过定点等分面积类问题EEMEFM25题—公平问题25题等分—公平问题(6,0)(2,0)(6,4)(2,4)(4,2)25题等分—公平问题 QEGQF25题等分—面积最值类问题分析:面积均为两个因数积的模式思路一:固定一个因数,另外一个因数的大小决定积的 大小思路二:两个因数均为变量,考虑利用完全平方差公式25题等分—面积最值类问题思路三:两个因数用同一个字母表示,出现该字母的二次模式,
利用二次函数求最值25题—面积最值问题ABCDGFHOECCABAEFNPDENMFPHB(2012陕西25)如图,正三角形ABC的边长为 .
(1)如图①,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上.在正三角形及其内部,以A为位似中心,作正方形EFPN的位似正方形 ,且使正方形 的面积最大(不要求写作法)(2)求(1)中作出的正方形 的边长;
(3)如图②,在正三角形ABC中放入正方形DEMN和正方形EFPM,使得DE、EF在边AB上,点P、N分别在边AC、BC上,求这两个正方形面积和的最大值及最小值,并说明理由. 25题——面积最值问题ABAEFNPDENMFPHBCC设正方形E′F′P′N′的边长为a设两个正方形的面积分别为a和b∴两正方形的面积和为S=a2+b2思路一:两个变量用一个去表示,构造二次函数思路二:两个变量的模式,利用完全平方差公式思路三:利用“三兄弟”关系25题——面积最值问题25题——面积最值问题P25题——面积最值问题
中考数学试题
每题考点及成因第25题解答题 第25题:
考点:以几何图形作为载体,考察抽象、推理、
建模,以三角形、四边形、圆为基本图形
考法:充分应用几何演绎推理、代数演绎推理、
解析演绎,数学建模等
备考:最值问题(距离、周长、面积)、
等分问题
- - - 心中有
全卷 时间
安排 背景
可寻 题图
精准 选择有
规则 应试策略四、应试 你准备好了吗?QQ:450889287Thank you!Your site here欢迎批评指正谢谢!应试—2012选择题答案应试—2013选择题答案应试—2014选择题答案应试—2015选择题答案祝各位老师:
心想事成、工作顺利、身体健康
2017年10月最后让我们怀揣着一种爱走近学生,去关心、了解学生,并不遗余力地尊重他们,懂得维护他们的自尊!
2016、2017陕西中考特点1.考试要求发生变化(课标变化)
(双基到四基,两能到四能)
2.试卷结构发生变化(理念变化)
3.比例分值发生变化(课时变化)
10×3分=30分——选择
4×3分=12分——填空
(15+16+17+18)×5分=20分——解答
(19+20+21+22)×7分=28分——解答
23×8分+24×10分+25×12分=20分
各年份数学试题
及成因第1题
各年份数学试题
及成因第1题有理数的学习
3、为什么对“加、减、乘、除”要再学习2、绝对值的两个定义的拓展1、负数的数学史和我们现实的联系4、运算律为什么只在加法乘法中有?5、三级运算的运算顺序6、科学计数法——阅读与思考 长度的测量
中考数学试题
考点和题位第1题选择题 第1题:
考点:四大概念——倒数、绝对值、相反数、数轴、
幂运算(新秀)
成因:数系的第一次扩充——加入了负数(意义)
陕西各年份数学试题
考点及成因第2题
陕西各年份数学试题
考点及成因第2题
陕西各年份数学试题
考点及成因第2题生活中的几何体
3、几何体承载的数学思想2、了解几何体的几个特征量
1、现实生活中的三视图4、几何体展开图的拓展和一重要题型选择题 第2题:
考点:简单几何体的组合或切割后的三视图
成因:平面几何的入门知识
中考数学试题
考点和题位第2题
各年份3试题
考点及成因
各年份3试题
考点及成因第一年用分式的加减运算替代幂的四种运算,是升级,强化运算能力的表现 整式的加减
整式的乘除与因式分解
分式
3、整式乘法、十字相乘分解因式、求根公
式分解因式的熟练掌握2、三兄弟1、探索规律——五规律4、两种计算中运算过程程序化5、分式方程中的增根和无解6、数学思想的渗透2011年17题漏乘了!x典型问题答卷得分率低,
如何想办法解决?
让其成为优势!×漏变号了——考题中17题的考法×分母不见了——考题中17题的考法
选择题 第3题:
考点:幂的四种运算、分式四则混合运算、解分式方程
成因:数系扩充后字母体系的生成,
初中学段的重要标志
备考:同底数幂的乘法、同底数幂的除法、
积的乘方、幂的幂运算;解分式方程5坑;
分式四则混合运算4步
中考数学试题
考点和题位第3、16题
各年份数学试题
及成因第4题
各年份数学试题
及成因第4题
各年份数学试题
及成因第4题相交线与平行线
轴对称
3、平行与角分线的组合2、辅助线的出现是必然、而不是天才具
有的想法1、两点之间线段最短问题的升级选择题 第4题:
考点:线与线平行或相交所成的角,以及对顶角、补角、
邻补角、余角、角的概念和计算
成因:初中几何体系的对象为点和线,线与线的位置
关系必考
中考数学试题
考点和题位第4题
各年份数学试题
及成因第5或7题
各年份数学试题
及成因第5或7题
考点:方程和不等式
成因:初中代数的知识体系首先是数、再是代数式、
接下来的是关系式中考数学试题
考点和题位第5或7题不等式与不等式组
3、简单绝对值不等式的解法2、含字母系数的不等式的解法1、利用不等关系求最值的背景
各年份数学试题
及成因第5或7题
各年份数学试题
及成因第7题
各年份数学试题
及成因第7题
各年份数学试题
及成因第8题
各年份数学试题
及成因第7题 平面直角坐标系
一次函数
3、正比例函数的应试技巧2、平面直角坐标系学习什么1、学习平面直角坐标系的生活背景4、一次函数k的求法5、两个一次函数图象的关系和分段函数
各年份数学试题
及成因第6题
各年份数学试题
及成因第6题 三角形
勾股定理
3、角分线2、内角180度的证明:平行、平角1、三边关系应用,不等关系结论的证明4、中线5、高 三角形
勾股定理
7、五个明星三角形6、直角三角形
选择题 第6题:
考点:三角形的边角关系及其特殊线段的概念
——中点(中位线和中线)、角分线、高、
五心等庞大的知识体系(重中之重)
成因:初中图形与几何内容主角中考数学试题
考点和题位第6题
各年份数学试题
及成因第8题
各年份数学试题
及成因第8题
各年份数学试题
及成因第8题 四边形
2、矩形的折叠1、平行四边形:3、菱形的判定4、正方形为载体的全等
中考数学试题
考点和题位第9题信息(2014)23.如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6.过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A 作切线BD的垂线,垂足为C.
(1)求证:AD平 分∠BAC;
(2)求AC的长.中考数学试题
考点第23题中考数学试题
考点第23题 中考数学试题
考点第23题
中考数学试题
考点第23题解答题 第23题:
考点:圆与直线的位置关系、渗透全等、相似
锐角三角函数、切线定理
考法:不超过3条直线、不超过一个圆
备考:1、圆的切线证明或性质应用
2、相似、勾股定理、解三角求边长
3、三角形或四边形的判定
旋转
圆
相似
3、切线2、圆中角度隐性的决定因素1、垂径定理——方程思想4、相似的模型:
各年份数学试题
及成因第10题
各年份数学试题
及成因第10题
各年份数学试题
及成因第10题 一元一次方程
二元一次方程组
一元二次方程
二次函数
4、比较y值得大小3、给定二次函数图象确定a、b、c关系2、四点串联二次函数基本性质5、函数图象的平移、对称变换对应解析式的变化1、求解析式(2016)24.如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+5经过点M(1,3)和N(3,5)
(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
各年份数学试题
及成因第24题(2017)在同一直角坐标系中,抛物线C1:y=ax2﹣2x﹣3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧
(1)求抛物线C1,C2的函数表达式;
(2)求A、B两点的坐标;
(3)在抛物线C1上是否存在一点P,
在抛物线C2上是否存在一点Q,
使得以AB为边,且以A、B、P、Q
四点为顶点的四边形是平行四边形?
若存在,求出P、Q两点的坐标;若不存在,请说明理由.
各年份数学试题
及成因第24题二次函数
3、几何图形为载体的
分类思想2、图形变换为纽带;
1、方程思想求解析式;待定系数法求解析式图象上的动点问题。根据已知点与动点为顶点构造特殊图形面积,确定符合条件的点的坐标。中考数学试题
备考内容第24题中考数学试题
备考内容第24题中考数学试题
备考内容第24题中考数学试题
备考内容第24题中考数学试题
备考内容第24题中考数学试题
备考内容第24题
各年份数学试题
及成因第11题
各年份数学试题
及成因第15题
选择题 第11题:
考点:无理数推后;转化为解简单不等式或因式分解
成因:初中数系的第二次扩充,标志性的数必考
考法:数感(比较大小)、化简中考数学试题
考点和题位第11题二次根式
3、开偶次、开奇次代表,拓展分数指数2、被开方数为100内整数的熟练程度1、数感的培养
各年份数学试题
成因第12题
各年份数学试题
成因第12题
选择题 第12题:
考点:正多边形、图形的两种变换、测量估算
成因:新课标新增必须体现,学生动手能你弱中考数学试题
考点和题位第12题各年份数学试题
及成因第13题各年份数学试题
及成因第13题各年份数学试题
及成因第13题 反比例函数3、几何定义2、增减性1、反比例函数的对称性4、反比例 函数
与一次函数的关系
2015数学试题
每题考点及成因第12题填空题 第13题:
考点:反比例函数的对称性
增减性
几何定义
反比例 函数与一次函数的关系中考数学试题
考点和题位第13题① (14陕西16)如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上两个动点,且在直线的异侧,若∠AMB=45°,则四边形MANB面积的最大值是________.②(13陕西16)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为 .③(15陕西14)如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M、N分别是AB、BC的中点,则MN长的最大值是 各年份数学试题
及成因第14题
中考数学试题
考点和题位第14题 知识点源于“两点之间线段最短 ”“点到直线的距离中垂线段最短”,更方便的理解“三角形任意两边之和大于第三边,两边之差小于第三边 ”;历史名题“将军饮马”问题。经过了不断的演变,以其极其丰富的表情展现于考生面前!中考数学试题
备考14、25题“将军饮马” 问题
(1)河的宽度忽略不计
(2)河的宽度不能够忽略
中考数学试题
备考第14或25题“将军饮马” 问题
(3)在河岸上建景观带
(4)线段差绝对值的最大值
中考数学试题
备考第14或25题ADCB(5)增加了一条“河”
A是锐角MON内部任意一点,在∠MON的两边OM,
ON上各取一点B、C组成三角形,使三角形周长最小。 (6)增加了一条河和一个点
AB是锐角MON内部一条线段,在角MON的两边OM,
ON上各取一点C,D组成四边形,使四边形周长最小。 2017数学试题
备考第14或25题2.点与线上各点的连线中垂线最短
3.圆中最值2017数学试题
备考第14或25题2017数学试题
备考第14或25题4.几何体中的最值(09)16.如图,在锐角 中, , 的平分线交 于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值 .规律思考B′M′N′中考数学试题
每题考点及成因第14或25题中考数学试题
备考第14或25题考题回顾·方案一:供水站建在点M处,请你求出铺设到甲村某处和
乙村某处的管道长度之和的最小值; 考题回顾M′方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设
到A处,请你在图①中,画出铺设到点A和点M处的管道长度之
和最小的线路图,并求其最小值;考题回顾M′ 方案三:供水站建在甲村(线段AB某处),请你在图中画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值.
(14)25.问题探究
(1)如图①,在矩形ABCD中,AB=3,BC=4.如果BC边上存在点P,使△APD为等腰三角形,那么请画出满足条件的一个等腰△APD,并求出此时BP的长;(2)如图②,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为边AB、AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长;问题解决
(3)有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB.现在要使∠AMB大约为60°,就可以让监控装置的效果达到最佳.已知∠A=∠E=∠D=90°,AB=270m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长;若不存在,请说明理由.2017年陕西25已知抛物线 ,经过点A(4,0),设点
C(1,-3),请在抛物线的对称轴上确定一点D,使|AD-CD|
的值最大,请直接写出点D的坐标。中考数学试题
备考第14或25题已知抛物线 ,经过点A(4,0),设点
C(1,-3),请在抛物线的对称轴上确定一点D,使|AD-CD|
的值最大,请直接写出点D的坐标。中考数学试题
备考第14或25题27.已知抛物线y=ax 2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与x轴平行,O为坐标原点.
(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明
理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax 2+bx+c上的
动点,当△PDO的周长最小时,求四边形CODP的面积. 中考数学试题
备考第14或25题各年份数学试题
第17题 五种基本作图:
1、作一条线段等于已知线段;
2、作一个角等于已知角;
3、作已知线段的垂直平分线;
4、作已知角的角平分线;
5、过一点作已知直线的垂线; 课标要求的尺规作图:
1、过已知直线外一点作已知直线的平行线;
2、会利用基本作图作三角形:(SSS、SAS、ASA、HL、底边及底边上的高作等腰三角形);
3、会利用基本作图完成:作三角形的外接圆、内切圆;作圆的内接正方形和正六边形.中考数学试题
第17题考法和备考 三数、三差:
1、刻画数据整体水平;
2、刻画数据均衡水平、稳定程度;
三种统计图:
1、扇形
2、折线
3、条形(新增:频数分布直方图)通过统计表和统计图分析,做出判断与决策题;
(平均数、中位数、众数的考查在此体现)预估2017数学试题
第18题考法和备考18题——统计:主要考查学生的数据分析观念18题——统计:主要考查学生的数据分析观念 (2016年)某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.
请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是 ;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
18题——统计:主要考查学生的数据分析观念 (2017年)某养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A、B、C、D四组,如下表所示,同时,将调查结果绘制成下面两幅不完整的统计图.
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布直方图和扇形统计图;
(2)所抽取的七年级学生早锻炼时间的中位数落在 区间内;
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼) 数据的收集、整理与描述
数据的分析
1、理清楚统计的过程:收集数据、整理
数据、分析数据
各年份数学试题
及成因第19题
各年份数学试题
及成因第19题
各年份数学试题
及成因第19题全等三角形3、三角形中线、角分线为背景的全等2、等腰三角形、等边三角形、正方形
为载体的全等1、全等变换下的全等模型考查内容:主要考查全等三角形的证明及利
用全等 后的性质进行证明或简
单计算等关注:以四边形为载体的三角形全等类问题
相关联三角形的全等类问题中考数学试题
第19题考法和备考 20.①(2012陕西20)如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东 45°方向(点A、B、C在同一水平面上).
请你利用小明测得的相关数据,求
湖心岛上的迎宾槐C处与湖岸
上的凉亭A处之间的距离.各年份数学试题
及成因第20题 20.①(2012陕西20)如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东 45°方向(点A、B、C在同一水平面上).
请你利用小明测得的相关数据,求
湖心岛上的迎宾槐C处与湖岸
上的凉亭A处之间的距离.各年份数学试题
及成因第20题20.②(2014陕西20)某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,……
①小明在B点使视线通过帽檐正好落在树的底部点D处,这时小亮测得小明眼睛距地面的距离AB=1.7米;②小明站在原地转动180°后蹲下,这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,求出河宽BD是多少米?
各年份数学试题
及成因第20题
各年份数学试题
及成因第20题 锐角三角函数
投影与视图
2、双直角三角形模型或两对双直角模型1、公式的变形
中考数学试题第20题
备考1、以测量为载体:考察求线段长度
2、知识载体
3、数学本质:方程思想①(2013陕西21)“五一节”期间,申老师一家自架游去了离家170千米的某地.下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求他们出发半小时时,离家多少千米?
(2)求出AB段图象的函数表达式;
(3)他们出发2小时时,
离目的地还有多少千米?各年份数学试题
及成因第21题②(2014陕西21)小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1kg收费22元,超过1kg,则超出部分按每千克10元加收费用.设该公司从西安到南昌快寄樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5kg樱桃,请你求出这次快寄的费用是多少元?
各年份数学试题
及成因第21题
各年份数学试题
及成因第21题
各年份数学试题
及成因第21题
各年份数学试题
及成因第21题考查内容:利用一次函数模型解决问题的能
力(关系式是桥梁)关注:现实背景分段函数类问题
一次函数与不等式的结合
中考数学试题
第21题考法和备考
解答题 第22题:
考点:摸球事件、转盘游戏、纸牌游戏
考法:不超过6、放回、不放回
中考数学试题
第22题考法和备考字母符合、图形语言、表格、文字语言的结合使用孩子的认真,
让人心疼!平均分5.5 满分率59%
2017数学试题
备考内容第25题25题等分—公平问题1、中心对称图形等分面积2、非中心对称类图形等分面积25题等分—公平问题直线过定点等分面积类问题EFD直线过定点等分面积类问题EEMEFM25题—公平问题25题等分—公平问题(6,0)(2,0)(6,4)(2,4)(4,2)25题等分—公平问题 QEGQF25题等分—面积最值类问题分析:面积均为两个因数积的模式思路一:固定一个因数,另外一个因数的大小决定积的 大小思路二:两个因数均为变量,考虑利用完全平方差公式25题等分—面积最值类问题思路三:两个因数用同一个字母表示,出现该字母的二次模式,
利用二次函数求最值25题—面积最值问题ABCDGFHOECCABAEFNPDENMFPHB(2012陕西25)如图,正三角形ABC的边长为 .
(1)如图①,正方形EFPN的顶点E、F在边AB上,顶点N在边AC上.在正三角形及其内部,以A为位似中心,作正方形EFPN的位似正方形 ,且使正方形 的面积最大(不要求写作法)(2)求(1)中作出的正方形 的边长;
(3)如图②,在正三角形ABC中放入正方形DEMN和正方形EFPM,使得DE、EF在边AB上,点P、N分别在边AC、BC上,求这两个正方形面积和的最大值及最小值,并说明理由. 25题——面积最值问题ABAEFNPDENMFPHBCC设正方形E′F′P′N′的边长为a设两个正方形的面积分别为a和b∴两正方形的面积和为S=a2+b2思路一:两个变量用一个去表示,构造二次函数思路二:两个变量的模式,利用完全平方差公式思路三:利用“三兄弟”关系25题——面积最值问题25题——面积最值问题P25题——面积最值问题
中考数学试题
每题考点及成因第25题解答题 第25题:
考点:以几何图形作为载体,考察抽象、推理、
建模,以三角形、四边形、圆为基本图形
考法:充分应用几何演绎推理、代数演绎推理、
解析演绎,数学建模等
备考:最值问题(距离、周长、面积)、
等分问题
- - - 心中有
全卷 时间
安排 背景
可寻 题图
精准 选择有
规则 应试策略四、应试 你准备好了吗?QQ:450889287Thank you!Your site here欢迎批评指正谢谢!应试—2012选择题答案应试—2013选择题答案应试—2014选择题答案应试—2015选择题答案祝各位老师:
心想事成、工作顺利、身体健康
2017年10月最后让我们怀揣着一种爱走近学生,去关心、了解学生,并不遗余力地尊重他们,懂得维护他们的自尊!
同课章节目录
