1.1 锐角三角函数(1)一课一测
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
1.1锐角三角函数
第一课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2016秋 贵池区期末)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )21cnjy.com
A.2 ( http: / / www.21cnjy.com ) B.3 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.(2017春 道里区校级月考)在Rt△ABC中,∠C=90°,BC=1,AB=2,则tanA等于( )www.21-cn-jy.com
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
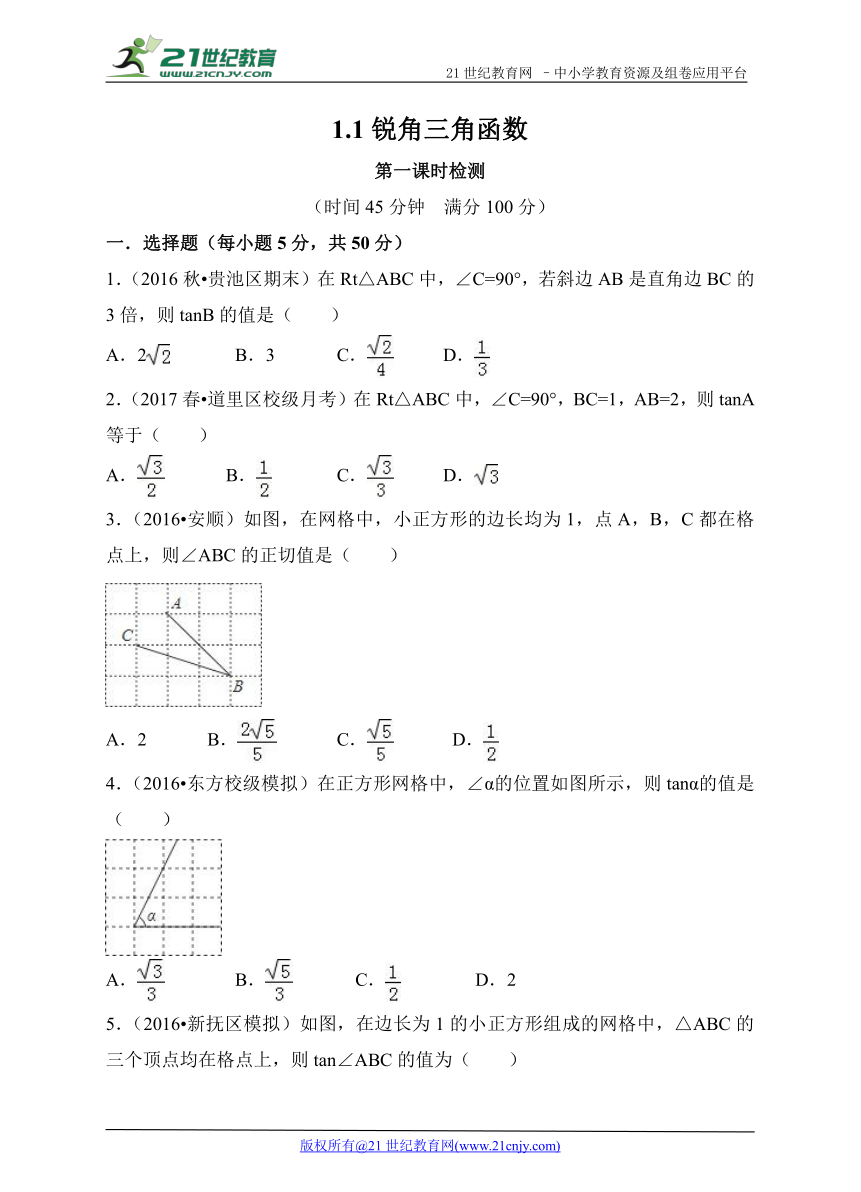
3.(2016 安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.2 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4.(2016 东方校级模拟)在正方形网格中,∠α的位置如图所示,则tanα的值是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.2
5.(2016 新抚区模拟)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
6.(2015秋 东昌府区期末)在Rt△ABC中,∠C=90°,AB=10,tanA= ( http: / / www.21cnjy.com ),则AC的长是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.3 B.4 C.6 D.8
7.(2014秋 福田区期末)比较tan20°,tan50°,tan70°的大小,下列不等式正确的是( )【出处:21教育名师】
A.tan70°<tan50°<tan20° B.tan50°<tan20°<tan70°
C.tan20°<tan50°<tan70° D.tan20°<tan70°<tan50°
8.(2015秋 亭湖区校级期末)在Rt△ABC中,∠C=90°,如果把Rt△ABC的各边的长都缩小为原来的 ( http: / / www.21cnjy.com ),则∠A的正切值( )21教育名师原创作品
A.缩小为原来的 ( http: / / www.21cnjy.com ) B.扩大为原来的4倍
C.缩小为原来的 ( http: / / www.21cnjy.com ) D.没有变化
9.(2015 大庆模拟)如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD= ( http: / / www.21cnjy.com ),则tanA=( )21*cnjy*com
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.1 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
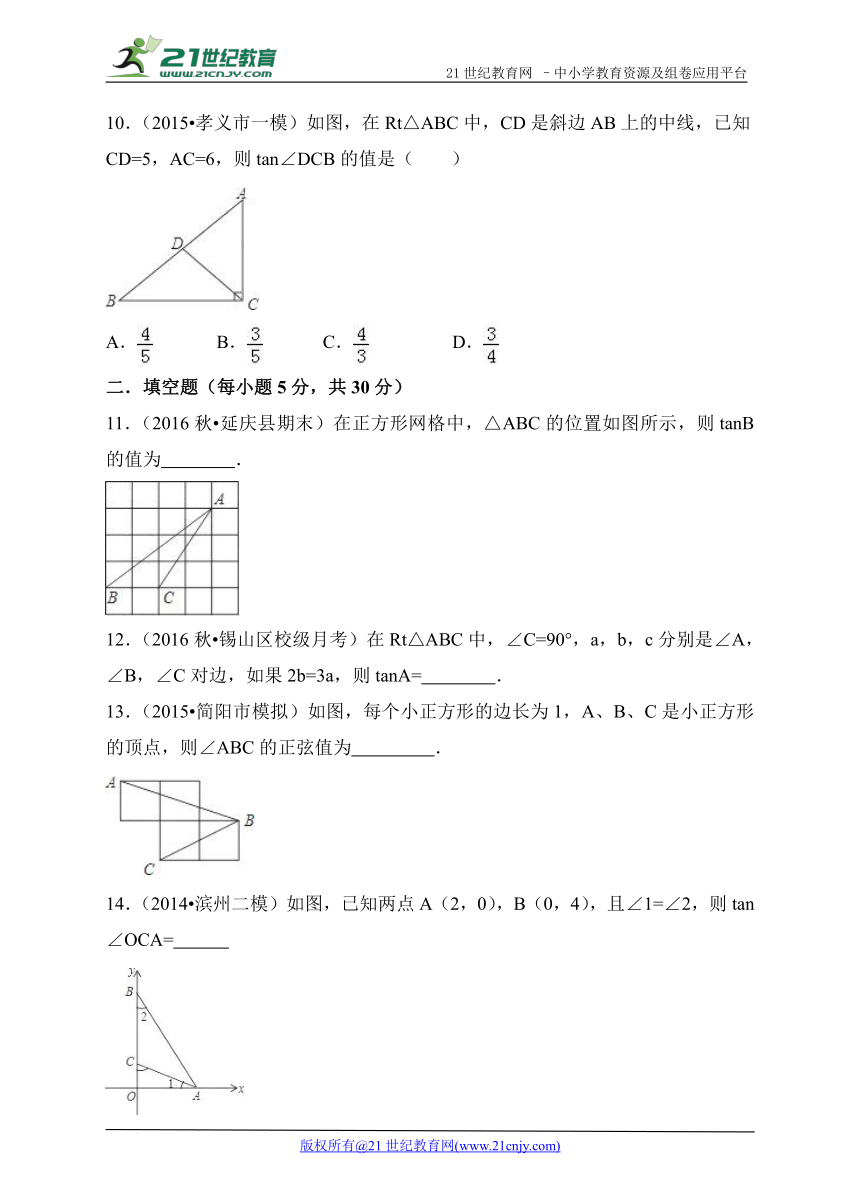
10.(2015 孝义市一模)如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan∠DCB的值是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2016秋 延庆县期末)在正方形网格中,△ABC的位置如图所示,则tanB的值为 .
( http: / / www.21cnjy.com )
12.(2016秋 锡山区校级月考)在R ( http: / / www.21cnjy.com )t△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,如果2b=3a,则tanA= .21·cn·jy·com
13.(2015 简阳市模拟)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 .
( http: / / www.21cnjy.com )
14.(2014 滨州二模)如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA=
( http: / / www.21cnjy.com )
15.(2014 虹口区一模)在Rt△ABC中,∠C=90°,若AC=5,tanA=2,则BC= .
16.(2014 徐汇区一模)如图,已知梯 ( http: / / www.21cnjy.com )形ABCD中,AB∥CD,AB⊥BC,且AD⊥BD,若CD=1,BC=3,那么∠A的正切值为
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2013 温州模拟)如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标.
( http: / / www.21cnjy.com )
18.(10分)(2010秋 杨浦区期中)如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.
( http: / / www.21cnjy.com )
1.1锐角三角函数
第一课时检测
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2016秋 贵池区期末)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )21教育网
A.2 ( http: / / www.21cnjy.com ) B.3 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据勾股定理求出AC,根据正切的概念计算即可.
【解答】解:设BC=x,则AB=3x,
由勾股定理得,AC= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com )x,
则tanB= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
故选:A.
2.(2017春 道里区校级月考)在Rt△ABC中,∠C=90°,BC=1,AB=2,则tanA等于( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据勾股定理求出AC,根据正切的定义计算即可.
【解答】解:∵∠C=90°,BC=1,AB=2,
∴AC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴tanA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故选:C.
3.(2016 安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
( http: / / www.21cnjy.com )
A.2 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据勾股定理,可得AC、AB的长,根据正切函数的定义,可得答案.
【解答】解:如图: ( http: / / www.21cnjy.com ),
由勾股定理,得
AC= ( http: / / www.21cnjy.com ),AB=2 ( http: / / www.21cnjy.com ),BC= ( http: / / www.21cnjy.com ),
∴△ABC为直角三角形,
∴tan∠B= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故选:D.
4.(2016 东方校级模拟)在正方形网格中,∠α的位置如图所示,则tanα的值是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.2
【分析】此题可以根据“角的正切值=对边÷邻边”求解即可.
【解答】解:由图可得,tanα=2÷1=2.
故选D.
( http: / / www.21cnjy.com )
5.(2016 新抚区模拟)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
【分析】先在图中找出∠ABC所在的直角三角形,再根据三角函数的定义即可求出tan∠ABC的值.
【解答】解:如图,在直角△ABD中,AD=3,BD=4,
则tan∠ABC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选B.
( http: / / www.21cnjy.com )
6.(2015秋 东昌府区期末)在Rt△ABC中,∠C=90°,AB=10,tanA= ( http: / / www.21cnjy.com ),则AC的长是( )
( http: / / www.21cnjy.com )
A.3 B.4 C.6 D.8
【分析】根据锐角三角函数正切等于对边比邻边,可得BC与AC的关系,根据勾股定理,可得AC的长.
【解答】解:由tanA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),得
BC=3x,CA=4x,
由勾股定理,得
BC2+AC2=AB2,即(3x)2+(4x)2=100,
解得x=2,
AC=4x=4×2=8.
故选:D.
7.(2014秋 福田区期末)比较tan20°,tan50°,tan70°的大小,下列不等式正确的是( )
A.tan70°<tan50°<tan20° B.tan50°<tan20°<tan70°
C.tan20°<tan50°<tan70° D.tan20°<tan70°<tan50°
【分析】根据正切函数随锐角的增大而增大,可得答案.
【解答】解:由正切函数随角增大而增大,得
tan20°<tan50°<tan70°,故C符合题意,
故选:C.
8.(2015秋 亭湖区校级期末)在Rt△ABC中,∠C=90°,如果把Rt△ABC的各边的长都缩小为原来的 ( http: / / www.21cnjy.com ),则∠A的正切值( )
A.缩小为原来的 ( http: / / www.21cnjy.com ) B.扩大为原来的4倍
C.缩小为原来的 ( http: / / www.21cnjy.com ) D.没有变化
【分析】根据题意得到锐角A的对边与邻边的比值不变,然后根据正切的定义可判断锐角A的正切值不变.
【解答】解:∵在Rt△ABC中,如果每个边都缩小为原来的 ( http: / / www.21cnjy.com ),
∴锐角A的对边与邻边的比值不变,
∴锐角A的正切值不变.
故选D.
9.(2015 大庆模拟)如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD= ( http: / / www.21cnjy.com ),则tanA=( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.1 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】若想利用tan∠BCD的值,应把∠ ( http: / / www.21cnjy.com )BCD放在直角三角形中,也就得到了Rt△ACD的中位线,可分别得到所求的角的正切值相关的线段的比.
【解答】解:过B作BE∥AC交CD于E.
∵AC⊥BC,
∴BE⊥BC,∠CBE=90°.
∴BE∥AC.
∵AB=BD,
∴AC=2BE.
又∵tan∠BCD= ( http: / / www.21cnjy.com ),设BE=x,则AC=2x,
∴tanA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故选A.
( http: / / www.21cnjy.com )
10.(2015 孝义市一模)如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan∠DCB的值是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据直角三角形的性 ( http: / / www.21cnjy.com )质,可得AB的长,根据勾股定理,可得BC的长,根据等腰三角形的性质,可得CE的长,根据锐角三角函数的定义,可得答案.
【解答】解:作DE⊥BC于E,
( http: / / www.21cnjy.com )
由直角三角形的性质,得
AB=2CD=2BD=10.
由勾股定理,得
BC=8,
由等腰三角形的性质,得
CE= ( http: / / www.21cnjy.com )BC=4,
由勾股定理,得
DE= ( http: / / www.21cnjy.com )=3,
tan∠DCB= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选:D.
二.填空题(每小题5分,共30分)
11.(2016秋 延庆县期末)在正方形网格中,△ABC的位置如图所示,则tanB的值为 ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】利用锐角三角函数关系直接得出答案.
【解答】解:如图所示:tanB= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故答案为: ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
12.(2016秋 锡山区校级月考)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,如果2b=3a,则tanA= ( http: / / www.21cnjy.com ) .21·世纪*教育网
【分析】根据锐角三角函数的定义可得tanA= ( http: / / www.21cnjy.com ),然后根据题目所给2b=3a可求解.
【解答】解:∵∠C=90°,a,b,c分别是∠A,∠B,∠C对边,
∴tanA= ( http: / / www.21cnjy.com ),
∵2b=3a,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴tanA= ( http: / / www.21cnjy.com ).
故答案为: ( http: / / www.21cnjy.com ).
13.(2015 简阳市模拟)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 ( http: / / www.21cnjy.com ) .2-1-c-n-j-y
( http: / / www.21cnjy.com )
【分析】首先利用勾股定理计算出AB2, ( http: / / www.21cnjy.com )BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
【解答】解:AB2=32+12=10,BC2=22+12=5,AC2=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=45°,
∴∠ABC的正弦值为 ( http: / / www.21cnjy.com ).
故答案为: ( http: / / www.21cnjy.com ).
14.(2014 滨州二模)如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA= 2 .
( http: / / www.21cnjy.com )
【分析】首先根据三角形内角和可得∠BAO=∠ACO,再根据正切定义计算出tan∠OCA.
【解答】解:∵∠1=∠2,
∴∠BAO=∠ACO,
∵A(2,0),B(0,4),
∴tan∠OCA=tan∠BAO= ( http: / / www.21cnjy.com )=2.
故答案为:2.
15.(2014 虹口区一模)在Rt△ABC中,∠C=90°,若AC=5,tanA=2,则BC= 10 .【版权所有:21教育】
【分析】根据正切函数的定义即可求解.
【解答】解:∵tanA= ( http: / / www.21cnjy.com ),
∴BC=AC tanA=5×2=10.
故答案是:10.
16.(2014 徐汇区一模)如图,已知梯形ABCD中,AB∥CD,AB⊥BC,且AD⊥BD,若CD=1,BC=3,那么∠A的正切值为 ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】求出∠ABC=∠ADB=90°,根据三角形内角和定理求出∠A=∠DBC,解直角三角形求出即可.
【解答】解:∵AB∥CD,AB⊥BC,
∴DC⊥BC,∠ABC=90°,
∴∠C=90°,
∵AD⊥BD,
∴∠ADB=90°,
∴∠DBC+∠ABD=∠A+∠ABD=90°,
∴∠A=∠DBC,
∵CD=1,BC=3,
∴∠A的正切值为tanA=tan∠DBC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com ).
三.解答题(共20分)
17.(2013 温州模拟)如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标.
( http: / / www.21cnjy.com )
【分析】(1)根据正切的定义,对边与相邻的斜边的比,即可求解;
(2)根据图形,确定旋转以后的位置,可以直接写出坐标.
【解答】解:(1)tan∠BOA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com );
(2)点C的坐标是(﹣2,4).
18.(2010秋 杨浦区期中)如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.21世纪教育网版权所有
( http: / / www.21cnjy.com )
【分析】根据题意画出图形,由三角形的面积公式求出AH的长,再由勾股定理求出BH的长,最后由锐角三角函数的定义即可解答.21*cnjy*com
【解答】解:过点A作AH⊥BC于H,
∵S△ABC=27,
∴ ( http: / / www.21cnjy.com ),
∴AH=6,
∵AB=10,
∴BH= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=8,
∴tanB= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
1.1锐角三角函数
第一课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2016秋 贵池区期末)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )21cnjy.com
A.2 ( http: / / www.21cnjy.com ) B.3 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.(2017春 道里区校级月考)在Rt△ABC中,∠C=90°,BC=1,AB=2,则tanA等于( )www.21-cn-jy.com
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
3.(2016 安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.2 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4.(2016 东方校级模拟)在正方形网格中,∠α的位置如图所示,则tanα的值是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.2
5.(2016 新抚区模拟)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
6.(2015秋 东昌府区期末)在Rt△ABC中,∠C=90°,AB=10,tanA= ( http: / / www.21cnjy.com ),则AC的长是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.3 B.4 C.6 D.8
7.(2014秋 福田区期末)比较tan20°,tan50°,tan70°的大小,下列不等式正确的是( )【出处:21教育名师】
A.tan70°<tan50°<tan20° B.tan50°<tan20°<tan70°
C.tan20°<tan50°<tan70° D.tan20°<tan70°<tan50°
8.(2015秋 亭湖区校级期末)在Rt△ABC中,∠C=90°,如果把Rt△ABC的各边的长都缩小为原来的 ( http: / / www.21cnjy.com ),则∠A的正切值( )21教育名师原创作品
A.缩小为原来的 ( http: / / www.21cnjy.com ) B.扩大为原来的4倍
C.缩小为原来的 ( http: / / www.21cnjy.com ) D.没有变化
9.(2015 大庆模拟)如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD= ( http: / / www.21cnjy.com ),则tanA=( )21*cnjy*com
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.1 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
10.(2015 孝义市一模)如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan∠DCB的值是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(每小题5分,共30分)
11.(2016秋 延庆县期末)在正方形网格中,△ABC的位置如图所示,则tanB的值为 .
( http: / / www.21cnjy.com )
12.(2016秋 锡山区校级月考)在R ( http: / / www.21cnjy.com )t△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,如果2b=3a,则tanA= .21·cn·jy·com
13.(2015 简阳市模拟)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 .
( http: / / www.21cnjy.com )
14.(2014 滨州二模)如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA=
( http: / / www.21cnjy.com )
15.(2014 虹口区一模)在Rt△ABC中,∠C=90°,若AC=5,tanA=2,则BC= .
16.(2014 徐汇区一模)如图,已知梯 ( http: / / www.21cnjy.com )形ABCD中,AB∥CD,AB⊥BC,且AD⊥BD,若CD=1,BC=3,那么∠A的正切值为
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2013 温州模拟)如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标.
( http: / / www.21cnjy.com )
18.(10分)(2010秋 杨浦区期中)如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.
( http: / / www.21cnjy.com )
1.1锐角三角函数
第一课时检测
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2016秋 贵池区期末)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )21教育网
A.2 ( http: / / www.21cnjy.com ) B.3 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据勾股定理求出AC,根据正切的概念计算即可.
【解答】解:设BC=x,则AB=3x,
由勾股定理得,AC= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com )x,
则tanB= ( http: / / www.21cnjy.com )=2 ( http: / / www.21cnjy.com ),
故选:A.
2.(2017春 道里区校级月考)在Rt△ABC中,∠C=90°,BC=1,AB=2,则tanA等于( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据勾股定理求出AC,根据正切的定义计算即可.
【解答】解:∵∠C=90°,BC=1,AB=2,
∴AC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴tanA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故选:C.
3.(2016 安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
( http: / / www.21cnjy.com )
A.2 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据勾股定理,可得AC、AB的长,根据正切函数的定义,可得答案.
【解答】解:如图: ( http: / / www.21cnjy.com ),
由勾股定理,得
AC= ( http: / / www.21cnjy.com ),AB=2 ( http: / / www.21cnjy.com ),BC= ( http: / / www.21cnjy.com ),
∴△ABC为直角三角形,
∴tan∠B= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故选:D.
4.(2016 东方校级模拟)在正方形网格中,∠α的位置如图所示,则tanα的值是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.2
【分析】此题可以根据“角的正切值=对边÷邻边”求解即可.
【解答】解:由图可得,tanα=2÷1=2.
故选D.
( http: / / www.21cnjy.com )
5.(2016 新抚区模拟)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D.1
【分析】先在图中找出∠ABC所在的直角三角形,再根据三角函数的定义即可求出tan∠ABC的值.
【解答】解:如图,在直角△ABD中,AD=3,BD=4,
则tan∠ABC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选B.
( http: / / www.21cnjy.com )
6.(2015秋 东昌府区期末)在Rt△ABC中,∠C=90°,AB=10,tanA= ( http: / / www.21cnjy.com ),则AC的长是( )
( http: / / www.21cnjy.com )
A.3 B.4 C.6 D.8
【分析】根据锐角三角函数正切等于对边比邻边,可得BC与AC的关系,根据勾股定理,可得AC的长.
【解答】解:由tanA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),得
BC=3x,CA=4x,
由勾股定理,得
BC2+AC2=AB2,即(3x)2+(4x)2=100,
解得x=2,
AC=4x=4×2=8.
故选:D.
7.(2014秋 福田区期末)比较tan20°,tan50°,tan70°的大小,下列不等式正确的是( )
A.tan70°<tan50°<tan20° B.tan50°<tan20°<tan70°
C.tan20°<tan50°<tan70° D.tan20°<tan70°<tan50°
【分析】根据正切函数随锐角的增大而增大,可得答案.
【解答】解:由正切函数随角增大而增大,得
tan20°<tan50°<tan70°,故C符合题意,
故选:C.
8.(2015秋 亭湖区校级期末)在Rt△ABC中,∠C=90°,如果把Rt△ABC的各边的长都缩小为原来的 ( http: / / www.21cnjy.com ),则∠A的正切值( )
A.缩小为原来的 ( http: / / www.21cnjy.com ) B.扩大为原来的4倍
C.缩小为原来的 ( http: / / www.21cnjy.com ) D.没有变化
【分析】根据题意得到锐角A的对边与邻边的比值不变,然后根据正切的定义可判断锐角A的正切值不变.
【解答】解:∵在Rt△ABC中,如果每个边都缩小为原来的 ( http: / / www.21cnjy.com ),
∴锐角A的对边与邻边的比值不变,
∴锐角A的正切值不变.
故选D.
9.(2015 大庆模拟)如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD= ( http: / / www.21cnjy.com ),则tanA=( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B.1 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】若想利用tan∠BCD的值,应把∠ ( http: / / www.21cnjy.com )BCD放在直角三角形中,也就得到了Rt△ACD的中位线,可分别得到所求的角的正切值相关的线段的比.
【解答】解:过B作BE∥AC交CD于E.
∵AC⊥BC,
∴BE⊥BC,∠CBE=90°.
∴BE∥AC.
∵AB=BD,
∴AC=2BE.
又∵tan∠BCD= ( http: / / www.21cnjy.com ),设BE=x,则AC=2x,
∴tanA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故选A.
( http: / / www.21cnjy.com )
10.(2015 孝义市一模)如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan∠DCB的值是( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据直角三角形的性 ( http: / / www.21cnjy.com )质,可得AB的长,根据勾股定理,可得BC的长,根据等腰三角形的性质,可得CE的长,根据锐角三角函数的定义,可得答案.
【解答】解:作DE⊥BC于E,
( http: / / www.21cnjy.com )
由直角三角形的性质,得
AB=2CD=2BD=10.
由勾股定理,得
BC=8,
由等腰三角形的性质,得
CE= ( http: / / www.21cnjy.com )BC=4,
由勾股定理,得
DE= ( http: / / www.21cnjy.com )=3,
tan∠DCB= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故选:D.
二.填空题(每小题5分,共30分)
11.(2016秋 延庆县期末)在正方形网格中,△ABC的位置如图所示,则tanB的值为 ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】利用锐角三角函数关系直接得出答案.
【解答】解:如图所示:tanB= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故答案为: ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
12.(2016秋 锡山区校级月考)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C对边,如果2b=3a,则tanA= ( http: / / www.21cnjy.com ) .21·世纪*教育网
【分析】根据锐角三角函数的定义可得tanA= ( http: / / www.21cnjy.com ),然后根据题目所给2b=3a可求解.
【解答】解:∵∠C=90°,a,b,c分别是∠A,∠B,∠C对边,
∴tanA= ( http: / / www.21cnjy.com ),
∵2b=3a,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴tanA= ( http: / / www.21cnjy.com ).
故答案为: ( http: / / www.21cnjy.com ).
13.(2015 简阳市模拟)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 ( http: / / www.21cnjy.com ) .2-1-c-n-j-y
( http: / / www.21cnjy.com )
【分析】首先利用勾股定理计算出AB2, ( http: / / www.21cnjy.com )BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
【解答】解:AB2=32+12=10,BC2=22+12=5,AC2=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=45°,
∴∠ABC的正弦值为 ( http: / / www.21cnjy.com ).
故答案为: ( http: / / www.21cnjy.com ).
14.(2014 滨州二模)如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA= 2 .
( http: / / www.21cnjy.com )
【分析】首先根据三角形内角和可得∠BAO=∠ACO,再根据正切定义计算出tan∠OCA.
【解答】解:∵∠1=∠2,
∴∠BAO=∠ACO,
∵A(2,0),B(0,4),
∴tan∠OCA=tan∠BAO= ( http: / / www.21cnjy.com )=2.
故答案为:2.
15.(2014 虹口区一模)在Rt△ABC中,∠C=90°,若AC=5,tanA=2,则BC= 10 .【版权所有:21教育】
【分析】根据正切函数的定义即可求解.
【解答】解:∵tanA= ( http: / / www.21cnjy.com ),
∴BC=AC tanA=5×2=10.
故答案是:10.
16.(2014 徐汇区一模)如图,已知梯形ABCD中,AB∥CD,AB⊥BC,且AD⊥BD,若CD=1,BC=3,那么∠A的正切值为 ( http: / / www.21cnjy.com ) .
( http: / / www.21cnjy.com )
【分析】求出∠ABC=∠ADB=90°,根据三角形内角和定理求出∠A=∠DBC,解直角三角形求出即可.
【解答】解:∵AB∥CD,AB⊥BC,
∴DC⊥BC,∠ABC=90°,
∴∠C=90°,
∵AD⊥BD,
∴∠ADB=90°,
∴∠DBC+∠ABD=∠A+∠ABD=90°,
∴∠A=∠DBC,
∵CD=1,BC=3,
∴∠A的正切值为tanA=tan∠DBC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com ).
三.解答题(共20分)
17.(2013 温州模拟)如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标.
( http: / / www.21cnjy.com )
【分析】(1)根据正切的定义,对边与相邻的斜边的比,即可求解;
(2)根据图形,确定旋转以后的位置,可以直接写出坐标.
【解答】解:(1)tan∠BOA= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com );
(2)点C的坐标是(﹣2,4).
18.(2010秋 杨浦区期中)如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.21世纪教育网版权所有
( http: / / www.21cnjy.com )
【分析】根据题意画出图形,由三角形的面积公式求出AH的长,再由勾股定理求出BH的长,最后由锐角三角函数的定义即可解答.21*cnjy*com
【解答】解:过点A作AH⊥BC于H,
∵S△ABC=27,
∴ ( http: / / www.21cnjy.com ),
∴AH=6,
∵AB=10,
∴BH= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=8,
∴tanB= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
