25.1.2 概率 课件
图片预览











文档简介
课件32张PPT。概 率 1.在具体情境中了解概率的意义.
2.会求简单问题中某一事件的概率. 在第二次世界大战中,美国曾经宣布:一名优秀数学家的作用超过10个师的兵力.这句话有一个非同寻常的来历.
1943年以前,在大西洋上英美运输船队常常受到德国潜艇的袭击,当时,英美两国限于实力,无力增派更多的护航舰.一时间,德军的“潜艇战”搞得盟军焦头烂额.1名数学家=10个师为此,有位美国海军将领专门去请教了一位数学家,数学家们运用概率论分析后认为:舰队与敌潜艇相遇是一个随机事件,从数学角度来看这一问题,它具有一定的规律性.一定数量的船(为100艘)编队规模越小,编次就越多(为每次20艘,就要有5个编次).编次越多,与敌人相遇的概率就越大.
美国海军接受了数学家的建议,命令舰队在指定海域集合,再集体通过危险海域,然后各自驶向预定港口.结果奇迹出现了:盟军舰队遭袭被击沉的概率由原来的25%降为1%,大大减少了损失,保证了物资的及时供应.【思考】分析这些事件发生与否,各有什么特点?
(1)“地球不停地转动”
(2)“木柴燃烧,产生能量”
(3)“在常温下,石头一天被风化”
(4)“某人射击一次,击中十环”
(5)“掷一枚硬币,出现正面”
(6)“在标准大气压下且温度低于 0℃时,雪融化”(1)“地球不停地运动”是必然事件.
(2)“木柴燃烧,产生热量”是必然事件.
(3)“在常温下,石头一天被风化”是不可能事件.
(4)“某人射击一次,击中十环”是可能发生也可能不发生事件,事先无法知道.
(5)“掷一枚硬币,出现正面”是可能发生也可能不发生事件,事先无法知道.
(6)“在标准大气压下且温度低于0℃时,雪融化”是不可能事件. 2010年10月17日 晴
早上,我迟到了.于是就急忙去学校上学,可是在楼梯上遇到了班主任,她批评了我一顿.我想我真不走运,她经常在办公室的啊,今天我真倒霉.我明天不能再迟到了,不然明天早上我将在楼梯上遇到班主任.
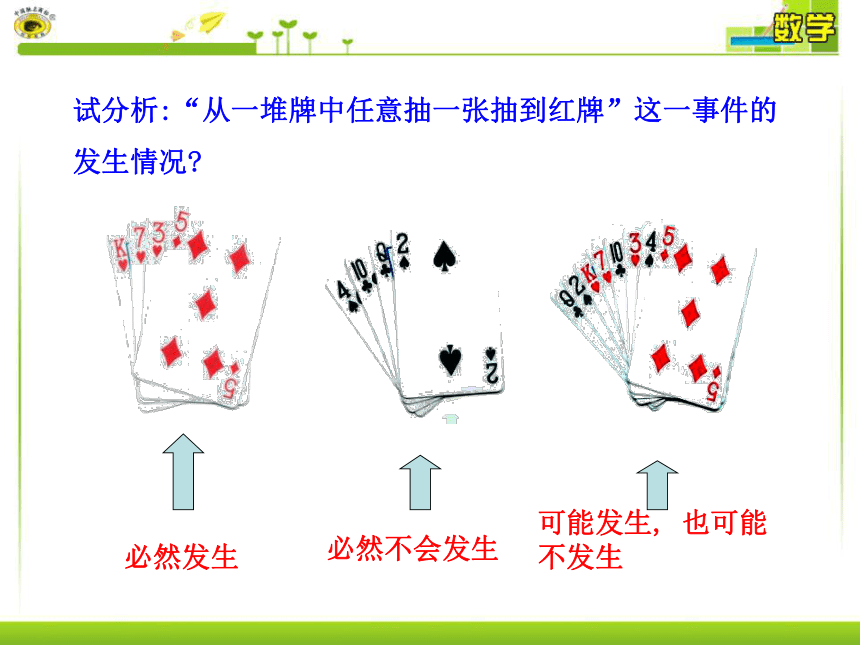
中午放学回家,我看了一场篮球赛,我想长大后我会比姚明还高,我将长到100米高.看完比赛后,我又回到学校上学. 下午放学后,我开始写作业.今天作业太多了,我不停的写啊,一直写到太阳从西边落下.小明从盒中任意摸出一球,一定能摸到红球吗?小麦从盒中摸出的球一定是白球吗?小米从盒中摸出的球一定是红球吗?三人每次都能摸到红球吗? 同学们听过“天有不测风云”这句话吧!它的原意是指刮风、下雨、阴天、晴天这些天气状况很难预料,后来它被引申为:世界上很多事情具有偶然性,人们不能事先判定这些事情是否会发生.试分析:“从一堆牌中任意抽一张抽到红牌”这一事件的发生情况?可能发生, 也可能不发生必然发生必然不会发生 5名同学参加演讲比赛,以抽签方式决定每个人的出场顺序.签筒中有5根形状大小相同的纸签,上面分别标有出场的序号1,2,3,4,5.小军首先抽签,他在看不到的纸签上的数字的情况从签筒中随机(任意)地取一根纸签.请考虑以下问题: (1)抽到的序号有几种可能的结果? (2)抽到的序号会是0吗? (3)抽到的序号小于6吗? (4)抽到的序号会是1吗? (5)你能列举与事件(3)相似的事件吗? 小伟掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有1至6的点数.请考虑以下问题,掷一次骰子,观察骰子向上的一面: (1)可能出现哪些点数? (2)出现的点数会是7吗? (3)出现的点数大于0吗? (4)出现的点数会是4吗? (5)你能列举与事件(3)相似的事件吗? 摸球试验:袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球. (1)这个球是白球还是黑球?(2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗?归纳:一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同.思考:能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?(1)一个袋子里装有20个形状、质地、大小一样的球,其中4个白球,2个红球,3个黑球,其它都是黄球,从中任摸一个,摸中哪种球的可能性最大?
(2)一个人随意翻书三次,三次都翻到了偶数页,我们能否说翻到偶数页的可能性就大?(3)袋子里装有红、白两种颜色的小球,质地、大小、形状一样,小明从中随机摸出一个球,然后放回,如果小明5次摸到红球,能否断定袋子里红球的数量比白球多?怎样做才能判断哪种颜色的球数量较多?
(4)已知地球表面陆地面积与海洋面积的比均为3:7.如果宇宙中飞来一块陨石落在地球上,“落在海洋里”与“落在陆地上”哪个可能性更大? 全班分成八组,每组同学掷一枚硬币30次,
记录好“正面向上”的次数,
计算出“正面向上”的频率.抛掷次数n“正面向上”的频数m“正面向上”的频率m/n投掷次数正面向上的频率m/n0501001502002503000.51根据实验所得的数据想一想:
“正面向上” 的频率有什么规律?随着抛掷次数的增加,“正面向上”的频率的变化趋势有何规律? 一般地,在大量重复试验中,如果事件A发生的频率m/n稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记为P(A)=p.
事件一般用大写英文字母A,B,C,D...表示 因为在n次试验中,事件A发生的频数m满足
0≤m≤n ,所以0≤m/n≤1 ,进而可知频率m/n所稳定到的常数p满足0≤m/n≤1,因此0≤P(A)≤1.小组议一议:p的取值范围1、当A是必然发生的事件时,P(A)是多少2、当A是不可能发生的事件时,P(A)是多少 当A是必然发生的事件时,在n次实验中,事件A发生的频数m=n,相应的频率m/n=n/n=1,随着n的增加频率始终稳定地为1,因此P(A)=1.事件发生的可能性越来越大事件发生的可能性越来越小不可能发生必然发生概率的值1.当A是必然发生的事件时,P(A)= ____________.
当B是不可能发生的事件时,P(B)=___________.
当C是随机事件时,P(C)的范围是____________.2.投掷一枚骰子,出现点数不超过4的概率约是______.3.一次抽奖活动中,印发奖券10 000张,其中一等奖
一名奖金5000元,那么第一位抽奖者,(仅买一张)
中奖概率为____________.100≤P(C)≤10.6671/10000从上面可知,概率是通过大量重复试验中频率的稳定性得到的一个0-1的常数,它反映了事件发生的可能性的大小.需要注意,概率是针对大量试验而言的,大量试验反映的规律并非在每次试验中一定存在.1.(盐城·中考)不透明的袋子中装有4个红球、3个黄球和5个蓝球,每个球除颜色不同外其它都相同,从中任意摸出一个球,则摸出 球的可能性最大.【解析】总球数为12个,摸出蓝球的概率为5/12,摸出红球的概率为4/12=1/3,摸出黄球的概率为3/12=1/4.所以摸出蓝球的可能性大.
答案:蓝.2.(苏州·中考)一个不透明的盒子中放着编
号为1到10的10张卡片(编号均为正整数),这些卡片除
了编号以外没有任何其他区别.盒中卡片已经搅匀.
从中随机地抽出1张卡片,则“该卡片上的数字大于
”的概率是 .
【解析】因为卡片上的数字都是正整数,概率大于
即概率大于5.因为大于5和小于5的数字相同,
所以抽到大于 ”的概率是 .
答案: 3.(青岛·中考)一个口袋中装有10个红球和若干个黄
球.在不允许将球倒出来数的前提下,为估计口袋中黄球的
个数,小明采用了如下的方法:每次先从口袋中摸出10个
球,求出其中红球数与10的比值,再把球放回口袋中摇匀.
不断重复上述过程20次,得到红球数与10的比值的平均数为
0.4.根据上述数据,估计口袋中大约有_____个黄球.【解析】由题意可知试验中的摸出红球的频率是0.4,因此可以认为口袋里摸出红球的概率是0.4,则口袋里的球的个数为10÷0.4=25(个),所以口袋里大约有黄球15个.
答案:154.袋子里有1个红球、3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则P(摸到红球)= ; P(摸到白球)= ;P(摸到黄球)= .【解析】按逆时针共有下列六种不同的坐法:ABCD、ABDC、ACBD、ACDB、ADBC、ADCB ,而A与B不相邻的有2种,所以A与B不相邻而坐的概率为5.彩票有100张,分别标有1,2,3,…100的号码,只有摸中的号码是7的倍数的彩券才有奖,小明随机地摸出一张,那么他中奖的概率是多少?
6.一张圆桌旁有4个座位,A先坐在如图所示的位置上,B、C、D随机地坐到其它三个座位上,求A与B不相邻而坐的概率.1.在具体情境中了解概率的意义.
2.会求简单问题中某一事件的概率.通过本课时的学习,需要我们: 数学,科学的女皇;数论,数学的女皇.
—高斯
2.会求简单问题中某一事件的概率. 在第二次世界大战中,美国曾经宣布:一名优秀数学家的作用超过10个师的兵力.这句话有一个非同寻常的来历.
1943年以前,在大西洋上英美运输船队常常受到德国潜艇的袭击,当时,英美两国限于实力,无力增派更多的护航舰.一时间,德军的“潜艇战”搞得盟军焦头烂额.1名数学家=10个师为此,有位美国海军将领专门去请教了一位数学家,数学家们运用概率论分析后认为:舰队与敌潜艇相遇是一个随机事件,从数学角度来看这一问题,它具有一定的规律性.一定数量的船(为100艘)编队规模越小,编次就越多(为每次20艘,就要有5个编次).编次越多,与敌人相遇的概率就越大.
美国海军接受了数学家的建议,命令舰队在指定海域集合,再集体通过危险海域,然后各自驶向预定港口.结果奇迹出现了:盟军舰队遭袭被击沉的概率由原来的25%降为1%,大大减少了损失,保证了物资的及时供应.【思考】分析这些事件发生与否,各有什么特点?
(1)“地球不停地转动”
(2)“木柴燃烧,产生能量”
(3)“在常温下,石头一天被风化”
(4)“某人射击一次,击中十环”
(5)“掷一枚硬币,出现正面”
(6)“在标准大气压下且温度低于 0℃时,雪融化”(1)“地球不停地运动”是必然事件.
(2)“木柴燃烧,产生热量”是必然事件.
(3)“在常温下,石头一天被风化”是不可能事件.
(4)“某人射击一次,击中十环”是可能发生也可能不发生事件,事先无法知道.
(5)“掷一枚硬币,出现正面”是可能发生也可能不发生事件,事先无法知道.
(6)“在标准大气压下且温度低于0℃时,雪融化”是不可能事件. 2010年10月17日 晴
早上,我迟到了.于是就急忙去学校上学,可是在楼梯上遇到了班主任,她批评了我一顿.我想我真不走运,她经常在办公室的啊,今天我真倒霉.我明天不能再迟到了,不然明天早上我将在楼梯上遇到班主任.
中午放学回家,我看了一场篮球赛,我想长大后我会比姚明还高,我将长到100米高.看完比赛后,我又回到学校上学. 下午放学后,我开始写作业.今天作业太多了,我不停的写啊,一直写到太阳从西边落下.小明从盒中任意摸出一球,一定能摸到红球吗?小麦从盒中摸出的球一定是白球吗?小米从盒中摸出的球一定是红球吗?三人每次都能摸到红球吗? 同学们听过“天有不测风云”这句话吧!它的原意是指刮风、下雨、阴天、晴天这些天气状况很难预料,后来它被引申为:世界上很多事情具有偶然性,人们不能事先判定这些事情是否会发生.试分析:“从一堆牌中任意抽一张抽到红牌”这一事件的发生情况?可能发生, 也可能不发生必然发生必然不会发生 5名同学参加演讲比赛,以抽签方式决定每个人的出场顺序.签筒中有5根形状大小相同的纸签,上面分别标有出场的序号1,2,3,4,5.小军首先抽签,他在看不到的纸签上的数字的情况从签筒中随机(任意)地取一根纸签.请考虑以下问题: (1)抽到的序号有几种可能的结果? (2)抽到的序号会是0吗? (3)抽到的序号小于6吗? (4)抽到的序号会是1吗? (5)你能列举与事件(3)相似的事件吗? 小伟掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有1至6的点数.请考虑以下问题,掷一次骰子,观察骰子向上的一面: (1)可能出现哪些点数? (2)出现的点数会是7吗? (3)出现的点数大于0吗? (4)出现的点数会是4吗? (5)你能列举与事件(3)相似的事件吗? 摸球试验:袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球. (1)这个球是白球还是黑球?(2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗?归纳:一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同.思考:能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?(1)一个袋子里装有20个形状、质地、大小一样的球,其中4个白球,2个红球,3个黑球,其它都是黄球,从中任摸一个,摸中哪种球的可能性最大?
(2)一个人随意翻书三次,三次都翻到了偶数页,我们能否说翻到偶数页的可能性就大?(3)袋子里装有红、白两种颜色的小球,质地、大小、形状一样,小明从中随机摸出一个球,然后放回,如果小明5次摸到红球,能否断定袋子里红球的数量比白球多?怎样做才能判断哪种颜色的球数量较多?
(4)已知地球表面陆地面积与海洋面积的比均为3:7.如果宇宙中飞来一块陨石落在地球上,“落在海洋里”与“落在陆地上”哪个可能性更大? 全班分成八组,每组同学掷一枚硬币30次,
记录好“正面向上”的次数,
计算出“正面向上”的频率.抛掷次数n“正面向上”的频数m“正面向上”的频率m/n投掷次数正面向上的频率m/n0501001502002503000.51根据实验所得的数据想一想:
“正面向上” 的频率有什么规律?随着抛掷次数的增加,“正面向上”的频率的变化趋势有何规律? 一般地,在大量重复试验中,如果事件A发生的频率m/n稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记为P(A)=p.
事件一般用大写英文字母A,B,C,D...表示 因为在n次试验中,事件A发生的频数m满足
0≤m≤n ,所以0≤m/n≤1 ,进而可知频率m/n所稳定到的常数p满足0≤m/n≤1,因此0≤P(A)≤1.小组议一议:p的取值范围1、当A是必然发生的事件时,P(A)是多少2、当A是不可能发生的事件时,P(A)是多少 当A是必然发生的事件时,在n次实验中,事件A发生的频数m=n,相应的频率m/n=n/n=1,随着n的增加频率始终稳定地为1,因此P(A)=1.事件发生的可能性越来越大事件发生的可能性越来越小不可能发生必然发生概率的值1.当A是必然发生的事件时,P(A)= ____________.
当B是不可能发生的事件时,P(B)=___________.
当C是随机事件时,P(C)的范围是____________.2.投掷一枚骰子,出现点数不超过4的概率约是______.3.一次抽奖活动中,印发奖券10 000张,其中一等奖
一名奖金5000元,那么第一位抽奖者,(仅买一张)
中奖概率为____________.100≤P(C)≤10.6671/10000从上面可知,概率是通过大量重复试验中频率的稳定性得到的一个0-1的常数,它反映了事件发生的可能性的大小.需要注意,概率是针对大量试验而言的,大量试验反映的规律并非在每次试验中一定存在.1.(盐城·中考)不透明的袋子中装有4个红球、3个黄球和5个蓝球,每个球除颜色不同外其它都相同,从中任意摸出一个球,则摸出 球的可能性最大.【解析】总球数为12个,摸出蓝球的概率为5/12,摸出红球的概率为4/12=1/3,摸出黄球的概率为3/12=1/4.所以摸出蓝球的可能性大.
答案:蓝.2.(苏州·中考)一个不透明的盒子中放着编
号为1到10的10张卡片(编号均为正整数),这些卡片除
了编号以外没有任何其他区别.盒中卡片已经搅匀.
从中随机地抽出1张卡片,则“该卡片上的数字大于
”的概率是 .
【解析】因为卡片上的数字都是正整数,概率大于
即概率大于5.因为大于5和小于5的数字相同,
所以抽到大于 ”的概率是 .
答案: 3.(青岛·中考)一个口袋中装有10个红球和若干个黄
球.在不允许将球倒出来数的前提下,为估计口袋中黄球的
个数,小明采用了如下的方法:每次先从口袋中摸出10个
球,求出其中红球数与10的比值,再把球放回口袋中摇匀.
不断重复上述过程20次,得到红球数与10的比值的平均数为
0.4.根据上述数据,估计口袋中大约有_____个黄球.【解析】由题意可知试验中的摸出红球的频率是0.4,因此可以认为口袋里摸出红球的概率是0.4,则口袋里的球的个数为10÷0.4=25(个),所以口袋里大约有黄球15个.
答案:154.袋子里有1个红球、3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则P(摸到红球)= ; P(摸到白球)= ;P(摸到黄球)= .【解析】按逆时针共有下列六种不同的坐法:ABCD、ABDC、ACBD、ACDB、ADBC、ADCB ,而A与B不相邻的有2种,所以A与B不相邻而坐的概率为5.彩票有100张,分别标有1,2,3,…100的号码,只有摸中的号码是7的倍数的彩券才有奖,小明随机地摸出一张,那么他中奖的概率是多少?
6.一张圆桌旁有4个座位,A先坐在如图所示的位置上,B、C、D随机地坐到其它三个座位上,求A与B不相邻而坐的概率.1.在具体情境中了解概率的意义.
2.会求简单问题中某一事件的概率.通过本课时的学习,需要我们: 数学,科学的女皇;数论,数学的女皇.
—高斯
同课章节目录
