1.6 利用三角函数测高一课一测
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
1.6利用三角函数测高检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
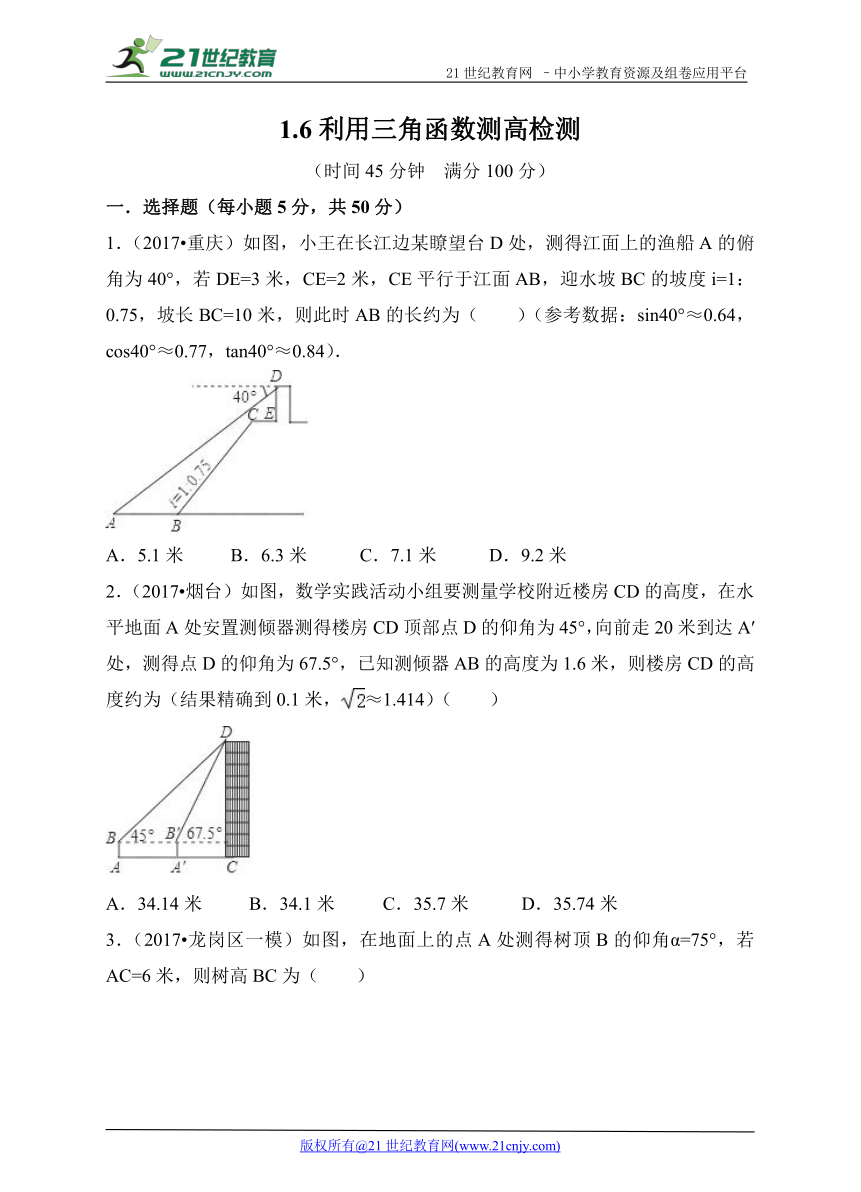
1.(2017 重庆)如图,小王在长江边 ( http: / / www.21cnjy.com )某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).21*cnjy*com
( http: / / www.21cnjy.com )
A.5.1米 B.6.3米 C.7.1米 D.9.2米
2.(2017 烟台)如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ( http: / / www.21cnjy.com )≈1.414)( )
( http: / / www.21cnjy.com )
A.34.14米 B.34.1米 C.35.7米 D.35.74米
3.(2017 龙岗区一模)如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
( http: / / www.21cnjy.com )
A.6sin75°米 B. ( http: / / www.21cnjy.com )米 C. ( http: / / www.21cnjy.com )米 D.6tan75°米
4.(2017 苏州一模)如图,某高楼顶部 ( http: / / www.21cnjy.com )有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
( http: / / www.21cnjy.com )
A.(35 ( http: / / www.21cnjy.com )+55)m B.(25 ( http: / / www.21cnjy.com )+45)m C.(25 ( http: / / www.21cnjy.com )+75)m D.(50+20 ( http: / / www.21cnjy.com ))m
5.(2017 玉林)如图,一艘轮船在A处 ( http: / / www.21cnjy.com )测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )
( http: / / www.21cnjy.com )
A.15 ( http: / / www.21cnjy.com )海里 B.30海里 C.45海里 D.30 ( http: / / www.21cnjy.com )海里
6.(2017 临沂模拟) ( http: / / www.21cnjy.com )如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )海里 B. ( http: / / www.21cnjy.com )海里 C. ( http: / / www.21cnjy.com )海里 D. ( http: / / www.21cnjy.com )海里
7.(2017 相城区模拟)如图,小岛 ( http: / / www.21cnjy.com )在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向,则货船的航行速度是( )【出处:21教育名师】
( http: / / www.21cnjy.com )
A.7 ( http: / / www.21cnjy.com )海里/时 B.7 ( http: / / www.21cnjy.com )海里/时 C.7 ( http: / / www.21cnjy.com )海里/时 D.28 ( http: / / www.21cnjy.com )海里/时
8.(2016秋 金堂县校级期末) ( http: / / www.21cnjy.com )如图,小颖家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的400米处,那么水塔所在的位置到公路的距离AB是( )
( http: / / www.21cnjy.com )
A.200米 B.200 ( http: / / www.21cnjy.com )米 C. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )米 D.400 ( http: / / www.21cnjy.com )米
9.(2017春 南岗区校级期中) ( http: / / www.21cnjy.com )如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB距离PC为( )
( http: / / www.21cnjy.com )
A.3米 B. ( http: / / www.21cnjy.com )米 C.2米 D.1米
10.(2017 道里区校级模拟)如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC= ( http: / / www.21cnjy.com ),点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
( http: / / www.21cnjy.com )
A.200 ( http: / / www.21cnjy.com ) B.200 C.100 ( http: / / www.21cnjy.com ) D.100
二.填空题(每小题5分,共30分)
11.(2017 抚顺)如图,某城市的电视塔 ( http: / / www.21cnjy.com )AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为 米(结果保留根号).
( http: / / www.21cnjy.com )
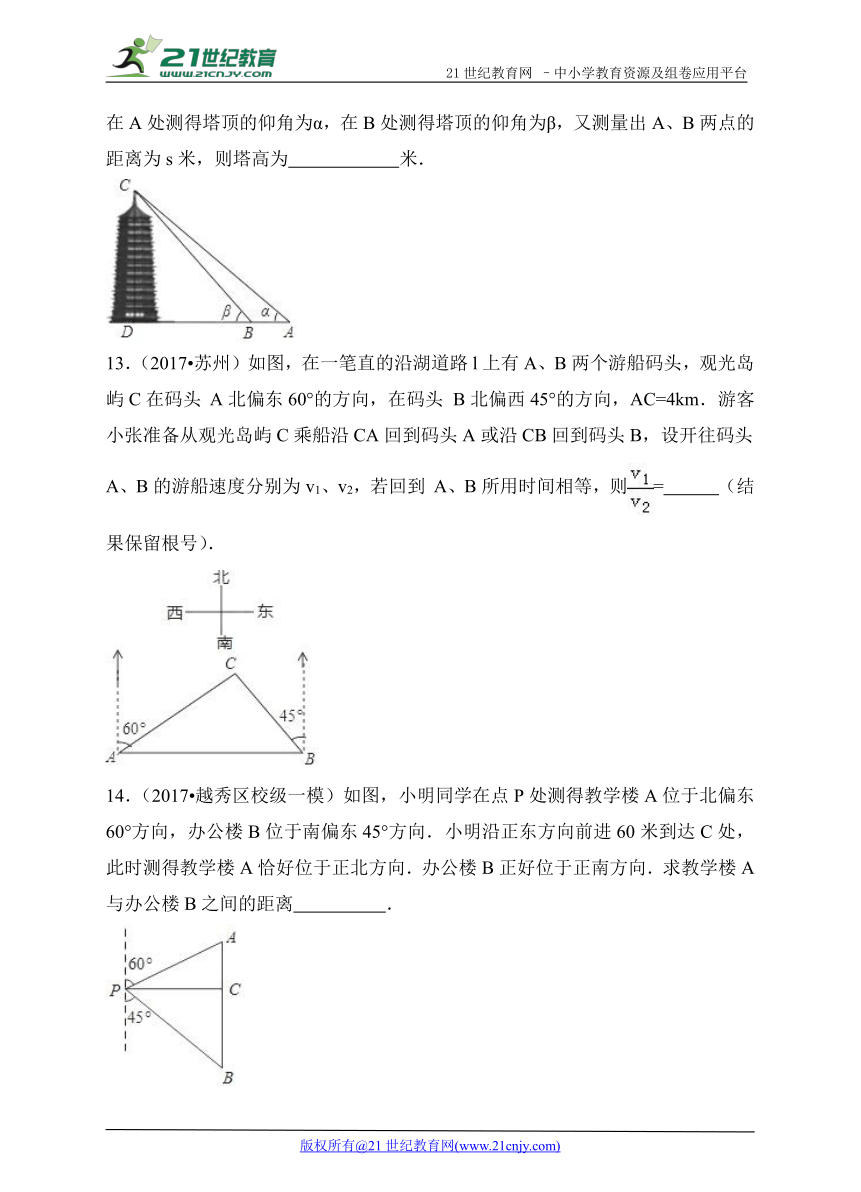
12.(2017 东营)一 ( http: / / www.21cnjy.com )数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为 米.www.21-cn-jy.com
( http: / / www.21cnjy.com )
13.(2017 苏州)如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则 ( http: / / www.21cnjy.com )= (结果保留根号).21*cnjy*com
( http: / / www.21cnjy.com )
14.(2017 越秀区 ( http: / / www.21cnjy.com )校级一模)如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离 .
( http: / / www.21cnjy.com )
15.(2016 十堰)在综合实践课上 ( http: / / www.21cnjy.com ),小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)
( http: / / www.21cnjy.com )
16.(2016 张家港市二模)在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度 米.(参考数据: ( http: / / www.21cnjy.com ))
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2017 黄冈)在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ( http: / / www.21cnjy.com )≈1.41, ( http: / / www.21cnjy.com )≈1.73)
( http: / / www.21cnjy.com )
18.(10分)(2017 营口)如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点A处测得码头C在船的东北方向,航行40分钟后到达B处,这时码头C恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头C的最近距离.(结果精确到0.1海里,参考数据 ( http: / / www.21cnjy.com )≈1.41, ( http: / / www.21cnjy.com )≈1.73)
( http: / / www.21cnjy.com )
1.6利用三角函数测高检测
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 重庆)如图,小王在长江 ( http: / / www.21cnjy.com )边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.5.1米 B.6.3米 C.7.1米 D.9.2米
【分析】延长DE交AB延长线于点P,作CQ⊥AP,可得CE=PQ=2、CQ=PE,由i= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )可设CQ=4x、BQ=3x,根据BQ2+CQ2=BC2求得x的值,即可知DP=11,由AP= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )结合AB=AP﹣BQ﹣PQ可得答案.
【解答】解:如图,延长DE交AB延长线于点P,作CQ⊥AP于点Q,
( http: / / www.21cnjy.com )
∵CE∥AP,
∴DP⊥AP,
∴四边形CEPQ为矩形,
∴CE=PQ=2,CQ=PE,
∵i= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴设CQ=4x、BQ=3x,
由BQ2+CQ2=BC2可得(4x)2+(3x)2=102,
解得:x=2或x=﹣2(舍),
则CQ=PE=8,BQ=6,
∴DP=DE+PE=11,
在Rt△ADP中,∵AP= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )≈13.1,
∴AB=AP﹣BQ﹣PQ=13.1﹣6﹣2=5.1,
故选:A.
2.(2017 烟台)如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ( http: / / www.21cnjy.com )≈1.414)( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.34.14米 B.34.1米 C.35.7米 D.35.74米
【分析】过B作BF⊥CD于F,作B′E⊥BD,解直角三角形即可得到结论.
【解答】解:过B作BF⊥CD于F,作B′E⊥BD,
∵∠BDB'=∠B'DC=22.5°,
∴EB'=B'C,
∵∠BEB′=45°,
∴EB′=B′F=10√2,
∴DF=20+10√2,
∴DC=DF+FC=20+10√2+1.6≈35.74=35.7,
故选C,
( http: / / www.21cnjy.com )
3.(2017 龙岗区一模)如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
( http: / / www.21cnjy.com )
A.6sin75°米 B. ( http: / / www.21cnjy.com )米 C. ( http: / / www.21cnjy.com )米 D.6tan75°米
【分析】根据题意可知BC⊥AC,在Rt△ABC中,AC=7米,∠BAC=α,利用三角函数即可求出BC的高度.
【解答】解:∵BC⊥AC,AC=7米,∠BAC=α,
∴ ( http: / / www.21cnjy.com )=tanα,
∴BC=AC tanα=6tanα(米).
故选;D.
4.(2017 苏州一模)如图,某 ( http: / / www.21cnjy.com )高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
( http: / / www.21cnjy.com )
A.(35 ( http: / / www.21cnjy.com )+55)m B.(25 ( http: / / www.21cnjy.com )+45)m C.(25 ( http: / / www.21cnjy.com )+75)m D.(50+20 ( http: / / www.21cnjy.com ))m
【分析】将题目中所涉及到的仰角转换为直角 ( http: / / www.21cnjy.com )三角形的内角,利用解直角三角形的知识表示出线段CG的长,根据三角函数值求得CG的长,代入FG=x tanβ即可求得.21教育名师原创作品
【解答】解:设CG=xm,
由图可知:EF=(x+20) tan45°,FG=x tan60°,
则(x+20)tan45°+30=xtan60°,
解得x= ( http: / / www.21cnjy.com )=25( ( http: / / www.21cnjy.com )+1),
则FG=x tan60°=25( ( http: / / www.21cnjy.com )+1)× ( http: / / www.21cnjy.com )=(75+25 ( http: / / www.21cnjy.com ))m.
故选C.
5.(2017 玉林)如图,一艘轮船 ( http: / / www.21cnjy.com )在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )
( http: / / www.21cnjy.com )
A.15 ( http: / / www.21cnjy.com )海里 B.30海里 C.45海里 D.30 ( http: / / www.21cnjy.com )海里
【分析】作CD⊥AB,垂足为D.构建直角三角形后,根据30°的角对的直角边是斜边的一半,求出BP.
【解答】解:作BD⊥AP,垂足为D
( http: / / www.21cnjy.com ).
根据题意,得∠BAD=30°,BD=15海里,
∴∠PBD=60°,
则∠DPB=30°,BP=15×2=30(海里),
故选:B.
6.(2017 临沂模拟)如图,某轮船 ( http: / / www.21cnjy.com )在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( )21教育网
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )海里 B. ( http: / / www.21cnjy.com )海里 C. ( http: / / www.21cnjy.com )海里 D. ( http: / / www.21cnjy.com )海里
【分析】作AC⊥OB于C点,根据题目提供的方向角,并从图中整理出直角三角形的模型,利用解直角三角形的知识求得BC的长即可.
【解答】解:作AC⊥OB于C点,只要到C处,轮船离电视塔最近,求出BC长即可,
由已知得:∠AOB=30°,∠ABC=45°、OB=20海里,
∴BC=AC,CO=AC÷tan∠AOB=AC÷tan30°= ( http: / / www.21cnjy.com ),
∵CO﹣CB= ( http: / / www.21cnjy.com )﹣AC=20,
解得:AC= ( http: / / www.21cnjy.com )海里,
∴BC=AC=10( ( http: / / www.21cnjy.com )+1)海里,
故选A.
( http: / / www.21cnjy.com )
7.(2017 相城区模拟)如 ( http: / / www.21cnjy.com )图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向,则货船的航行速度是( )21·cn·jy·com
( http: / / www.21cnjy.com )
A.7 ( http: / / www.21cnjy.com )海里/时 B.7 ( http: / / www.21cnjy.com )海里/时 C.7 ( http: / / www.21cnjy.com )海里/时 D.28 ( http: / / www.21cnjy.com )海里/时
【分析】由已知可得AB⊥PQ,∠QAP ( http: / / www.21cnjy.com )=60°,∠A=30°,AP=56海里,要求货船的航行速度,即是求PB的长,可先在直角三角形APQ中利用三角函数求出PQ,然后利用三角函数求出PB即可.
【解答】解:设货船的航行速度为x海里/时,4小时后货船在点B处,作PQ⊥AB于点Q.
由题意AP=56海里,PB=4x海里,
在直角三角形APQ中,∠APQ=60°,
所以PQ=28.
在直角三角形PQB中,∠BPQ=45°,
所以,PQ=PB×cos45°=2 ( http: / / www.21cnjy.com )x.
所以,2 ( http: / / www.21cnjy.com )x=28,
解得:x=7 ( http: / / www.21cnjy.com ).
故选:A.
( http: / / www.21cnjy.com )
8.(2016秋 金堂县校级期末)如图,小 ( http: / / www.21cnjy.com )颖家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的400米处,那么水塔所在的位置到公路的距离AB是( )
( http: / / www.21cnjy.com )
A.200米 B.200 ( http: / / www.21cnjy.com )米 C. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )米 D.400 ( http: / / www.21cnjy.com )米
【分析】在Rt△AOB中,由∠AOB=30°可知AB= ( http: / / www.21cnjy.com )AO,由此即可解决问题.
【解答】解:由题意∠AOB=90°﹣60°=30°,OA=400米,
∵AB⊥OB,
∴∠ABO=90°,
∴AB= ( http: / / www.21cnjy.com )AO=200米.
故选A.
( http: / / www.21cnjy.com )
9.(2017春 南岗区校级 ( http: / / www.21cnjy.com )期中)如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB距离PC为( )
( http: / / www.21cnjy.com )
A.3米 B. ( http: / / www.21cnjy.com )米 C.2米 D.1米
【分析】设点P到直线AB距离PC为x米,根据正切的定义用x表示出AC、BC,根据题意列出方程,解方程即可.21世纪教育网版权所有
【解答】解:设点P到直线AB距离PC为x米,
在Rt△APC中,AC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )x,
在Rt△BPC中,BC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )x,
由题意得, ( http: / / www.21cnjy.com )x﹣ ( http: / / www.21cnjy.com )x=2,
解得,x= ( http: / / www.21cnjy.com )(米),
故选:B.
10.(2017 道里区校级模拟)如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC= ( http: / / www.21cnjy.com ),点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
( http: / / www.21cnjy.com )
A.200 ( http: / / www.21cnjy.com ) B.200 C.100 ( http: / / www.21cnjy.com ) D.100
【分析】根据特殊角的正切值得到∠ABC=30°,得到∠PBA=90°,根据正弦的定义求出PB,根据正切的概念计算即可,
【解答】解:∵tan∠ABC= ( http: / / www.21cnjy.com ),
∴∠ABC=30°,
由题意得,∠PBH=60°,
∴∠PBA=90°,
在Rt△PBH中,PB= ( http: / / www.21cnjy.com )=200 ( http: / / www.21cnjy.com ),
在Rt△PBA中,AB=PB tan∠APB=200,
故选:B.
二.填空题(每小题5分,共30分)
11.(2017 抚顺)如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为 100 ( http: / / www.21cnjy.com ) 米(结果保留根号).
( http: / / www.21cnjy.com )
【分析】先求出∠ANB=45°,进而推得AN=MN,最后用等腰直角三角形的性质即可得出结论.
【解答】解:如图,
( http: / / www.21cnjy.com )
连接AN,由题意知,BM⊥AA',BA=BA'
∴AN=A'N,
∴∠ANB=∠A'NB=45°,
∵∠AMB=22.5°,
∴∠MAN=∠ANB﹣∠AMB=22.5°=∠AMN,
∴AN=MN=200米,
在Rt△ABN中,∠ANB=45°,
∴AB= ( http: / / www.21cnjy.com )AN=100 ( http: / / www.21cnjy.com )(米),
故答案为100 ( http: / / www.21cnjy.com ).
12.(2017 东营)一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为 ( http: / / www.21cnjy.com ) 米.2·1·c·n·j·y
( http: / / www.21cnjy.com )
【分析】在Rt△BCD中有BD= ( http: / / www.21cnjy.com ),在Rt△ACD中,根据tan∠A= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )可得tanα= ( http: / / www.21cnjy.com ),解之求出CD即可得.
【解答】解:在Rt△BCD中,∵tan∠CBD= ( http: / / www.21cnjy.com ),
∴BD= ( http: / / www.21cnjy.com ),
在Rt△ACD中,∵tan∠A= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴tanα= ( http: / / www.21cnjy.com ),
解得:CD= ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com ).
13.(2017 苏州)如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ) (结果保留根号).
( http: / / www.21cnjy.com )
【分析】作CD⊥AB于点D,在Rt△ACD中利用三角函数求得CD的长,然后在Rt△BCD中求得BC的长,然后根据 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )求解.
【解答】解:作CD⊥AB于点B.
∵在Rt△ACD中,∠CAD=90°﹣60°=30°,
∴CD=AC sin∠CAD=4× ( http: / / www.21cnjy.com )=2(km),
∵Rt△BCD中,∠CBD=90°,
∴BC= ( http: / / www.21cnjy.com )CD=2 ( http: / / www.21cnjy.com )(km),
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故答案是: ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
14.(2017 越秀区校级一模)如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离 (60+20 ( http: / / www.21cnjy.com ))米 .
( http: / / www.21cnjy.com )
【分析】由已知可得△ABP中∠A=60 ( http: / / www.21cnjy.com )°∠B=45°且PC=60m,要求AB的长,可以先求出AC和BC的长就可转化为运用三角函数解直角三角形.
【解答】解:由题意可知:
∠ACP=∠BCP=90°,∠APC=30°,∠BPC=45°.
在Rt△BPC中,
∵∠BCP=90°,∠B=∠BPC=45°,
∴BC=PC=60.
在Rt△ACP中,
∵∠ACP=90°,∠APC=30°,
tan30°= ( http: / / www.21cnjy.com ),
∴AC=PC tan30°=tan30°×60=60× ( http: / / www.21cnjy.com )=20 ( http: / / www.21cnjy.com )(米).
∴AB=AC+BC=60+20 ( http: / / www.21cnjy.com )(米).
答:教学楼A与办公楼B之间的距离是(60+20 ( http: / / www.21cnjy.com ))米.
故答案是:(60+20 ( http: / / www.21cnjy.com ))米.
( http: / / www.21cnjy.com )
15.(2016 十堰)在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 (30+10 ( http: / / www.21cnjy.com )) 米.(结果保留根号)www-2-1-cnjy-com
( http: / / www.21cnjy.com )
【分析】如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,设CK=HB=x,根据tan30°= ( http: / / www.21cnjy.com )列出方程即可解决问题.
【解答】解:如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,
( http: / / www.21cnjy.com )
设CK=HB=x,
∵∠CKA=90°,∠CAK=45°,
∴∠CAK=∠ACK=45°,
∴AK=CK=x,BK=HC=AK﹣AB=x﹣30,
∴HD=x﹣30+10=x﹣20,
在RT△BHD中,∵∠BHD=90°,∠HBD=30°,
∴tan30°= ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
解得x=30+10 ( http: / / www.21cnjy.com ).
∴河的宽度为(30+10 ( http: / / www.21cnjy.com ))米.
16.(2016 张家港市二模)在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度 30 米.(参考数据: ( http: / / www.21cnjy.com ))
( http: / / www.21cnjy.com )
【分析】作CE⊥AB于E,设CE=x,在RT△ACE中,根据tan∠CAE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )列出方程即可解决问题.21cnjy.com
【解答】解:如图,作CE⊥AB于E,
设CE=x,
由题意得∠CBE=45°,∠CAE=31°,
∴∠CBE=∠BCE=45°,
∴CE=BE=x,AE=20+x,
∵tan31°= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴x=30,
∴CE=30米.
故答案为30.
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2017 黄冈)在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ( http: / / www.21cnjy.com )≈1.41, ( http: / / www.21cnjy.com )≈1.73)21·世纪*教育网
( http: / / www.21cnjy.com )
【分析】如图作FH⊥AE于H.由题意可知∠HAF=∠HFA=45°,推出AH=HF,设AH=HF=x,则EF=2x,EH= ( http: / / www.21cnjy.com )x,在Rt△AEB中,由∠E=30°,AB=5米,推出AE=2AB=10米,可得x+ ( http: / / www.21cnjy.com )x=10,解方程即可.2-1-c-n-j-y
【解答】解:如图作FH⊥AE于H.由题意可知∠HAF=∠HFA=45°,
∴AH=HF,设AH=HF=x,则EF=2x,EH= ( http: / / www.21cnjy.com )x,
在Rt△AEB中,∵∠E=30°,AB=5米,
∴AE=2AB=10米,
∴x+ ( http: / / www.21cnjy.com )x=10,
∴x=5 ( http: / / www.21cnjy.com )﹣5,
∴EF=2x=10 ( http: / / www.21cnjy.com )﹣10≈7.3米,
答:E与点F之间的距离为7.3米.
( http: / / www.21cnjy.com )
18.(10分)(2017 营口)如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点A处测得码头C在船的东北方向,航行40分钟后到达B处,这时码头C恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头C的最近距离.(结果精确到0.1海里,参考数据 ( http: / / www.21cnjy.com )≈1.41, ( http: / / www.21cnjy.com )≈1.73)
( http: / / www.21cnjy.com )
【分析】过点C作CE⊥AB于点E,过点 ( http: / / www.21cnjy.com )B作BD⊥AC于点D,由题意可知:船在航行过程中与码头C的最近距离是CE,根据∠DAB=30°,AB=20,从而可求出BD、AD的长度,进而可求出CE的长度.【版权所有:21教育】
【解答】解:过点C作CE⊥AB于点E,过点B作BD⊥AC于点D,
由题意可知:船在航行过程中与码头C的最近距离是CE,
AB=30× ( http: / / www.21cnjy.com )=20,
∵∠NAC=45°,∠NAB=75°,
∴∠DAB=30°,
∴BD= ( http: / / www.21cnjy.com )AB=10,
由勾股定理可知:AD=10 ( http: / / www.21cnjy.com )
∵BC∥AN,
∴∠BCD=45°,
∴CD=BD=10,
∴AC=10 ( http: / / www.21cnjy.com )+10
∵∠DAB=30°,
∴CE= ( http: / / www.21cnjy.com )AC=5 ( http: / / www.21cnjy.com )+5≈13.7
答:船在航行过程中与码头C的最近距离是13.7海里
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
1.6利用三角函数测高检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017 重庆)如图,小王在长江边 ( http: / / www.21cnjy.com )某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).21*cnjy*com
( http: / / www.21cnjy.com )
A.5.1米 B.6.3米 C.7.1米 D.9.2米
2.(2017 烟台)如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ( http: / / www.21cnjy.com )≈1.414)( )
( http: / / www.21cnjy.com )
A.34.14米 B.34.1米 C.35.7米 D.35.74米
3.(2017 龙岗区一模)如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
( http: / / www.21cnjy.com )
A.6sin75°米 B. ( http: / / www.21cnjy.com )米 C. ( http: / / www.21cnjy.com )米 D.6tan75°米
4.(2017 苏州一模)如图,某高楼顶部 ( http: / / www.21cnjy.com )有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
( http: / / www.21cnjy.com )
A.(35 ( http: / / www.21cnjy.com )+55)m B.(25 ( http: / / www.21cnjy.com )+45)m C.(25 ( http: / / www.21cnjy.com )+75)m D.(50+20 ( http: / / www.21cnjy.com ))m
5.(2017 玉林)如图,一艘轮船在A处 ( http: / / www.21cnjy.com )测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )
( http: / / www.21cnjy.com )
A.15 ( http: / / www.21cnjy.com )海里 B.30海里 C.45海里 D.30 ( http: / / www.21cnjy.com )海里
6.(2017 临沂模拟) ( http: / / www.21cnjy.com )如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )海里 B. ( http: / / www.21cnjy.com )海里 C. ( http: / / www.21cnjy.com )海里 D. ( http: / / www.21cnjy.com )海里
7.(2017 相城区模拟)如图,小岛 ( http: / / www.21cnjy.com )在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向,则货船的航行速度是( )【出处:21教育名师】
( http: / / www.21cnjy.com )
A.7 ( http: / / www.21cnjy.com )海里/时 B.7 ( http: / / www.21cnjy.com )海里/时 C.7 ( http: / / www.21cnjy.com )海里/时 D.28 ( http: / / www.21cnjy.com )海里/时
8.(2016秋 金堂县校级期末) ( http: / / www.21cnjy.com )如图,小颖家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的400米处,那么水塔所在的位置到公路的距离AB是( )
( http: / / www.21cnjy.com )
A.200米 B.200 ( http: / / www.21cnjy.com )米 C. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )米 D.400 ( http: / / www.21cnjy.com )米
9.(2017春 南岗区校级期中) ( http: / / www.21cnjy.com )如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB距离PC为( )
( http: / / www.21cnjy.com )
A.3米 B. ( http: / / www.21cnjy.com )米 C.2米 D.1米
10.(2017 道里区校级模拟)如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC= ( http: / / www.21cnjy.com ),点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
( http: / / www.21cnjy.com )
A.200 ( http: / / www.21cnjy.com ) B.200 C.100 ( http: / / www.21cnjy.com ) D.100
二.填空题(每小题5分,共30分)
11.(2017 抚顺)如图,某城市的电视塔 ( http: / / www.21cnjy.com )AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为 米(结果保留根号).
( http: / / www.21cnjy.com )
12.(2017 东营)一 ( http: / / www.21cnjy.com )数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为 米.www.21-cn-jy.com
( http: / / www.21cnjy.com )
13.(2017 苏州)如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则 ( http: / / www.21cnjy.com )= (结果保留根号).21*cnjy*com
( http: / / www.21cnjy.com )
14.(2017 越秀区 ( http: / / www.21cnjy.com )校级一模)如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离 .
( http: / / www.21cnjy.com )
15.(2016 十堰)在综合实践课上 ( http: / / www.21cnjy.com ),小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)
( http: / / www.21cnjy.com )
16.(2016 张家港市二模)在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度 米.(参考数据: ( http: / / www.21cnjy.com ))
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2017 黄冈)在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ( http: / / www.21cnjy.com )≈1.41, ( http: / / www.21cnjy.com )≈1.73)
( http: / / www.21cnjy.com )
18.(10分)(2017 营口)如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点A处测得码头C在船的东北方向,航行40分钟后到达B处,这时码头C恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头C的最近距离.(结果精确到0.1海里,参考数据 ( http: / / www.21cnjy.com )≈1.41, ( http: / / www.21cnjy.com )≈1.73)
( http: / / www.21cnjy.com )
1.6利用三角函数测高检测
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 重庆)如图,小王在长江 ( http: / / www.21cnjy.com )边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.5.1米 B.6.3米 C.7.1米 D.9.2米
【分析】延长DE交AB延长线于点P,作CQ⊥AP,可得CE=PQ=2、CQ=PE,由i= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )可设CQ=4x、BQ=3x,根据BQ2+CQ2=BC2求得x的值,即可知DP=11,由AP= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )结合AB=AP﹣BQ﹣PQ可得答案.
【解答】解:如图,延长DE交AB延长线于点P,作CQ⊥AP于点Q,
( http: / / www.21cnjy.com )
∵CE∥AP,
∴DP⊥AP,
∴四边形CEPQ为矩形,
∴CE=PQ=2,CQ=PE,
∵i= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴设CQ=4x、BQ=3x,
由BQ2+CQ2=BC2可得(4x)2+(3x)2=102,
解得:x=2或x=﹣2(舍),
则CQ=PE=8,BQ=6,
∴DP=DE+PE=11,
在Rt△ADP中,∵AP= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )≈13.1,
∴AB=AP﹣BQ﹣PQ=13.1﹣6﹣2=5.1,
故选:A.
2.(2017 烟台)如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ( http: / / www.21cnjy.com )≈1.414)( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.34.14米 B.34.1米 C.35.7米 D.35.74米
【分析】过B作BF⊥CD于F,作B′E⊥BD,解直角三角形即可得到结论.
【解答】解:过B作BF⊥CD于F,作B′E⊥BD,
∵∠BDB'=∠B'DC=22.5°,
∴EB'=B'C,
∵∠BEB′=45°,
∴EB′=B′F=10√2,
∴DF=20+10√2,
∴DC=DF+FC=20+10√2+1.6≈35.74=35.7,
故选C,
( http: / / www.21cnjy.com )
3.(2017 龙岗区一模)如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
( http: / / www.21cnjy.com )
A.6sin75°米 B. ( http: / / www.21cnjy.com )米 C. ( http: / / www.21cnjy.com )米 D.6tan75°米
【分析】根据题意可知BC⊥AC,在Rt△ABC中,AC=7米,∠BAC=α,利用三角函数即可求出BC的高度.
【解答】解:∵BC⊥AC,AC=7米,∠BAC=α,
∴ ( http: / / www.21cnjy.com )=tanα,
∴BC=AC tanα=6tanα(米).
故选;D.
4.(2017 苏州一模)如图,某 ( http: / / www.21cnjy.com )高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
( http: / / www.21cnjy.com )
A.(35 ( http: / / www.21cnjy.com )+55)m B.(25 ( http: / / www.21cnjy.com )+45)m C.(25 ( http: / / www.21cnjy.com )+75)m D.(50+20 ( http: / / www.21cnjy.com ))m
【分析】将题目中所涉及到的仰角转换为直角 ( http: / / www.21cnjy.com )三角形的内角,利用解直角三角形的知识表示出线段CG的长,根据三角函数值求得CG的长,代入FG=x tanβ即可求得.21教育名师原创作品
【解答】解:设CG=xm,
由图可知:EF=(x+20) tan45°,FG=x tan60°,
则(x+20)tan45°+30=xtan60°,
解得x= ( http: / / www.21cnjy.com )=25( ( http: / / www.21cnjy.com )+1),
则FG=x tan60°=25( ( http: / / www.21cnjy.com )+1)× ( http: / / www.21cnjy.com )=(75+25 ( http: / / www.21cnjy.com ))m.
故选C.
5.(2017 玉林)如图,一艘轮船 ( http: / / www.21cnjy.com )在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )
( http: / / www.21cnjy.com )
A.15 ( http: / / www.21cnjy.com )海里 B.30海里 C.45海里 D.30 ( http: / / www.21cnjy.com )海里
【分析】作CD⊥AB,垂足为D.构建直角三角形后,根据30°的角对的直角边是斜边的一半,求出BP.
【解答】解:作BD⊥AP,垂足为D
( http: / / www.21cnjy.com ).
根据题意,得∠BAD=30°,BD=15海里,
∴∠PBD=60°,
则∠DPB=30°,BP=15×2=30(海里),
故选:B.
6.(2017 临沂模拟)如图,某轮船 ( http: / / www.21cnjy.com )在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行( )21教育网
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com )海里 B. ( http: / / www.21cnjy.com )海里 C. ( http: / / www.21cnjy.com )海里 D. ( http: / / www.21cnjy.com )海里
【分析】作AC⊥OB于C点,根据题目提供的方向角,并从图中整理出直角三角形的模型,利用解直角三角形的知识求得BC的长即可.
【解答】解:作AC⊥OB于C点,只要到C处,轮船离电视塔最近,求出BC长即可,
由已知得:∠AOB=30°,∠ABC=45°、OB=20海里,
∴BC=AC,CO=AC÷tan∠AOB=AC÷tan30°= ( http: / / www.21cnjy.com ),
∵CO﹣CB= ( http: / / www.21cnjy.com )﹣AC=20,
解得:AC= ( http: / / www.21cnjy.com )海里,
∴BC=AC=10( ( http: / / www.21cnjy.com )+1)海里,
故选A.
( http: / / www.21cnjy.com )
7.(2017 相城区模拟)如 ( http: / / www.21cnjy.com )图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向,则货船的航行速度是( )21·cn·jy·com
( http: / / www.21cnjy.com )
A.7 ( http: / / www.21cnjy.com )海里/时 B.7 ( http: / / www.21cnjy.com )海里/时 C.7 ( http: / / www.21cnjy.com )海里/时 D.28 ( http: / / www.21cnjy.com )海里/时
【分析】由已知可得AB⊥PQ,∠QAP ( http: / / www.21cnjy.com )=60°,∠A=30°,AP=56海里,要求货船的航行速度,即是求PB的长,可先在直角三角形APQ中利用三角函数求出PQ,然后利用三角函数求出PB即可.
【解答】解:设货船的航行速度为x海里/时,4小时后货船在点B处,作PQ⊥AB于点Q.
由题意AP=56海里,PB=4x海里,
在直角三角形APQ中,∠APQ=60°,
所以PQ=28.
在直角三角形PQB中,∠BPQ=45°,
所以,PQ=PB×cos45°=2 ( http: / / www.21cnjy.com )x.
所以,2 ( http: / / www.21cnjy.com )x=28,
解得:x=7 ( http: / / www.21cnjy.com ).
故选:A.
( http: / / www.21cnjy.com )
8.(2016秋 金堂县校级期末)如图,小 ( http: / / www.21cnjy.com )颖家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的400米处,那么水塔所在的位置到公路的距离AB是( )
( http: / / www.21cnjy.com )
A.200米 B.200 ( http: / / www.21cnjy.com )米 C. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )米 D.400 ( http: / / www.21cnjy.com )米
【分析】在Rt△AOB中,由∠AOB=30°可知AB= ( http: / / www.21cnjy.com )AO,由此即可解决问题.
【解答】解:由题意∠AOB=90°﹣60°=30°,OA=400米,
∵AB⊥OB,
∴∠ABO=90°,
∴AB= ( http: / / www.21cnjy.com )AO=200米.
故选A.
( http: / / www.21cnjy.com )
9.(2017春 南岗区校级 ( http: / / www.21cnjy.com )期中)如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB距离PC为( )
( http: / / www.21cnjy.com )
A.3米 B. ( http: / / www.21cnjy.com )米 C.2米 D.1米
【分析】设点P到直线AB距离PC为x米,根据正切的定义用x表示出AC、BC,根据题意列出方程,解方程即可.21世纪教育网版权所有
【解答】解:设点P到直线AB距离PC为x米,
在Rt△APC中,AC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )x,
在Rt△BPC中,BC= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )x,
由题意得, ( http: / / www.21cnjy.com )x﹣ ( http: / / www.21cnjy.com )x=2,
解得,x= ( http: / / www.21cnjy.com )(米),
故选:B.
10.(2017 道里区校级模拟)如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC= ( http: / / www.21cnjy.com ),点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
( http: / / www.21cnjy.com )
A.200 ( http: / / www.21cnjy.com ) B.200 C.100 ( http: / / www.21cnjy.com ) D.100
【分析】根据特殊角的正切值得到∠ABC=30°,得到∠PBA=90°,根据正弦的定义求出PB,根据正切的概念计算即可,
【解答】解:∵tan∠ABC= ( http: / / www.21cnjy.com ),
∴∠ABC=30°,
由题意得,∠PBH=60°,
∴∠PBA=90°,
在Rt△PBH中,PB= ( http: / / www.21cnjy.com )=200 ( http: / / www.21cnjy.com ),
在Rt△PBA中,AB=PB tan∠APB=200,
故选:B.
二.填空题(每小题5分,共30分)
11.(2017 抚顺)如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为 100 ( http: / / www.21cnjy.com ) 米(结果保留根号).
( http: / / www.21cnjy.com )
【分析】先求出∠ANB=45°,进而推得AN=MN,最后用等腰直角三角形的性质即可得出结论.
【解答】解:如图,
( http: / / www.21cnjy.com )
连接AN,由题意知,BM⊥AA',BA=BA'
∴AN=A'N,
∴∠ANB=∠A'NB=45°,
∵∠AMB=22.5°,
∴∠MAN=∠ANB﹣∠AMB=22.5°=∠AMN,
∴AN=MN=200米,
在Rt△ABN中,∠ANB=45°,
∴AB= ( http: / / www.21cnjy.com )AN=100 ( http: / / www.21cnjy.com )(米),
故答案为100 ( http: / / www.21cnjy.com ).
12.(2017 东营)一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为 ( http: / / www.21cnjy.com ) 米.2·1·c·n·j·y
( http: / / www.21cnjy.com )
【分析】在Rt△BCD中有BD= ( http: / / www.21cnjy.com ),在Rt△ACD中,根据tan∠A= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )可得tanα= ( http: / / www.21cnjy.com ),解之求出CD即可得.
【解答】解:在Rt△BCD中,∵tan∠CBD= ( http: / / www.21cnjy.com ),
∴BD= ( http: / / www.21cnjy.com ),
在Rt△ACD中,∵tan∠A= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴tanα= ( http: / / www.21cnjy.com ),
解得:CD= ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com ).
13.(2017 苏州)如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ) (结果保留根号).
( http: / / www.21cnjy.com )
【分析】作CD⊥AB于点D,在Rt△ACD中利用三角函数求得CD的长,然后在Rt△BCD中求得BC的长,然后根据 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )求解.
【解答】解:作CD⊥AB于点B.
∵在Rt△ACD中,∠CAD=90°﹣60°=30°,
∴CD=AC sin∠CAD=4× ( http: / / www.21cnjy.com )=2(km),
∵Rt△BCD中,∠CBD=90°,
∴BC= ( http: / / www.21cnjy.com )CD=2 ( http: / / www.21cnjy.com )(km),
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ).
故答案是: ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
14.(2017 越秀区校级一模)如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离 (60+20 ( http: / / www.21cnjy.com ))米 .
( http: / / www.21cnjy.com )
【分析】由已知可得△ABP中∠A=60 ( http: / / www.21cnjy.com )°∠B=45°且PC=60m,要求AB的长,可以先求出AC和BC的长就可转化为运用三角函数解直角三角形.
【解答】解:由题意可知:
∠ACP=∠BCP=90°,∠APC=30°,∠BPC=45°.
在Rt△BPC中,
∵∠BCP=90°,∠B=∠BPC=45°,
∴BC=PC=60.
在Rt△ACP中,
∵∠ACP=90°,∠APC=30°,
tan30°= ( http: / / www.21cnjy.com ),
∴AC=PC tan30°=tan30°×60=60× ( http: / / www.21cnjy.com )=20 ( http: / / www.21cnjy.com )(米).
∴AB=AC+BC=60+20 ( http: / / www.21cnjy.com )(米).
答:教学楼A与办公楼B之间的距离是(60+20 ( http: / / www.21cnjy.com ))米.
故答案是:(60+20 ( http: / / www.21cnjy.com ))米.
( http: / / www.21cnjy.com )
15.(2016 十堰)在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 (30+10 ( http: / / www.21cnjy.com )) 米.(结果保留根号)www-2-1-cnjy-com
( http: / / www.21cnjy.com )
【分析】如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,设CK=HB=x,根据tan30°= ( http: / / www.21cnjy.com )列出方程即可解决问题.
【解答】解:如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,
( http: / / www.21cnjy.com )
设CK=HB=x,
∵∠CKA=90°,∠CAK=45°,
∴∠CAK=∠ACK=45°,
∴AK=CK=x,BK=HC=AK﹣AB=x﹣30,
∴HD=x﹣30+10=x﹣20,
在RT△BHD中,∵∠BHD=90°,∠HBD=30°,
∴tan30°= ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
解得x=30+10 ( http: / / www.21cnjy.com ).
∴河的宽度为(30+10 ( http: / / www.21cnjy.com ))米.
16.(2016 张家港市二模)在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度 30 米.(参考数据: ( http: / / www.21cnjy.com ))
( http: / / www.21cnjy.com )
【分析】作CE⊥AB于E,设CE=x,在RT△ACE中,根据tan∠CAE= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )列出方程即可解决问题.21cnjy.com
【解答】解:如图,作CE⊥AB于E,
设CE=x,
由题意得∠CBE=45°,∠CAE=31°,
∴∠CBE=∠BCE=45°,
∴CE=BE=x,AE=20+x,
∵tan31°= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴x=30,
∴CE=30米.
故答案为30.
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2017 黄冈)在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ( http: / / www.21cnjy.com )≈1.41, ( http: / / www.21cnjy.com )≈1.73)21·世纪*教育网
( http: / / www.21cnjy.com )
【分析】如图作FH⊥AE于H.由题意可知∠HAF=∠HFA=45°,推出AH=HF,设AH=HF=x,则EF=2x,EH= ( http: / / www.21cnjy.com )x,在Rt△AEB中,由∠E=30°,AB=5米,推出AE=2AB=10米,可得x+ ( http: / / www.21cnjy.com )x=10,解方程即可.2-1-c-n-j-y
【解答】解:如图作FH⊥AE于H.由题意可知∠HAF=∠HFA=45°,
∴AH=HF,设AH=HF=x,则EF=2x,EH= ( http: / / www.21cnjy.com )x,
在Rt△AEB中,∵∠E=30°,AB=5米,
∴AE=2AB=10米,
∴x+ ( http: / / www.21cnjy.com )x=10,
∴x=5 ( http: / / www.21cnjy.com )﹣5,
∴EF=2x=10 ( http: / / www.21cnjy.com )﹣10≈7.3米,
答:E与点F之间的距离为7.3米.
( http: / / www.21cnjy.com )
18.(10分)(2017 营口)如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点A处测得码头C在船的东北方向,航行40分钟后到达B处,这时码头C恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头C的最近距离.(结果精确到0.1海里,参考数据 ( http: / / www.21cnjy.com )≈1.41, ( http: / / www.21cnjy.com )≈1.73)
( http: / / www.21cnjy.com )
【分析】过点C作CE⊥AB于点E,过点 ( http: / / www.21cnjy.com )B作BD⊥AC于点D,由题意可知:船在航行过程中与码头C的最近距离是CE,根据∠DAB=30°,AB=20,从而可求出BD、AD的长度,进而可求出CE的长度.【版权所有:21教育】
【解答】解:过点C作CE⊥AB于点E,过点B作BD⊥AC于点D,
由题意可知:船在航行过程中与码头C的最近距离是CE,
AB=30× ( http: / / www.21cnjy.com )=20,
∵∠NAC=45°,∠NAB=75°,
∴∠DAB=30°,
∴BD= ( http: / / www.21cnjy.com )AB=10,
由勾股定理可知:AD=10 ( http: / / www.21cnjy.com )
∵BC∥AN,
∴∠BCD=45°,
∴CD=BD=10,
∴AC=10 ( http: / / www.21cnjy.com )+10
∵∠DAB=30°,
∴CE= ( http: / / www.21cnjy.com )AC=5 ( http: / / www.21cnjy.com )+5≈13.7
答:船在航行过程中与码头C的最近距离是13.7海里
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
