2.2 二次函数的图象与性质(4)一课一测
文档属性
| 名称 | 2.2 二次函数的图象与性质(4)一课一测 |  | |
| 格式 | doc | ||
| 文件大小 | 648.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-22 10:23:50 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
2.2 二次函数的图象与性质
第四课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017 弥勒市二模)已知函数y=ax2+bx+c的图象如图所示,则函数y=ax+b的图象是( )www.21-cn-jy.com
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.(2017 胶州市一模)一次函数y=ax+b(a≠0)与二次函数y=ax2+2x+b(a≠0)在同一直角坐标系中的图象可能是( )www-2-1-cnjy-com
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
3.(2017 宁波)抛物线y=x2﹣2x+m2+2(m是常数)的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2017 陕西)已知抛物线y=x2 ( http: / / www.21cnjy.com )﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )
A.(1,﹣5) B.(3,﹣13) C.(2,﹣8) D.(4,﹣20)
5.(2017 河北区模拟)二次函数y=x2﹣4x﹣4的顶点坐标为( )
A.(2,﹣8) B.(2,8) C.(﹣2,8) D.(﹣2,﹣8)
6.(2017 包头三模)二次函数y=mx2﹣nx﹣2过点(1,0),且函数图象的顶点在第三象限,当m+n为整数时,则mn的值为( )【版权所有:21教育】
A.﹣ ( http: / / www.21cnjy.com ),﹣1 B.﹣ ( http: / / www.21cnjy.com ),﹣2 C.﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),﹣2 D. ( http: / / www.21cnjy.com ),﹣2
7.(2017 苏州一模)抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且经过点(3,0),则a﹣b+c的值为( )21*cnjy*com
A.﹣1 B.0 C.1 D.2
8.(2017秋 上杭县期中)已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.其中正确的结论的有( )
( http: / / www.21cnjy.com )
A.2个 B.3个 C.4个 D.5个
9.(2017 攀枝花)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列命题中正确的是( )
( http: / / www.21cnjy.com )
A.a>b>c
B.一次函数y=ax+c的图象不经第四象限
C.m(am+b)+b<a(m是任意实数)
D.3b+2c>0
10.(2017 澧县三模)若抛物线y=x2﹣2x+m的最低点的纵坐标为n,则m﹣n的值是( )
A.﹣1 B.0 C.1 D.2
二.填空题(每小题5分,共30分)
11.(2017 兰州)如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为 .
( http: / / www.21cnjy.com )
12.(2017 广陵区校级一模)如果抛物线y=﹣2x2+bx+3的对称轴是x=1,那么b= .
13.(2017 青浦区二模)抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是 .
14.(2017 台安县模拟)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ( http: / / www.21cnjy.com ),y2)是抛物线上两点,则y1>y2.其中说法正确的是 .
( http: / / www.21cnjy.com )
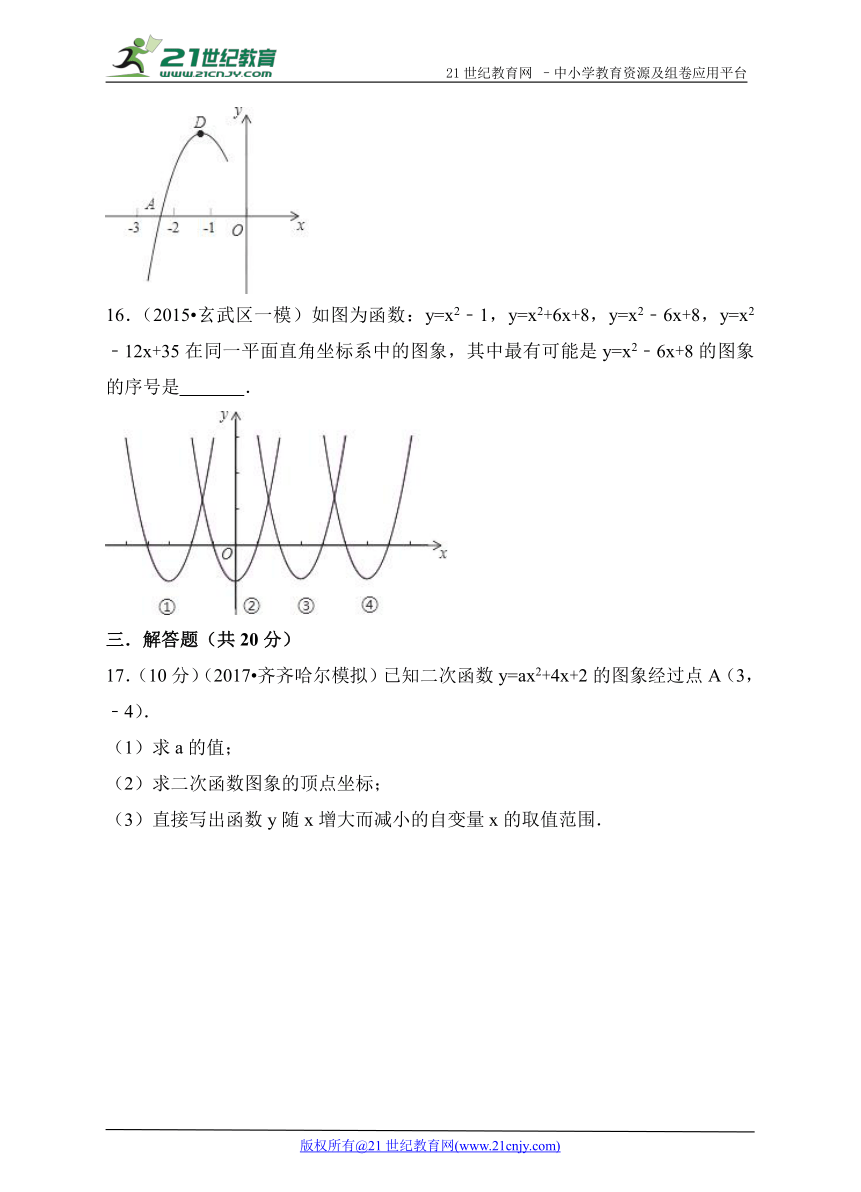
15.(2017 孝感模拟)抛物线y=ax ( http: / / www.21cnjy.com )2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有 (填序号).
( http: / / www.21cnjy.com )
16.(2015 玄武区一模)如图为函数: ( http: / / www.21cnjy.com )y=x2﹣1,y=x2+6x+8,y=x2﹣6x+8,y=x2﹣12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2﹣6x+8的图象的序号是 .
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2017 齐齐哈尔模拟)已知二次函数y=ax2+4x+2的图象经过点A(3,﹣4).
(1)求a的值;
(2)求二次函数图象的顶点坐标;
(3)直接写出函数y随x增大而减小的自变量x的取值范围.
18.(10分)(2017春 邳州市校级月考)在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣3(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)若线段AB上有且只有5个点的横坐标为整数,求m的取值范围;
(3)若抛物线在﹣1<x<0位于x轴下方,在3<x<4位于x轴上方,求m的值.
( http: / / www.21cnjy.com )
2.2 二次函数的图象与性质
第四课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 弥勒市二模)已知函数y=ax2+bx+c的图象如图所示,则函数y=ax+b的图象是( )21教育名师原创作品
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据抛物线开口向下确定出a<0,再根据对称轴确定出b,然后根据一次函数的性质确定出函数图象即可得解.
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=﹣ ( http: / / www.21cnjy.com )>0,
∴b>0,
∴函数y=ax+b的图象经过第二四象限且与y轴正半轴相交,
故选B.
2.(2017 胶州市一模)一次函数y=ax+b(a≠0)与二次函数y=ax2+2x+b(a≠0)在同一直角坐标系中的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】本题可先由一次函数y=ax+b图象得到字母系数的正负,再与二次函数y=ax2+2x+b的图象相比较看是否一致.
【解答】解:A、由抛物线可知,a>0,得b>0,由直线可知,a<0,b>0,故本选项错误;
B、由抛物线可知,a<0,b>0,由直线可知,a>0,b<0,故本选项错误;
C、由抛物线可知,a<0,b>0,由直线可知,a<0,b<0,故本选项错误;
D、由抛物线可知,a>0,b>0,由直线可知,a>0,b>0,且交y轴同一点,故本选项正确.
故选D.
3.(2017 宁波)抛物线y=x2﹣2x+m2+2(m是常数)的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】先根据抛物线的顶点式求出抛物线y=x2﹣2x+m2+2(m是常数)的顶点坐标,再根据各象限内点的坐标特点进行解答.
【解答】解:∵y=x2﹣2x+m2+2=(x﹣1)2+(m2+1),
∴顶点坐标为:(1,m2+1),
∵1>0,m2+1>0,
∴顶点在第一象限.
故选A.
4.(2017 陕西)已知 ( http: / / www.21cnjy.com )抛物线y=x2﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )
A.(1,﹣5) B.(3,﹣13) C.(2,﹣8) D.(4,﹣20)
【分析】先利用配方法求得点M的坐标,然后利用关于原点对称点的特点得到点M′的坐标,然后将点M′的坐标代入抛物线的解析式求解即可.
【解答】解:y=x2﹣2mx﹣4=x2﹣2mx+m2﹣m2﹣4=(x﹣m)2﹣m2﹣4.
∴点M(m,﹣m2﹣4).
∴点M′(﹣m,m2+4).
∴m2+2m2﹣4=m2+4.
解得m=±2.
∵m>0,
∴m=2.
∴M(2,﹣8).
故选C.
5.(2017 河北区模拟)二次函数y=x2﹣4x﹣4的顶点坐标为( )
A.(2,﹣8) B.(2,8) C.(﹣2,8) D.(﹣2,﹣8)
【分析】把二次函数化成顶点式,可得出二次函数的顶点坐标.
【解答】解:∵y=x2﹣4x﹣4=(x﹣2)2﹣8,
∴其顶点坐标为(2,﹣8),
故选A.
6.(2017 包头三模)二次函数y=mx2﹣nx﹣2过点(1,0),且函数图象的顶点在第三象限,当m+n为整数时,则mn的值为( )21·cn·jy·com
A.﹣ ( http: / / www.21cnjy.com ),﹣1 B.﹣ ( http: / / www.21cnjy.com ),﹣2 C.﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),﹣2 D. ( http: / / www.21cnjy.com ),﹣2
【分析】首先根据题意确定m、n的符号,然后进一步确定m的取值范围,根据m+n为整数确定m、n的值,从而确定答案.21*cnjy*com
【解答】解:依题意知m>0,﹣ ( http: / / www.21cnjy.com )<0,m﹣n﹣2=0,
故n<0,且n=m﹣2,m+n=m+m﹣2=2m﹣2,
于是0<m<2,
∴﹣2<2m﹣2<2,
又∵m+n为整数,
∴2m﹣2=﹣1,0,1,
故m= ( http: / / www.21cnjy.com ),1, ( http: / / www.21cnjy.com ),
n=﹣ ( http: / / www.21cnjy.com ),﹣1,﹣ ( http: / / www.21cnjy.com ),
∴mn=﹣ ( http: / / www.21cnjy.com )或﹣1.
故选A.
7.(2017 苏州一模)抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且经过点(3,0),则a﹣b+c的值为( )
A.﹣1 B.0 C.1 D.2
【分析】根据二次函数对称性可求出点(3 ( http: / / www.21cnjy.com ),0)关于对称轴直线x=1的对称点为(﹣1,0),然后把(﹣1,0)代入y=ax2+bx+c即可求出答案.
【解答】解:∵抛物线y=ax2+bx+c的对称轴为x=1,
∴根据二次函数的对称性得:点(3,0)的对称点为(﹣1,0),
∵当x=﹣1时,y=a﹣b+c=0,
∴a﹣b+c的值等于0.
故选B.
8.(2017秋 上杭县期中)已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:21cnjy.com
①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.
其中正确的结论的有( )
( http: / / www.21cnjy.com )
A.2个 B.3个 C.4个 D.5个
【分析】根据二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定解答.21·世纪*教育网
【解答】解:开口向下,则a<0,
与y轴交于正半轴,则c>0,
∵﹣ ( http: / / www.21cnjy.com )>0,
∴b>0,
则abc<0,①正确;
∵﹣ ( http: / / www.21cnjy.com )=1,
则b=﹣2a,
∵a﹣b+c<0,
∴3a+c<0,②错误;
∵x=0时,y>0,对称轴是x=1,
∴当x=2时,y>0,
∴4a+2b+c>0,③正确;
∵b=﹣2a,
∴2a+b=0,④正确;
∴b2﹣4ac>0,
∴b2>4ac,⑤正确.
故选:C.
9.(2017 攀枝花)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列命题中正确的是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.a>b>c
B.一次函数y=ax+c的图象不经第四象限
C.m(am+b)+b<a(m是任意实数)
D.3b+2c>0
【分析】由抛物线的开口方向判断a与 ( http: / / www.21cnjy.com )0的关系,由抛物线与y轴的交点得出c的值,然后根据抛物线与x轴交点的个数及x=﹣1时二次函数的值的情况进行推理,进而对所得结论进行判断.
【解答】解:A、由二次函数的图象开口向上可得a>0,由抛物线与y轴交于x轴下方可得c<0,由x=﹣1,得出﹣ ( http: / / www.21cnjy.com )=﹣1,故b>0,b=2a,则b>a>c,故此选项错误;
B、∵a>0,c<0,∴一次函数y=ax+c的图象经一、三、四象限,故此选项错误;
C、当x=﹣1时,y最小,即a﹣b﹣c最小,故a﹣b+c<am2+bm+c,即m(am+b)+b>a,故此选项错误;
D.由图象可知x=1,a+b+c>0,
∵b=2a,
∴a= ( http: / / www.21cnjy.com )b,
∴ ( http: / / www.21cnjy.com )b+b+c>0
∴3b+2c>0,故选项正确;
故选:D.
10.(2017 澧县三模)若抛物线y=x2﹣2x+m的最低点的纵坐标为n,则m﹣n的值是( )
A.﹣1 B.0 C.1 D.2
【分析】依据二次函数求最值的纵坐标公式,可得 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=n,进而有m﹣1=n,于是m﹣n=1.
【解答】解:∵y=x2﹣2x+m,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=n,
即m﹣1=n,
∴m﹣n=1.
故选C.
二.填空题(每小题5分,共30分)
11.(2017 兰州)如图,若抛 ( http: / / www.21cnjy.com )物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为 (﹣2,0) .
( http: / / www.21cnjy.com )
【分析】直接利用二次函数的对称性得出Q点坐标即可.
【解答】解:∵抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,
∴P,Q两点到对称轴x=1的距离相等,
∴Q点的坐标为:(﹣2,0).
故答案为:(﹣2,0).
12.(2017 广陵区校级一模)如果抛物线y=﹣2x2+bx+3的对称轴是x=1,那么b= 4 .
【分析】由抛物线的对称轴是直线x=1,可得出 ( http: / / www.21cnjy.com )=1,解之即可得出b值.
【解答】解:∵抛物线y=﹣2x2+bx+3的对称轴是直线x=1,
∴﹣ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=1,
解得:b=4.
13.(2017 青浦区二模)抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是 直线x=1 .
【分析】直接利用抛物线对称轴公式求出答案.
【解答】解:抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是:直线x=﹣ ( http: / / www.21cnjy.com )=1.
故答案为:直线x=1.
14.(2017 台安县模拟)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ( http: / / www.21cnjy.com ),y2)是抛物线上两点,则y1>y2.其中说法正确的是 ①②④ .
( http: / / www.21cnjy.com )
【分析】根据图象分别求出a、b、c的符号,即 ( http: / / www.21cnjy.com )可判断①;根据对称轴求出b=2a,代入2a﹣b即可判断②;把x=2代入二次函数的解析式,再根据二次函数的性质即可判断③;求出点(﹣5,y1)关于直线x=﹣1的对称点的坐标,根据对称轴判断y1和y2的大小,即可判断④.
【解答】解:①∵二次函数的图象开口向上,
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是直线x=﹣1,
∴﹣ ( http: / / www.21cnjy.com )=﹣1,
∴b=2a>0,
∴abc<0,
故①正确;
②∵b=2a,
∴2a﹣b=0,
故②正确;
③∵抛物线的对称轴为x=﹣1,且过点(﹣3,0),
∴抛物线与x轴另一交点为(1,0).
∵当x>﹣1时,y随x的增大而增大,
∴当x=2时y>0,即4a+2b+c>0,
故③错误;
④∵(﹣5,y1)关于直线x=﹣1的对称点的坐标是(3,y1),
又∵当x>﹣1时,y随x的增大而增大,3> ( http: / / www.21cnjy.com ),
∴y1>y2,
故④正确;
故答案为:①②④.
15.(2017 孝感模拟 ( http: / / www.21cnjy.com ))抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有 ②③④ (填序号).21教育网
( http: / / www.21cnjy.com )
【分析】由抛物线与x轴有两个交点得到b2﹣4ac>0;由抛物线顶点坐标得到抛物线的对称轴为直线x=﹣1,则根据抛物线的对称性得抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,所以当x=1时,y<0,则a+b+c<0;由抛物线的顶点为D(﹣1,2)得a﹣b+c=2,由抛物线的对称轴为直线x=﹣ ( http: / / www.21cnjy.com )=﹣1得b=2a,所以c﹣a=2;根据二次函数的最大值问题,当x=﹣1时,二次函数有最大值为2,即只有x=﹣1时,ax2+bx+c=2,所以说方程ax2+bx+c﹣2=0有两个相等的实数根.
【解答】解:∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,所以①错误;
∵顶点为D(﹣1,2),
∴抛物线的对称轴为直线x=﹣1,
∵抛物线与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,
∴抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,
∴当x=1时,y<0,
∴a+b+c<0,所以②正确;
∵抛物线的顶点为D(﹣1,2),
∴a﹣b+c=2,
∵抛物线的对称轴为直线x=﹣ ( http: / / www.21cnjy.com )=﹣1,
∴b=2a,
∴a﹣2a+c=2,即c﹣a=2,所以③正确;
∵当x=﹣1时,二次函数有最大值为2,
即只有x=﹣1时,ax2+bx+c=2,
∴方程ax2+bx+c﹣2=0有两个相等的实数根,所以④正确.
故答案为②③④.
16.(2015 玄武区 ( http: / / www.21cnjy.com )一模)如图为函数:y=x2﹣1,y=x2+6x+8,y=x2﹣6x+8,y=x2﹣12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2﹣6x+8的图象的序号是 第三个 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
【分析】根据二次函数的对称轴:x=﹣ ( http: / / www.21cnjy.com ),可得答案.
【解答】解:y=x2﹣1对称轴是x=0,图象中第二个,
y=x2+6x+8对称轴是x=﹣3,图象中第一个,
y=x2﹣6x+8对称轴是x=3,图象中第三个,
y=x2﹣12x+35对称轴是x=6,图象中第四个,
故答案为:第三个.①②③④
三.解答题(共20分)
17.(10分)(2017 齐齐哈尔模拟)已知二次函数y=ax2+4x+2的图象经过点A(3,﹣4).21世纪教育网版权所有
(1)求a的值;
(2)求二次函数图象的顶点坐标;
(3)直接写出函数y随x增大而减小的自变量x的取值范围.
【分析】(1)将点A(3,﹣4)代入y=ax2+4x+2,即可求出a的值;
(2)利用配方法将一般式化为顶点式,即可求出此函数图象抛物线的顶点坐标;
(3)根据二次函数的增减性即可求解.
【解答】解:(1)∵二次函数y=ax2+4x+2的图象经过点A(3,﹣4),
∴9a+12+2=﹣4,
∴a=﹣2;
(2)∵y=﹣2x2+4x+2=﹣2(x﹣1)2+4,
∴顶点坐标为(1,4);
(3)∵y=﹣2x2+4x+2中,a=﹣2<0,
抛物线开口向下,对称轴为直线x=1,
∴当x>1时,函数y随自变量增大而减小.
18.(10分)(2017春 邳州市校级月考)在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣3(m>0)与x轴的交点为A,B.【来源:21·世纪·教育·网】
(1)求抛物线的顶点坐标;
(2)若线段AB上有且只有5个点的横坐标为整数,求m的取值范围;
(3)若抛物线在﹣1<x<0位于x轴下方,在3<x<4位于x轴上方,求m的值.
( http: / / www.21cnjy.com )
【分析】(1)利用配方法即可解决问题.
(2)由于抛物线y=mx2﹣2mx+m ( http: / / www.21cnjy.com )﹣3(m>0)的对称轴为直线x=1,线段AB上有且只有5个点的横坐标为整数,于是得到整数为﹣1,0,1,2,3,列不等式组即可得到结论;2-1-c-n-j-y
(3)根据抛物线y=mx2﹣2mx+m ( http: / / www.21cnjy.com )﹣3(m>0)的对称轴为直线x=1,而在3<x<4位于x轴上方,得到抛物线在﹣2<x<﹣1这一段位于x轴的上方,根据已知条件得到抛物线过点(﹣1,0),把(﹣1,0)代入y=mx2﹣2mx+m﹣3即可得到结论.【出处:21教育名师】
【解答】解:(1)∵y=mx2﹣2mx+m﹣3=m(x﹣1)2﹣3,
∴抛物线顶点坐标(1,﹣3);
(2)∵抛物线y=mx2﹣2mx+m﹣3(m>0)的对称轴为直线x=1,
线段AB上有且只有5个点的横坐标为整数,这些整数为﹣1,0,1,2,3,
∴x=2时,y<0;x=4时,y>0;
∴ ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com );
(3)∵抛物线y=mx2﹣2mx+m﹣3(m>0)的对称轴为直线x=1,
而在3<x<4位于x轴上方,
∴抛物线在﹣2<x<﹣1这一段位于x轴的上方,
∵在﹣1<x<0位于x轴下方,
∴抛物线过点(﹣1,0),
把(﹣1,0)代入y=mx2﹣2mx+m﹣3得m+2m+m﹣3=0,
解得m= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
2.2 二次函数的图象与性质
第四课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017 弥勒市二模)已知函数y=ax2+bx+c的图象如图所示,则函数y=ax+b的图象是( )www.21-cn-jy.com
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.(2017 胶州市一模)一次函数y=ax+b(a≠0)与二次函数y=ax2+2x+b(a≠0)在同一直角坐标系中的图象可能是( )www-2-1-cnjy-com
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
3.(2017 宁波)抛物线y=x2﹣2x+m2+2(m是常数)的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2017 陕西)已知抛物线y=x2 ( http: / / www.21cnjy.com )﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )
A.(1,﹣5) B.(3,﹣13) C.(2,﹣8) D.(4,﹣20)
5.(2017 河北区模拟)二次函数y=x2﹣4x﹣4的顶点坐标为( )
A.(2,﹣8) B.(2,8) C.(﹣2,8) D.(﹣2,﹣8)
6.(2017 包头三模)二次函数y=mx2﹣nx﹣2过点(1,0),且函数图象的顶点在第三象限,当m+n为整数时,则mn的值为( )【版权所有:21教育】
A.﹣ ( http: / / www.21cnjy.com ),﹣1 B.﹣ ( http: / / www.21cnjy.com ),﹣2 C.﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),﹣2 D. ( http: / / www.21cnjy.com ),﹣2
7.(2017 苏州一模)抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且经过点(3,0),则a﹣b+c的值为( )21*cnjy*com
A.﹣1 B.0 C.1 D.2
8.(2017秋 上杭县期中)已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.其中正确的结论的有( )
( http: / / www.21cnjy.com )
A.2个 B.3个 C.4个 D.5个
9.(2017 攀枝花)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列命题中正确的是( )
( http: / / www.21cnjy.com )
A.a>b>c
B.一次函数y=ax+c的图象不经第四象限
C.m(am+b)+b<a(m是任意实数)
D.3b+2c>0
10.(2017 澧县三模)若抛物线y=x2﹣2x+m的最低点的纵坐标为n,则m﹣n的值是( )
A.﹣1 B.0 C.1 D.2
二.填空题(每小题5分,共30分)
11.(2017 兰州)如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为 .
( http: / / www.21cnjy.com )
12.(2017 广陵区校级一模)如果抛物线y=﹣2x2+bx+3的对称轴是x=1,那么b= .
13.(2017 青浦区二模)抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是 .
14.(2017 台安县模拟)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ( http: / / www.21cnjy.com ),y2)是抛物线上两点,则y1>y2.其中说法正确的是 .
( http: / / www.21cnjy.com )
15.(2017 孝感模拟)抛物线y=ax ( http: / / www.21cnjy.com )2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有 (填序号).
( http: / / www.21cnjy.com )
16.(2015 玄武区一模)如图为函数: ( http: / / www.21cnjy.com )y=x2﹣1,y=x2+6x+8,y=x2﹣6x+8,y=x2﹣12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2﹣6x+8的图象的序号是 .
( http: / / www.21cnjy.com )
三.解答题(共20分)
17.(10分)(2017 齐齐哈尔模拟)已知二次函数y=ax2+4x+2的图象经过点A(3,﹣4).
(1)求a的值;
(2)求二次函数图象的顶点坐标;
(3)直接写出函数y随x增大而减小的自变量x的取值范围.
18.(10分)(2017春 邳州市校级月考)在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣3(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)若线段AB上有且只有5个点的横坐标为整数,求m的取值范围;
(3)若抛物线在﹣1<x<0位于x轴下方,在3<x<4位于x轴上方,求m的值.
( http: / / www.21cnjy.com )
2.2 二次函数的图象与性质
第四课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 弥勒市二模)已知函数y=ax2+bx+c的图象如图所示,则函数y=ax+b的图象是( )21教育名师原创作品
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】根据抛物线开口向下确定出a<0,再根据对称轴确定出b,然后根据一次函数的性质确定出函数图象即可得解.
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=﹣ ( http: / / www.21cnjy.com )>0,
∴b>0,
∴函数y=ax+b的图象经过第二四象限且与y轴正半轴相交,
故选B.
2.(2017 胶州市一模)一次函数y=ax+b(a≠0)与二次函数y=ax2+2x+b(a≠0)在同一直角坐标系中的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】本题可先由一次函数y=ax+b图象得到字母系数的正负,再与二次函数y=ax2+2x+b的图象相比较看是否一致.
【解答】解:A、由抛物线可知,a>0,得b>0,由直线可知,a<0,b>0,故本选项错误;
B、由抛物线可知,a<0,b>0,由直线可知,a>0,b<0,故本选项错误;
C、由抛物线可知,a<0,b>0,由直线可知,a<0,b<0,故本选项错误;
D、由抛物线可知,a>0,b>0,由直线可知,a>0,b>0,且交y轴同一点,故本选项正确.
故选D.
3.(2017 宁波)抛物线y=x2﹣2x+m2+2(m是常数)的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】先根据抛物线的顶点式求出抛物线y=x2﹣2x+m2+2(m是常数)的顶点坐标,再根据各象限内点的坐标特点进行解答.
【解答】解:∵y=x2﹣2x+m2+2=(x﹣1)2+(m2+1),
∴顶点坐标为:(1,m2+1),
∵1>0,m2+1>0,
∴顶点在第一象限.
故选A.
4.(2017 陕西)已知 ( http: / / www.21cnjy.com )抛物线y=x2﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )
A.(1,﹣5) B.(3,﹣13) C.(2,﹣8) D.(4,﹣20)
【分析】先利用配方法求得点M的坐标,然后利用关于原点对称点的特点得到点M′的坐标,然后将点M′的坐标代入抛物线的解析式求解即可.
【解答】解:y=x2﹣2mx﹣4=x2﹣2mx+m2﹣m2﹣4=(x﹣m)2﹣m2﹣4.
∴点M(m,﹣m2﹣4).
∴点M′(﹣m,m2+4).
∴m2+2m2﹣4=m2+4.
解得m=±2.
∵m>0,
∴m=2.
∴M(2,﹣8).
故选C.
5.(2017 河北区模拟)二次函数y=x2﹣4x﹣4的顶点坐标为( )
A.(2,﹣8) B.(2,8) C.(﹣2,8) D.(﹣2,﹣8)
【分析】把二次函数化成顶点式,可得出二次函数的顶点坐标.
【解答】解:∵y=x2﹣4x﹣4=(x﹣2)2﹣8,
∴其顶点坐标为(2,﹣8),
故选A.
6.(2017 包头三模)二次函数y=mx2﹣nx﹣2过点(1,0),且函数图象的顶点在第三象限,当m+n为整数时,则mn的值为( )21·cn·jy·com
A.﹣ ( http: / / www.21cnjy.com ),﹣1 B.﹣ ( http: / / www.21cnjy.com ),﹣2 C.﹣ ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),﹣2 D. ( http: / / www.21cnjy.com ),﹣2
【分析】首先根据题意确定m、n的符号,然后进一步确定m的取值范围,根据m+n为整数确定m、n的值,从而确定答案.21*cnjy*com
【解答】解:依题意知m>0,﹣ ( http: / / www.21cnjy.com )<0,m﹣n﹣2=0,
故n<0,且n=m﹣2,m+n=m+m﹣2=2m﹣2,
于是0<m<2,
∴﹣2<2m﹣2<2,
又∵m+n为整数,
∴2m﹣2=﹣1,0,1,
故m= ( http: / / www.21cnjy.com ),1, ( http: / / www.21cnjy.com ),
n=﹣ ( http: / / www.21cnjy.com ),﹣1,﹣ ( http: / / www.21cnjy.com ),
∴mn=﹣ ( http: / / www.21cnjy.com )或﹣1.
故选A.
7.(2017 苏州一模)抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且经过点(3,0),则a﹣b+c的值为( )
A.﹣1 B.0 C.1 D.2
【分析】根据二次函数对称性可求出点(3 ( http: / / www.21cnjy.com ),0)关于对称轴直线x=1的对称点为(﹣1,0),然后把(﹣1,0)代入y=ax2+bx+c即可求出答案.
【解答】解:∵抛物线y=ax2+bx+c的对称轴为x=1,
∴根据二次函数的对称性得:点(3,0)的对称点为(﹣1,0),
∵当x=﹣1时,y=a﹣b+c=0,
∴a﹣b+c的值等于0.
故选B.
8.(2017秋 上杭县期中)已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:21cnjy.com
①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.
其中正确的结论的有( )
( http: / / www.21cnjy.com )
A.2个 B.3个 C.4个 D.5个
【分析】根据二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定解答.21·世纪*教育网
【解答】解:开口向下,则a<0,
与y轴交于正半轴,则c>0,
∵﹣ ( http: / / www.21cnjy.com )>0,
∴b>0,
则abc<0,①正确;
∵﹣ ( http: / / www.21cnjy.com )=1,
则b=﹣2a,
∵a﹣b+c<0,
∴3a+c<0,②错误;
∵x=0时,y>0,对称轴是x=1,
∴当x=2时,y>0,
∴4a+2b+c>0,③正确;
∵b=﹣2a,
∴2a+b=0,④正确;
∴b2﹣4ac>0,
∴b2>4ac,⑤正确.
故选:C.
9.(2017 攀枝花)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列命题中正确的是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
A.a>b>c
B.一次函数y=ax+c的图象不经第四象限
C.m(am+b)+b<a(m是任意实数)
D.3b+2c>0
【分析】由抛物线的开口方向判断a与 ( http: / / www.21cnjy.com )0的关系,由抛物线与y轴的交点得出c的值,然后根据抛物线与x轴交点的个数及x=﹣1时二次函数的值的情况进行推理,进而对所得结论进行判断.
【解答】解:A、由二次函数的图象开口向上可得a>0,由抛物线与y轴交于x轴下方可得c<0,由x=﹣1,得出﹣ ( http: / / www.21cnjy.com )=﹣1,故b>0,b=2a,则b>a>c,故此选项错误;
B、∵a>0,c<0,∴一次函数y=ax+c的图象经一、三、四象限,故此选项错误;
C、当x=﹣1时,y最小,即a﹣b﹣c最小,故a﹣b+c<am2+bm+c,即m(am+b)+b>a,故此选项错误;
D.由图象可知x=1,a+b+c>0,
∵b=2a,
∴a= ( http: / / www.21cnjy.com )b,
∴ ( http: / / www.21cnjy.com )b+b+c>0
∴3b+2c>0,故选项正确;
故选:D.
10.(2017 澧县三模)若抛物线y=x2﹣2x+m的最低点的纵坐标为n,则m﹣n的值是( )
A.﹣1 B.0 C.1 D.2
【分析】依据二次函数求最值的纵坐标公式,可得 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=n,进而有m﹣1=n,于是m﹣n=1.
【解答】解:∵y=x2﹣2x+m,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=n,
即m﹣1=n,
∴m﹣n=1.
故选C.
二.填空题(每小题5分,共30分)
11.(2017 兰州)如图,若抛 ( http: / / www.21cnjy.com )物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为 (﹣2,0) .
( http: / / www.21cnjy.com )
【分析】直接利用二次函数的对称性得出Q点坐标即可.
【解答】解:∵抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,
∴P,Q两点到对称轴x=1的距离相等,
∴Q点的坐标为:(﹣2,0).
故答案为:(﹣2,0).
12.(2017 广陵区校级一模)如果抛物线y=﹣2x2+bx+3的对称轴是x=1,那么b= 4 .
【分析】由抛物线的对称轴是直线x=1,可得出 ( http: / / www.21cnjy.com )=1,解之即可得出b值.
【解答】解:∵抛物线y=﹣2x2+bx+3的对称轴是直线x=1,
∴﹣ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=1,
解得:b=4.
13.(2017 青浦区二模)抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是 直线x=1 .
【分析】直接利用抛物线对称轴公式求出答案.
【解答】解:抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是:直线x=﹣ ( http: / / www.21cnjy.com )=1.
故答案为:直线x=1.
14.(2017 台安县模拟)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ( http: / / www.21cnjy.com ),y2)是抛物线上两点,则y1>y2.其中说法正确的是 ①②④ .
( http: / / www.21cnjy.com )
【分析】根据图象分别求出a、b、c的符号,即 ( http: / / www.21cnjy.com )可判断①;根据对称轴求出b=2a,代入2a﹣b即可判断②;把x=2代入二次函数的解析式,再根据二次函数的性质即可判断③;求出点(﹣5,y1)关于直线x=﹣1的对称点的坐标,根据对称轴判断y1和y2的大小,即可判断④.
【解答】解:①∵二次函数的图象开口向上,
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是直线x=﹣1,
∴﹣ ( http: / / www.21cnjy.com )=﹣1,
∴b=2a>0,
∴abc<0,
故①正确;
②∵b=2a,
∴2a﹣b=0,
故②正确;
③∵抛物线的对称轴为x=﹣1,且过点(﹣3,0),
∴抛物线与x轴另一交点为(1,0).
∵当x>﹣1时,y随x的增大而增大,
∴当x=2时y>0,即4a+2b+c>0,
故③错误;
④∵(﹣5,y1)关于直线x=﹣1的对称点的坐标是(3,y1),
又∵当x>﹣1时,y随x的增大而增大,3> ( http: / / www.21cnjy.com ),
∴y1>y2,
故④正确;
故答案为:①②④.
15.(2017 孝感模拟 ( http: / / www.21cnjy.com ))抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有 ②③④ (填序号).21教育网
( http: / / www.21cnjy.com )
【分析】由抛物线与x轴有两个交点得到b2﹣4ac>0;由抛物线顶点坐标得到抛物线的对称轴为直线x=﹣1,则根据抛物线的对称性得抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,所以当x=1时,y<0,则a+b+c<0;由抛物线的顶点为D(﹣1,2)得a﹣b+c=2,由抛物线的对称轴为直线x=﹣ ( http: / / www.21cnjy.com )=﹣1得b=2a,所以c﹣a=2;根据二次函数的最大值问题,当x=﹣1时,二次函数有最大值为2,即只有x=﹣1时,ax2+bx+c=2,所以说方程ax2+bx+c﹣2=0有两个相等的实数根.
【解答】解:∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,所以①错误;
∵顶点为D(﹣1,2),
∴抛物线的对称轴为直线x=﹣1,
∵抛物线与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,
∴抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,
∴当x=1时,y<0,
∴a+b+c<0,所以②正确;
∵抛物线的顶点为D(﹣1,2),
∴a﹣b+c=2,
∵抛物线的对称轴为直线x=﹣ ( http: / / www.21cnjy.com )=﹣1,
∴b=2a,
∴a﹣2a+c=2,即c﹣a=2,所以③正确;
∵当x=﹣1时,二次函数有最大值为2,
即只有x=﹣1时,ax2+bx+c=2,
∴方程ax2+bx+c﹣2=0有两个相等的实数根,所以④正确.
故答案为②③④.
16.(2015 玄武区 ( http: / / www.21cnjy.com )一模)如图为函数:y=x2﹣1,y=x2+6x+8,y=x2﹣6x+8,y=x2﹣12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2﹣6x+8的图象的序号是 第三个 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
【分析】根据二次函数的对称轴:x=﹣ ( http: / / www.21cnjy.com ),可得答案.
【解答】解:y=x2﹣1对称轴是x=0,图象中第二个,
y=x2+6x+8对称轴是x=﹣3,图象中第一个,
y=x2﹣6x+8对称轴是x=3,图象中第三个,
y=x2﹣12x+35对称轴是x=6,图象中第四个,
故答案为:第三个.①②③④
三.解答题(共20分)
17.(10分)(2017 齐齐哈尔模拟)已知二次函数y=ax2+4x+2的图象经过点A(3,﹣4).21世纪教育网版权所有
(1)求a的值;
(2)求二次函数图象的顶点坐标;
(3)直接写出函数y随x增大而减小的自变量x的取值范围.
【分析】(1)将点A(3,﹣4)代入y=ax2+4x+2,即可求出a的值;
(2)利用配方法将一般式化为顶点式,即可求出此函数图象抛物线的顶点坐标;
(3)根据二次函数的增减性即可求解.
【解答】解:(1)∵二次函数y=ax2+4x+2的图象经过点A(3,﹣4),
∴9a+12+2=﹣4,
∴a=﹣2;
(2)∵y=﹣2x2+4x+2=﹣2(x﹣1)2+4,
∴顶点坐标为(1,4);
(3)∵y=﹣2x2+4x+2中,a=﹣2<0,
抛物线开口向下,对称轴为直线x=1,
∴当x>1时,函数y随自变量增大而减小.
18.(10分)(2017春 邳州市校级月考)在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣3(m>0)与x轴的交点为A,B.【来源:21·世纪·教育·网】
(1)求抛物线的顶点坐标;
(2)若线段AB上有且只有5个点的横坐标为整数,求m的取值范围;
(3)若抛物线在﹣1<x<0位于x轴下方,在3<x<4位于x轴上方,求m的值.
( http: / / www.21cnjy.com )
【分析】(1)利用配方法即可解决问题.
(2)由于抛物线y=mx2﹣2mx+m ( http: / / www.21cnjy.com )﹣3(m>0)的对称轴为直线x=1,线段AB上有且只有5个点的横坐标为整数,于是得到整数为﹣1,0,1,2,3,列不等式组即可得到结论;2-1-c-n-j-y
(3)根据抛物线y=mx2﹣2mx+m ( http: / / www.21cnjy.com )﹣3(m>0)的对称轴为直线x=1,而在3<x<4位于x轴上方,得到抛物线在﹣2<x<﹣1这一段位于x轴的上方,根据已知条件得到抛物线过点(﹣1,0),把(﹣1,0)代入y=mx2﹣2mx+m﹣3即可得到结论.【出处:21教育名师】
【解答】解:(1)∵y=mx2﹣2mx+m﹣3=m(x﹣1)2﹣3,
∴抛物线顶点坐标(1,﹣3);
(2)∵抛物线y=mx2﹣2mx+m﹣3(m>0)的对称轴为直线x=1,
线段AB上有且只有5个点的横坐标为整数,这些整数为﹣1,0,1,2,3,
∴x=2时,y<0;x=4时,y>0;
∴ ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com );
(3)∵抛物线y=mx2﹣2mx+m﹣3(m>0)的对称轴为直线x=1,
而在3<x<4位于x轴上方,
∴抛物线在﹣2<x<﹣1这一段位于x轴的上方,
∵在﹣1<x<0位于x轴下方,
∴抛物线过点(﹣1,0),
把(﹣1,0)代入y=mx2﹣2mx+m﹣3得m+2m+m﹣3=0,
解得m= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
