青岛版初一数学10.3平行线的性质 课件
文档属性
| 名称 | 青岛版初一数学10.3平行线的性质 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 230.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-23 00:00:00 | ||
图片预览



文档简介
课件16张PPT。§10.3 平行线的性质学习目标:
1.探索直线平行性质的推导过程,掌握平行
线的三条性质 。
2.能运用三条性质进行简单的推理和计算。
重点:平行线的三个性质。
难点:平行线三个性质的应用。
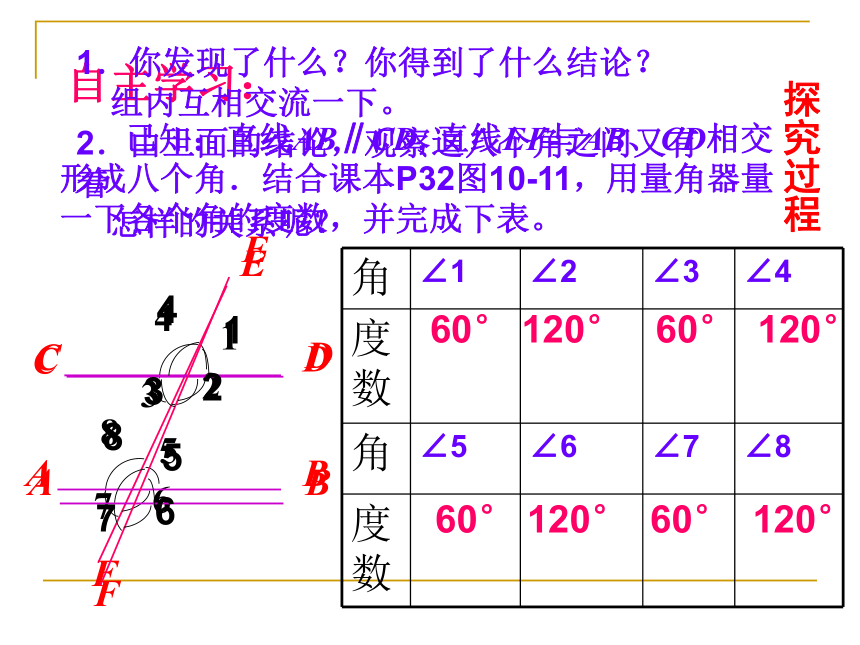
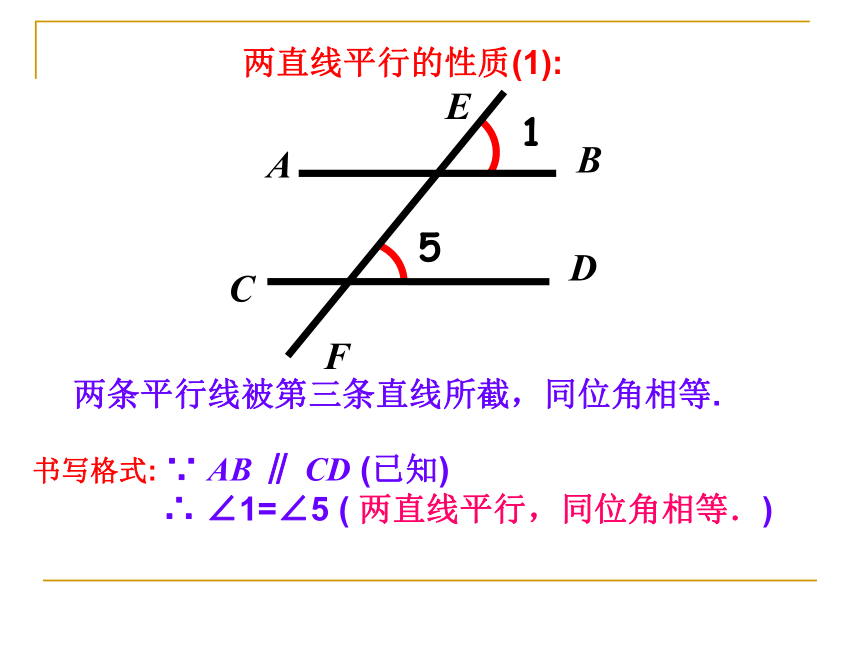
60° 120° 60° 120° 60° 120° 60° 120° 探究过程两直线平行的性质(1):两条平行线被第三条直线所截,同位角相等.
书写格式: ∵ AB ∥ CD (已知)
∴ ∠1=∠5 ( 两直线平行,同位角相等.)
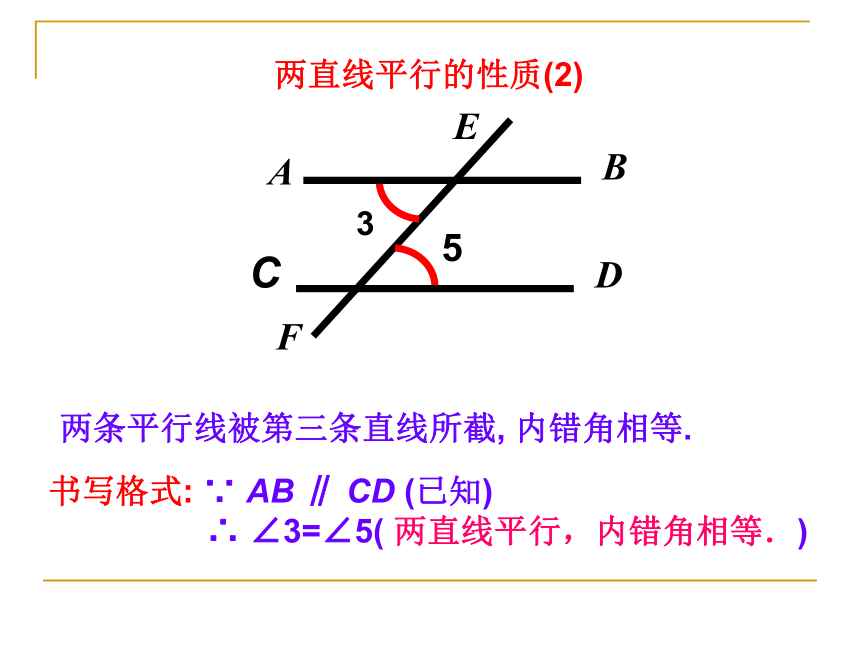
两直线平行的性质(2)两条平行线被第三条直线所截, 内错角相等.
书写格式: ∵ AB ∥ CD (已知)
∴ ∠3=∠5( 两直线平行,内错角相等.)
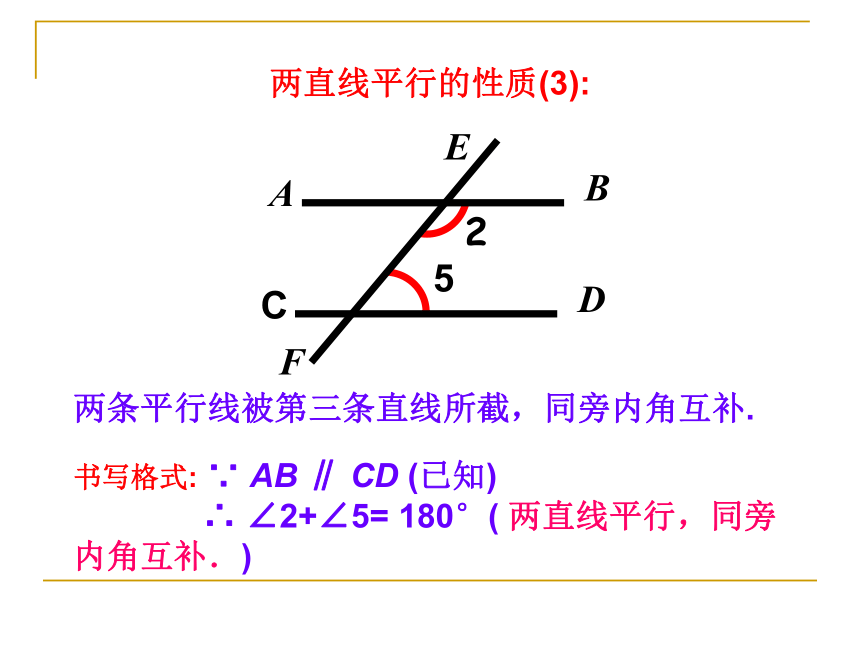
C两直线平行的性质(3):5F2两条平行线被第三条直线所截,同旁内角互补.
书写格式: ∵ AB ∥ CD (已知)
∴ ∠2+∠5= 180°( 两直线平行,同旁 内角互补.)
如图,已知平行线AB,CD被直线AE所截.填空:⑴ ∵AB∥CD,∴∠2 =____ =____(两直线平行, ____角相等)⑵ ∵ AB∥CD ,∴∠3=____=____(两直线平行, ____角相等) ⑶ ∵AB∥CD,∴∠1+∠4=____(两直线平行,
同旁内角____)
∴ ∠4=____________ =____________=________∠1110°内错∠1110°同位180°互补180°—∠1180°—110°70°练一练平行线有哪些性质? 1、如果两直线平行,那么同位角相等. 2、如果两直线平行,那么内错角相等.
3、如果两直线平行,那么同旁内角互补.总结 如右图,直线a ∥ b,c ∥ d, ∠1= 106 ° 求∠ 2、∠3的度数。解: ∵ a ∥ b, ∵ c ∥ d,例1∴ ∠ 1=∠2, (两直线平行,内错角相等).
又∵∠ 1=106 ° ,
∴ ∠ 2=106 °.
∴ ∠ 2=∠3, (两直线平行,同位角相等).
又∵ ∠ 2=106 °,
∴∠ 3=106 °.如图.AB∥DE, DF∥BC , ∠1= 62 °,求 ∠2、∠3的 度数.(用数学语言表述求解过程)跟踪训练跟踪训练如图.AB∥DE, DF∥BC , ∠1= 62 °,求 ∠2、∠3的 度数.(用数学语言表述求解过程)例1、解: ∵ a ∥ b, ∴ ∠ 1=∠2,(两直线平行,内错角相等).
又∵∠ 1=106 ° , ∴ ∠ 2=106 °.
∵ c ∥ d,∴ ∠ 2=∠3, (两直线平行,同位角相等).
又∵ ∠ 2=106 °,∴∠ 3=106 °.
解: ∵ DF∥BC ,
∴ ∠1+ ∠2= 180 °,(两直线平行,同旁内角互补)
又∵ ∠1= 62 °,
∴∠2= 180 °—∠1 = 180 °— 62 °= 118 °.
跟踪训练 ∵ AB∥DE,
∴ ∠ 3 =∠ 2 = 118 °(两直线平行,同位角相等).
如图.AB∥DE, DF∥BC , ∠1= 62 °,求 ∠2、∠3的 度数.(用数学语言表述求解 过程)如图梯子的各条横档互相平行, ∠1=100 °,求∠2 的度数。解: ∵ CD∥AB
∴∠ 3 = ∠ 1 = 100 °
(两直线平行,同位角相等) 又∵ ∠2+ ∠3 =180°
∴ ∠2 = 180° —∠3
= 180°—100°= 80°.拓展提升随堂检测1.如图1,直线a与直线b被直线c所截,
a ∥ b, ∠1= 62 ° ,则∠3=________
2.如图2所示,已知AB∥CD,∠1= 80 °,
则∠2=________
3.∠1和∠2是直线AB、CD被直线EF
所截而成的内错角,那么∠1和∠2 的大小关系是( )
A.∠1=∠2 B.∠1>∠2;
C.∠1<∠2 D.无法确定
4、如图3, AB∥DE, ∠B= 50 °,求 ∠1、 ∠2 、∠3的度数. 随堂检测1.如图1,直线a与直线b被直线c所截,
a ∥ b, ∠1= 62 ° ,则∠3=________
2.如图2所示,已知AB∥CD,∠1= 80 °,
则∠2=________
3.∠1和∠2是直线AB、CD被直线EF
所截而成的内错角,那么∠1和∠2 的大小关系是( )
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
D62°100 °作业:
A组:课本练习第2题,习题A的1、2题.
B组:课本习题A第3题,B组的1题.
1.探索直线平行性质的推导过程,掌握平行
线的三条性质 。
2.能运用三条性质进行简单的推理和计算。
重点:平行线的三个性质。
难点:平行线三个性质的应用。
60° 120° 60° 120° 60° 120° 60° 120° 探究过程两直线平行的性质(1):两条平行线被第三条直线所截,同位角相等.
书写格式: ∵ AB ∥ CD (已知)
∴ ∠1=∠5 ( 两直线平行,同位角相等.)
两直线平行的性质(2)两条平行线被第三条直线所截, 内错角相等.
书写格式: ∵ AB ∥ CD (已知)
∴ ∠3=∠5( 两直线平行,内错角相等.)
C两直线平行的性质(3):5F2两条平行线被第三条直线所截,同旁内角互补.
书写格式: ∵ AB ∥ CD (已知)
∴ ∠2+∠5= 180°( 两直线平行,同旁 内角互补.)
如图,已知平行线AB,CD被直线AE所截.填空:⑴ ∵AB∥CD,∴∠2 =____ =____(两直线平行, ____角相等)⑵ ∵ AB∥CD ,∴∠3=____=____(两直线平行, ____角相等) ⑶ ∵AB∥CD,∴∠1+∠4=____(两直线平行,
同旁内角____)
∴ ∠4=____________ =____________=________∠1110°内错∠1110°同位180°互补180°—∠1180°—110°70°练一练平行线有哪些性质? 1、如果两直线平行,那么同位角相等. 2、如果两直线平行,那么内错角相等.
3、如果两直线平行,那么同旁内角互补.总结 如右图,直线a ∥ b,c ∥ d, ∠1= 106 ° 求∠ 2、∠3的度数。解: ∵ a ∥ b, ∵ c ∥ d,例1∴ ∠ 1=∠2, (两直线平行,内错角相等).
又∵∠ 1=106 ° ,
∴ ∠ 2=106 °.
∴ ∠ 2=∠3, (两直线平行,同位角相等).
又∵ ∠ 2=106 °,
∴∠ 3=106 °.如图.AB∥DE, DF∥BC , ∠1= 62 °,求 ∠2、∠3的 度数.(用数学语言表述求解过程)跟踪训练跟踪训练如图.AB∥DE, DF∥BC , ∠1= 62 °,求 ∠2、∠3的 度数.(用数学语言表述求解过程)例1、解: ∵ a ∥ b, ∴ ∠ 1=∠2,(两直线平行,内错角相等).
又∵∠ 1=106 ° , ∴ ∠ 2=106 °.
∵ c ∥ d,∴ ∠ 2=∠3, (两直线平行,同位角相等).
又∵ ∠ 2=106 °,∴∠ 3=106 °.
解: ∵ DF∥BC ,
∴ ∠1+ ∠2= 180 °,(两直线平行,同旁内角互补)
又∵ ∠1= 62 °,
∴∠2= 180 °—∠1 = 180 °— 62 °= 118 °.
跟踪训练 ∵ AB∥DE,
∴ ∠ 3 =∠ 2 = 118 °(两直线平行,同位角相等).
如图.AB∥DE, DF∥BC , ∠1= 62 °,求 ∠2、∠3的 度数.(用数学语言表述求解 过程)如图梯子的各条横档互相平行, ∠1=100 °,求∠2 的度数。解: ∵ CD∥AB
∴∠ 3 = ∠ 1 = 100 °
(两直线平行,同位角相等) 又∵ ∠2+ ∠3 =180°
∴ ∠2 = 180° —∠3
= 180°—100°= 80°.拓展提升随堂检测1.如图1,直线a与直线b被直线c所截,
a ∥ b, ∠1= 62 ° ,则∠3=________
2.如图2所示,已知AB∥CD,∠1= 80 °,
则∠2=________
3.∠1和∠2是直线AB、CD被直线EF
所截而成的内错角,那么∠1和∠2 的大小关系是( )
A.∠1=∠2 B.∠1>∠2;
C.∠1<∠2 D.无法确定
4、如图3, AB∥DE, ∠B= 50 °,求 ∠1、 ∠2 、∠3的度数. 随堂检测1.如图1,直线a与直线b被直线c所截,
a ∥ b, ∠1= 62 ° ,则∠3=________
2.如图2所示,已知AB∥CD,∠1= 80 °,
则∠2=________
3.∠1和∠2是直线AB、CD被直线EF
所截而成的内错角,那么∠1和∠2 的大小关系是( )
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
D62°100 °作业:
A组:课本练习第2题,习题A的1、2题.
B组:课本习题A第3题,B组的1题.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
