2.4 二次函数的应用(2)一课一测
文档属性
| 名称 | 2.4 二次函数的应用(2)一课一测 |  | |
| 格式 | doc | ||
| 文件大小 | 454.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-24 21:39:39 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
2.4 二次函数的应用
第二课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017 繁昌县模拟)某企业是一家 ( http: / / www.21cnjy.com )专门生产季节性产品的企业,当产品无利润时,企业会自动停产,经过调研预测,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=﹣n2+14n﹣24,则企业停产的月份为( )
A.2月和12月 B.2月至12月 C.1月 D.1月、2月和12月
2.(2017 岱岳区模拟)山东全省201 ( http: / / www.21cnjy.com )6年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )21·世纪*教育网
A.140元 B.150元 C.160元 D.180元
3.(2017 蒙阴县一模)某商人将单价为 ( http: / / www.21cnjy.com )8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高( )21教育名师原创作品
A.8元或10元 B.12元 C.8元 D.10元
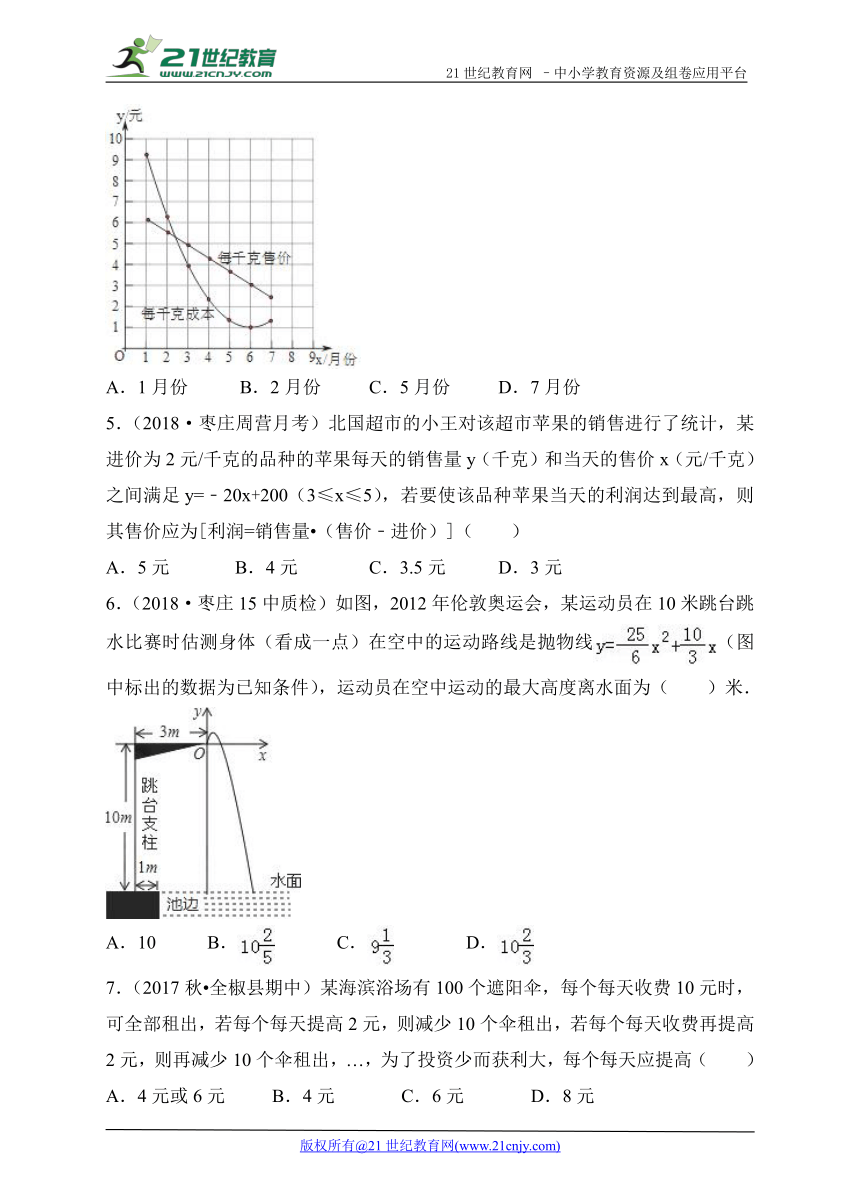
4.(2018·滕州鲍沟月 ( http: / / www.21cnjy.com )考)在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )21*cnjy*com
( http: / / www.21cnjy.com )
A.1月份 B.2月份 C.5月份 D.7月份
5.(2018·枣庄周营月考)北国超市 ( http: / / www.21cnjy.com )的小王对该超市苹果的销售进行了统计,某进价为2元/千克的品种的苹果每天的销售量y(千克)和当天的售价x(元/千克)之间满足y=﹣20x+200(3≤x≤5),若要使该品种苹果当天的利润达到最高,则其售价应为[利润=销售量 (售价﹣进价)]( )21*cnjy*com
A.5元 B.4元 C.3.5元 D.3元
6.(2018·枣庄15中质检)如图,2012年伦敦奥运会,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线 ( http: / / www.21cnjy.com )(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为( )米.
( http: / / www.21cnjy.com )
A.10 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
7.(2017秋 全椒县期中)某海 ( http: / / www.21cnjy.com )滨浴场有100个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,…,为了投资少而获利大,每个每天应提高( )
A.4元或6元 B.4元 C.6元 D.8元
8.(2017春 正定县期中)下表 ( http: / / www.21cnjy.com )所列为某商店薄利多销的情况,某商品原价为560元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为500元时,日销量为( )件.
降价(元) 5 10 15 20 25 30 35
日销量(件) 780 810 840 870 900 930 960
A.1200 B.750 C.1110 D.1140
9.(2017春 鼓楼区校级月考)市场调查表明:某种一周内水果的销售率y(销售率= ( http: / / www.21cnjy.com ))与价格倍数x(价格倍数= ( http: / / www.21cnjy.com ))的关系满足函数关系y=﹣ ( http: / / www.21cnjy.com )x+ ( http: / / www.21cnjy.com )(1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
A.120% B.80% C.60% D.40%
10.(2018 枣庄实验质检)一件工艺品的 ( http: / / www.21cnjy.com )进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )
A.3.6 元 B.5 元 C.10 元 D.12 元
二.填空题(每小题5分,共30分)
11.(2017 沈阳)某 ( http: / / www.21cnjy.com )商场购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可销售出400件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,当销售量单价是 元/件,才能在半月内获得最大利润.www-2-1-cnjy-com
12.(2017秋 乳山 ( http: / / www.21cnjy.com )市期中)某商店经销一种成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克,若销售价每涨1元,则月销售量减少10千克.要使月销售利润达到最大,销售单价应定为 元.
13.(2018 滕州月考)某电商销售 ( http: / / www.21cnjy.com )一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 .
14.(2018 烟台质检)竖直上抛的 ( http: / / www.21cnjy.com )小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
15.(2018 泰安质检)某大学生利用业余时间销售一种进价为60元/件的文化衫,前期了解并整理了销售这种文化衫的相关信息如下:
(1)月销量y(件)与售价x(元)的关系满足:y=﹣2x+400;
(2)工商部门限制销售价x满足:70≤x≤150(计算月利润时不考虑其他成本).给出下列结论:
①这种文化衫的月销量最小为100件;
②这种文化衫的月销量最大为260件;
③销售这种文化衫的月利润最小为2600元;
④销售这种文化衫的月利润最大为9000元.
其中正确的是 (把所有正确结论的序号都选上)
16.(2018 台儿庄月考)某超 ( http: / / www.21cnjy.com )市销售某种玩具,进货价为20元.根据市场调查:在一段时间内,销售单价是30元时,销售量是400件,而销售单价每上涨1元,就会少售出10件玩具,超市要完成不少于300件的销售任务,又要获得最大利润,则销售单价应定为 元.
三.解答题(共20分)
17.(10分)(2017秋 上杭县期中 ( http: / / www.21cnjy.com ))“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,商场决定采取适当的降价措施.经调查发现,每件该商品每降价1元,商场平均每天可多售出10件.设每件商品降价x元,请回答:
(1)降价后每件商品盈利 元,商场日销售量 件(用含x的代数式表示);
(2)求每件商品降价多少元时,商场日盈利可达到最大?最大日盈利是多少元?
18.(10分)(2017 济宁)某 ( http: / / www.21cnjy.com )商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=﹣x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
2.4 二次函数的应用
第二课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 繁昌县模拟)某企业是一 ( http: / / www.21cnjy.com )家专门生产季节性产品的企业,当产品无利润时,企业会自动停产,经过调研预测,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=﹣n2+14n﹣24,则企业停产的月份为( )
A.2月和12月 B.2月至12月
C.1月 D.1月、2月和12月
【分析】知道利润y和月份n之间函数关系式,求利润y大于0时x的取值.
【解答】解:由题意知,
利润y和月份n之间函数关系式为y=﹣n2+14n﹣24,
∴y=﹣(n﹣2)(n﹣12),
当n=1时,y<0,
当n=2时,y=0,
当n=12时,y=0,
故停产的月份是1月、2月、12月.
故选D.
2.(2017 岱岳区模拟)山 ( http: / / www.21cnjy.com )东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )21教育网
A.140元 B.150元 C.160元 D.180元
【分析】设每张床位提高x个单位,每天收 ( http: / / www.21cnjy.com )入为y元,根据等量关系“每天收入=每张床的费用×每天出租的床位”可求出y与x之间的函数关系式,运用公式求最值即可.
【解答】解:设每张床位提高x个20元,每天收入为y元.
则有y=(100+20x)(100﹣10x)
=﹣200x2+1000x+10000.
当x=﹣ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=2.5时,可使y有最大值.
又x为整数,则x=2时,y=11200;
x=3时,y=11200;
则为使租出的床位少且租金高,每张床收费=100+3×20=160元,
故选:C.
3.(2017 蒙阴县一模)某商人将单价为 ( http: / / www.21cnjy.com )8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高( )
A.8元或10元 B.12元 C.8元 D.10元
【分析】每件利润为(x﹣8)元,销售量为(100﹣10× ( http: / / www.21cnjy.com )),根据利润=每件利润×销售量,得出销售利润y(元)与售单价x(元)之间的函数关系;再根据函数关系式,利用二次函数的性质求最大利润.
【解答】解:(1)依题意,得y=(x﹣8) (100﹣10× ( http: / / www.21cnjy.com ))=﹣x2+190x﹣1200
=﹣5(x﹣19)2+605,﹣5<0,
∴抛物线开口向下,函数有最大值,
即当x=19时,y的最大值为605,
∵售价为偶数,
∴x为18或20,
当x=18时,y=600,
当x=20时,y=600,
∴x为18或20时y的值相同,
∴商品提高了18﹣10=8(元)或20﹣10=10(元)
故选A.
4.(2018·滕州鲍沟月考 ( http: / / www.21cnjy.com ))在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )21世纪教育网版权所有
( http: / / www.21cnjy.com )
A.1月份 B.2月份 C.5月份 D.7月份
【分析】先根据图中的信息用待定系数法表 ( http: / / www.21cnjy.com )示出每千克售价的一次函数以及每千克成本的二次函数,然后每千克收益=每千克售价﹣每千克成本,得出关于收益和月份的函数关系式,根据函数的性质得出收益的最值以及相应的月份.
【解答】解:设x月份出售时,每千克售价为y1元,每千克成本为y2元.
根据图甲设y1=kx+b,
∴ ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com ),
∴y1=﹣ ( http: / / www.21cnjy.com )x+7.
根据图乙设y2=a(x﹣6)2+1,
∴4=a(3﹣6)2+1,
∴a= ( http: / / www.21cnjy.com ),
∴y2= ( http: / / www.21cnjy.com )(x﹣6)2+1.
∵y=y1﹣y2,
∴y=﹣ ( http: / / www.21cnjy.com )x+7﹣[ ( http: / / www.21cnjy.com )(x﹣6)2+1],
∴y=﹣ ( http: / / www.21cnjy.com )x2+ ( http: / / www.21cnjy.com )x﹣6.
∵y=﹣ ( http: / / www.21cnjy.com )x2+ ( http: / / www.21cnjy.com )x﹣6,
∴y=﹣ ( http: / / www.21cnjy.com )(x﹣5)2+ ( http: / / www.21cnjy.com ).
∴当x=5时,y有最大值,即当5月份出售时,每千克收益最大.
故选C.
5.(2018·枣庄周营月考)北国超市 ( http: / / www.21cnjy.com )的小王对该超市苹果的销售进行了统计,某进价为2元/千克的品种的苹果每天的销售量y(千克)和当天的售价x(元/千克)之间满足y=﹣20x+200(3≤x≤5),若要使该品种苹果当天的利润达到最高,则其售价应为[利润=销售量 (售价﹣进价)]( )2·1·c·n·j·y
A.5元 B.4元 C.3.5元 D.3元
【分析】设销售这种苹果所获得的利润为w, ( http: / / www.21cnjy.com )根据“利润=销售量 (售价﹣进价)“列出函数解析式,并配方成顶点式,利用二次函数的性质可得其最值情况.
【解答】解:设销售这种苹果所获得的利润为w,
则w=(x﹣2)(﹣20x+200)
=﹣20x2+240x﹣400
=﹣20(x﹣6)2+320,
∴当x<6时,w随x的增大而增大,
∵3≤x≤5,
∴当x=5时,w取得最大值,即该品种苹果当天的利润达到最高,
故选:A.
6.(2018·枣庄15中质检)如图,2012年伦敦奥运会,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线 ( http: / / www.21cnjy.com )(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为( )米.
( http: / / www.21cnjy.com )
A.10 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】首先把抛物线解析式配成顶点式,从而得到抛物线的顶点坐标,进而得到运动员在空中运动的最大高度离水面为多少米.2-1-c-n-j-y
【解答】解:∵ ( http: / / www.21cnjy.com )=﹣ ( http: / / www.21cnjy.com )(x2﹣ ( http: / / www.21cnjy.com )x)=﹣ ( http: / / www.21cnjy.com )(x﹣ ( http: / / www.21cnjy.com ))2+ ( http: / / www.21cnjy.com ),
∴抛物线的顶点坐标是( ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )),
∴运动员在空中运动的最大高度离水面为:10+ ( http: / / www.21cnjy.com )=10 ( http: / / www.21cnjy.com )(米),
故选:D.
7.(2017秋 全椒县期中)某海滨浴场有1 ( http: / / www.21cnjy.com )00个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,…,为了投资少而获利大,每个每天应提高( )
A.4元或6元 B.4元 C.6元 D.8元
【分析】设每个遮阳伞每天应提高x元,每天获得利润为S,每个每天应收费(10+x)元,每天的租出量为(100﹣ ( http: / / www.21cnjy.com )×10=100﹣5x)个,由此列出函数解析式即可解答.
【解答】解:设每个遮阳伞每天应提高x元,每天获得利润为S,由此可得,
S=(10+x)(100﹣ ( http: / / www.21cnjy.com )×10),
整理得S=﹣5x2+50x+1000,
=﹣5(x﹣5)2+1125,
因为每天提高2元,则减少10个,所以当提高4元或6元的时候,获利最大,
又因为为了投资少而获利大,因此应提高6元;
故选C.
8.(2017春 正定县期中)下表所 ( http: / / www.21cnjy.com )列为某商店薄利多销的情况,某商品原价为560元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为500元时,日销量为( )件.【来源:21cnj*y.co*m】
降价(元) 5 10 15 20 25 30 35
日销量(件) 780 810 840 870 900 930 960
A.1200 B.750 C.1110 D.1140
【分析】由表中数据得,每降5元,销售量增加30件,则降60元时,销售量为780加上(60﹣5)×6.【版权所有:21教育】
【解答】解:由表中数据得,每降5元,销售量增加30件,
即每降1元,销售量增加6件,
降560﹣500=60元时,销售量为780+(60﹣5)×6=1110(件).
故选C.
9.(2017春 鼓楼区校级月考)市场调查表明:某种一周内水果的销售率y(销售率= ( http: / / www.21cnjy.com ))与价格倍数x(价格倍数= ( http: / / www.21cnjy.com ))的关系满足函数关系y=﹣ ( http: / / www.21cnjy.com )x+ ( http: / / www.21cnjy.com )(1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
A.120% B.80% C.60% D.40%
【分析】设这种水果的进货价格为a,则售出价格为ax,进货数量为b,则售出数量为by,利润率为p,根据“利润率= ( http: / / www.21cnjy.com )”列出p关于x的函数解析式,利用二次函数的性质求得最值即可.
【解答】解:设这种水果的进货价格为a,则售出价格为ax,进货数量为b,则售出数量为by,利润率为p,
则p= ( http: / / www.21cnjy.com )
=y(x﹣1)
=(﹣ ( http: / / www.21cnjy.com )x+ ( http: / / www.21cnjy.com ))(x﹣1)
=﹣ ( http: / / www.21cnjy.com )x2+ ( http: / / www.21cnjy.com )x﹣ ( http: / / www.21cnjy.com )
=﹣ ( http: / / www.21cnjy.com )(x﹣ ( http: / / www.21cnjy.com ))2+ ( http: / / www.21cnjy.com ),
∵商品售价不得超过进货价格的2倍,
∴x≤2,
∵当x< ( http: / / www.21cnjy.com )时,利润率p随x的增大而减小,
∴当x=2时,p取得最大值,最大值为0.8=80%,
故选:B.
10.(2018 枣庄实验质检)一件工 ( http: / / www.21cnjy.com )艺品的进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )21·cn·jy·com
A.3.6 元 B.5 元 C.10 元 D.12 元
【分析】设每件降价x元,每天获得的利润记 ( http: / / www.21cnjy.com )为W,依据:每天获得的总利润=每件工艺品的利润×每天的销售量,列出函数关系式,配方成顶点式即可得其最值情况.
【解答】解:设每件降价x元,每天获得的利润记为W,
根据题意,W=(135﹣x﹣100)(100+4x)
=﹣4x2+40x+3500
=﹣4(x﹣5)2+3600,
∵﹣4<0,
∴当x=5时,W取得最大值,最大值为3600,
即每件降价5元时,每天获得的利润最大,最大利润为3600元.
故选:B.
二.填空题(每小题5分,共30分)
11.(2017 沈阳)某商场购进 ( http: / / www.21cnjy.com )一批单价为20元的日用商品,如果以单价30元销售,那么半月内可销售出400件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,当销售量单价是 35 元/件,才能在半月内获得最大利润.
【分析】设销售单价为x元,销售利润为y元,求得函数关系式,利用二次函数的性质即可解决问题.
【解答】解:设销售单价为x元,销售利润为y元.
根据题意,得:
y=(x﹣20)[400﹣20(x﹣30)]
=(x﹣20)(1000﹣20x)
=﹣20x2+1400x﹣20000
=﹣20(x﹣35)2+4500,
∵﹣20<0,
∴x=35时,y有最大值,
故答案为35.
12.(2017秋 乳山市期中)某商 ( http: / / www.21cnjy.com )店经销一种成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克,若销售价每涨1元,则月销售量减少10千克.要使月销售利润达到最大,销售单价应定为 70 元.
【分析】设销售单价定为每千克x元,获得 ( http: / / www.21cnjy.com )利润为w元,则可以根据成本,求出每千克的利润,以及按照销售价每涨1元,月销售量就减少10千克,可求出销量.从而得到总利润关系式.
【解答】解:设销售单价定为每千克x元,获得利润为w元,则:
w=(x﹣40)[500﹣(x﹣50)×10],
=(x﹣40)(1000﹣10x),
=﹣10x2+1400x﹣40000,
=﹣10(x﹣70)2+9000,
故当x=70时,利润最大为9000元.
答:要使月销售利润达到最大,销售单价应定为70元.
故答案为70.
13.(2018 滕州月考) ( http: / / www.21cnjy.com )某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 0<a<6 .
【分析】根据题意可以列出相应的不等式,从而可以解答本题.
【解答】解:设未来30天每天获得的利润为y,
y=(110﹣40﹣t)(20+4t)﹣(20+4t)a
化简,得
y=﹣4t2+(260﹣4a)t+1400﹣20a
每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,
∴ ( http: / / www.21cnjy.com )>29.5
解得,a<6,
又∵a>0,
即a的取值范围是:0<a<6.
14.(2018 烟台质检 ( http: / / www.21cnjy.com ))竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= 1.6 .
【分析】设各自抛出后1.1秒时到达相同的最 ( http: / / www.21cnjy.com )大离地高度为h,这个最大高度为h,则小球的高度y=a(t﹣1.1)2+h,根据题意列出方程即可解决问题.
【解答】解:方法一:设各自抛出后1.1秒时到达相同的最大离地高度为h,这个最大高度为h,则小球的高度y=a(t﹣1.1)2+h,
由题意a(t﹣1.1)2+h=a(t﹣1﹣1.1)2+h,
解得t=1.6.
故第一个小球抛出后1.6秒时在空中与第二个小球的离地高度相同.
方法二:结合函数图象可知,两个抛物线的对称轴分别为x=1.1,x=2.1,
t在两条对称轴的中间,故t= ( http: / / www.21cnjy.com )(1.1+2.1)=1.6
故答案为1.6.
15.(2018 泰安质检)某大学生利用业余时间销售一种进价为60元/件的文化衫,前期了解并整理了销售这种文化衫的相关信息如下:21cnjy.com
(1)月销量y(件)与售价x(元)的关系满足:y=﹣2x+400;
(2)工商部门限制销售价x满足:70≤x≤150(计算月利润时不考虑其他成本).给出下列结论:
①这种文化衫的月销量最小为100件;
②这种文化衫的月销量最大为260件;
③销售这种文化衫的月利润最小为2600元;
④销售这种文化衫的月利润最大为9000元.
其中正确的是 ①②③ (把所有正确结论的序号都选上)
【分析】当70≤x≤150时,根据一次函数的 ( http: / / www.21cnjy.com )性质可得y的最大值与最小值即可判断①、②;根据:月利润=(售价﹣成本)×月销量,列出函数关系式并配方,结合x的取值范围可得其最值情况,从而判断③、④.
【解答】解:由题意知,当70≤x≤150时,y=﹣2x+400,
∵﹣2<0,y随x的增大而减小,
∴当x=150时,y取得最小值,最小值为100,故①正确;
当x=70时,y取得最大值,最大值为260,故②正确;
设销售这种文化衫的月利润为W,
则W=(x﹣60)(﹣2x+400)=﹣2(x﹣130)2+9800,
∵70≤x≤150,
∴当x=70时,W取得最小值,最小值为﹣2(70﹣130)2+9800=2600元,故③正确;
当x=130时,W取得最大值,最大值为9800元,故④错误;
故答案为:①②③.
16.(2018 台儿庄月考)某超市销售某种 ( http: / / www.21cnjy.com )玩具,进货价为20元.根据市场调查:在一段时间内,销售单价是30元时,销售量是400件,而销售单价每上涨1元,就会少售出10件玩具,超市要完成不少于300件的销售任务,又要获得最大利润,则销售单价应定为 40 元.
【分析】根据题意分别表示出每件玩具的利润以及销量,进而结合超市要完成不少于300件的销售任务,进而求出x的值.
【解答】解:设销售单价应定为x元,根据题意可得:
利润=(x﹣20)[400﹣10(x﹣30)]
=(x﹣20)(700﹣10x)
=﹣10x2+900x﹣14000
=﹣10(x﹣45)2+6250,
∵超市要完成不少于300件的销售任务,
∴400﹣10(x﹣30)≥300,
解得:x≤40,
即x=40时,销量为300件,此时利润最大为:﹣10(40﹣45)2+6250=6000(元),
故销售单价应定为40元.
故答案为:40.
三.解答题(共20分)
17.(10分)(2017秋 ( http: / / www.21cnjy.com ) 上杭县期中)“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,商场决定采取适当的降价措施.经调查发现,每件该商品每降价1元,商场平均每天可多售出10件.设每件商品降价x元,请回答:
(1)降价后每件商品盈利 (20﹣x) 元,商场日销售量 (100+10x) 件(用含x的代数式表示);【来源:21·世纪·教育·网】
(2)求每件商品降价多少元时,商场日盈利可达到最大?最大日盈利是多少元?
【分析】(1)由题目中的条件即可表示出每件商品的盈利及日销售量;
(2)设每件商品降价x元时,商场日盈利为y元,则可用x表示出y,利用二次函数的性质可求得其最大值.
【解答】解:
(1)∵未降价前每件盈利20元,
∴降价x元后每件商品盈利(20﹣x)元,
∵每件该商品每降价1元,商场平均每天可多售出10件,
∴降价x元后,商场日销售量为(100+10x)件,
故答案为:(20﹣x);(100+10x);
(2)设每件商品降价x元时,商场日盈利为y元,
根据题意得:y=( 20﹣x )( 100+10x )
=﹣10x2+100x+2000
=﹣10( x﹣5 )2+2250 (0≤x≤20),
∴当x=5时,y最大=2250,
答:每件商品降价5元时,商场日盈利可达到最大,最大日盈利是2250元.
18.(10分)(2017 济宁 ( http: / / www.21cnjy.com ))某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=﹣x+60(30≤x≤60).www.21-cn-jy.com
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
【分析】(1)每天的销售利润W=每天的销售量×每件产品的利润;
(2)根据配方法,可得答案;
(3)根据自变量与函数值的对应关系,可得答案.
【解答】解:(1)w=(x﹣30) y=(﹣x+60)(x﹣30)=﹣x2+30x+60x﹣1800=﹣x2+90x﹣1800,【出处:21教育名师】
w与x之间的函数解析式w=﹣x2+90x﹣1800;
(2)根据题意得:w=﹣x2+90x﹣1800=﹣(x﹣45)2+225,
∵﹣1<0,
当x=45时,w有最大值,最大值是225.
(3)当w=200时,﹣x2+90x﹣1800=200,解得x1=40,x2=50,
∵50>48,x2=50不符合题意,舍,
答:该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为40元.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
2.4 二次函数的应用
第二课时检测
(时间45分钟 满分100分)
一.选择题(每小题5分,共50分)
1.(2017 繁昌县模拟)某企业是一家 ( http: / / www.21cnjy.com )专门生产季节性产品的企业,当产品无利润时,企业会自动停产,经过调研预测,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=﹣n2+14n﹣24,则企业停产的月份为( )
A.2月和12月 B.2月至12月 C.1月 D.1月、2月和12月
2.(2017 岱岳区模拟)山东全省201 ( http: / / www.21cnjy.com )6年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )21·世纪*教育网
A.140元 B.150元 C.160元 D.180元
3.(2017 蒙阴县一模)某商人将单价为 ( http: / / www.21cnjy.com )8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高( )21教育名师原创作品
A.8元或10元 B.12元 C.8元 D.10元
4.(2018·滕州鲍沟月 ( http: / / www.21cnjy.com )考)在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )21*cnjy*com
( http: / / www.21cnjy.com )
A.1月份 B.2月份 C.5月份 D.7月份
5.(2018·枣庄周营月考)北国超市 ( http: / / www.21cnjy.com )的小王对该超市苹果的销售进行了统计,某进价为2元/千克的品种的苹果每天的销售量y(千克)和当天的售价x(元/千克)之间满足y=﹣20x+200(3≤x≤5),若要使该品种苹果当天的利润达到最高,则其售价应为[利润=销售量 (售价﹣进价)]( )21*cnjy*com
A.5元 B.4元 C.3.5元 D.3元
6.(2018·枣庄15中质检)如图,2012年伦敦奥运会,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线 ( http: / / www.21cnjy.com )(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为( )米.
( http: / / www.21cnjy.com )
A.10 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
7.(2017秋 全椒县期中)某海 ( http: / / www.21cnjy.com )滨浴场有100个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,…,为了投资少而获利大,每个每天应提高( )
A.4元或6元 B.4元 C.6元 D.8元
8.(2017春 正定县期中)下表 ( http: / / www.21cnjy.com )所列为某商店薄利多销的情况,某商品原价为560元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为500元时,日销量为( )件.
降价(元) 5 10 15 20 25 30 35
日销量(件) 780 810 840 870 900 930 960
A.1200 B.750 C.1110 D.1140
9.(2017春 鼓楼区校级月考)市场调查表明:某种一周内水果的销售率y(销售率= ( http: / / www.21cnjy.com ))与价格倍数x(价格倍数= ( http: / / www.21cnjy.com ))的关系满足函数关系y=﹣ ( http: / / www.21cnjy.com )x+ ( http: / / www.21cnjy.com )(1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
A.120% B.80% C.60% D.40%
10.(2018 枣庄实验质检)一件工艺品的 ( http: / / www.21cnjy.com )进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )
A.3.6 元 B.5 元 C.10 元 D.12 元
二.填空题(每小题5分,共30分)
11.(2017 沈阳)某 ( http: / / www.21cnjy.com )商场购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可销售出400件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,当销售量单价是 元/件,才能在半月内获得最大利润.www-2-1-cnjy-com
12.(2017秋 乳山 ( http: / / www.21cnjy.com )市期中)某商店经销一种成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克,若销售价每涨1元,则月销售量减少10千克.要使月销售利润达到最大,销售单价应定为 元.
13.(2018 滕州月考)某电商销售 ( http: / / www.21cnjy.com )一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 .
14.(2018 烟台质检)竖直上抛的 ( http: / / www.21cnjy.com )小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
15.(2018 泰安质检)某大学生利用业余时间销售一种进价为60元/件的文化衫,前期了解并整理了销售这种文化衫的相关信息如下:
(1)月销量y(件)与售价x(元)的关系满足:y=﹣2x+400;
(2)工商部门限制销售价x满足:70≤x≤150(计算月利润时不考虑其他成本).给出下列结论:
①这种文化衫的月销量最小为100件;
②这种文化衫的月销量最大为260件;
③销售这种文化衫的月利润最小为2600元;
④销售这种文化衫的月利润最大为9000元.
其中正确的是 (把所有正确结论的序号都选上)
16.(2018 台儿庄月考)某超 ( http: / / www.21cnjy.com )市销售某种玩具,进货价为20元.根据市场调查:在一段时间内,销售单价是30元时,销售量是400件,而销售单价每上涨1元,就会少售出10件玩具,超市要完成不少于300件的销售任务,又要获得最大利润,则销售单价应定为 元.
三.解答题(共20分)
17.(10分)(2017秋 上杭县期中 ( http: / / www.21cnjy.com ))“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,商场决定采取适当的降价措施.经调查发现,每件该商品每降价1元,商场平均每天可多售出10件.设每件商品降价x元,请回答:
(1)降价后每件商品盈利 元,商场日销售量 件(用含x的代数式表示);
(2)求每件商品降价多少元时,商场日盈利可达到最大?最大日盈利是多少元?
18.(10分)(2017 济宁)某 ( http: / / www.21cnjy.com )商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=﹣x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
2.4 二次函数的应用
第二课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题5分,共50分)
1.(2017 繁昌县模拟)某企业是一 ( http: / / www.21cnjy.com )家专门生产季节性产品的企业,当产品无利润时,企业会自动停产,经过调研预测,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=﹣n2+14n﹣24,则企业停产的月份为( )
A.2月和12月 B.2月至12月
C.1月 D.1月、2月和12月
【分析】知道利润y和月份n之间函数关系式,求利润y大于0时x的取值.
【解答】解:由题意知,
利润y和月份n之间函数关系式为y=﹣n2+14n﹣24,
∴y=﹣(n﹣2)(n﹣12),
当n=1时,y<0,
当n=2时,y=0,
当n=12时,y=0,
故停产的月份是1月、2月、12月.
故选D.
2.(2017 岱岳区模拟)山 ( http: / / www.21cnjy.com )东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )21教育网
A.140元 B.150元 C.160元 D.180元
【分析】设每张床位提高x个单位,每天收 ( http: / / www.21cnjy.com )入为y元,根据等量关系“每天收入=每张床的费用×每天出租的床位”可求出y与x之间的函数关系式,运用公式求最值即可.
【解答】解:设每张床位提高x个20元,每天收入为y元.
则有y=(100+20x)(100﹣10x)
=﹣200x2+1000x+10000.
当x=﹣ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )=2.5时,可使y有最大值.
又x为整数,则x=2时,y=11200;
x=3时,y=11200;
则为使租出的床位少且租金高,每张床收费=100+3×20=160元,
故选:C.
3.(2017 蒙阴县一模)某商人将单价为 ( http: / / www.21cnjy.com )8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高( )
A.8元或10元 B.12元 C.8元 D.10元
【分析】每件利润为(x﹣8)元,销售量为(100﹣10× ( http: / / www.21cnjy.com )),根据利润=每件利润×销售量,得出销售利润y(元)与售单价x(元)之间的函数关系;再根据函数关系式,利用二次函数的性质求最大利润.
【解答】解:(1)依题意,得y=(x﹣8) (100﹣10× ( http: / / www.21cnjy.com ))=﹣x2+190x﹣1200
=﹣5(x﹣19)2+605,﹣5<0,
∴抛物线开口向下,函数有最大值,
即当x=19时,y的最大值为605,
∵售价为偶数,
∴x为18或20,
当x=18时,y=600,
当x=20时,y=600,
∴x为18或20时y的值相同,
∴商品提高了18﹣10=8(元)或20﹣10=10(元)
故选A.
4.(2018·滕州鲍沟月考 ( http: / / www.21cnjy.com ))在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )21世纪教育网版权所有
( http: / / www.21cnjy.com )
A.1月份 B.2月份 C.5月份 D.7月份
【分析】先根据图中的信息用待定系数法表 ( http: / / www.21cnjy.com )示出每千克售价的一次函数以及每千克成本的二次函数,然后每千克收益=每千克售价﹣每千克成本,得出关于收益和月份的函数关系式,根据函数的性质得出收益的最值以及相应的月份.
【解答】解:设x月份出售时,每千克售价为y1元,每千克成本为y2元.
根据图甲设y1=kx+b,
∴ ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com ),
∴y1=﹣ ( http: / / www.21cnjy.com )x+7.
根据图乙设y2=a(x﹣6)2+1,
∴4=a(3﹣6)2+1,
∴a= ( http: / / www.21cnjy.com ),
∴y2= ( http: / / www.21cnjy.com )(x﹣6)2+1.
∵y=y1﹣y2,
∴y=﹣ ( http: / / www.21cnjy.com )x+7﹣[ ( http: / / www.21cnjy.com )(x﹣6)2+1],
∴y=﹣ ( http: / / www.21cnjy.com )x2+ ( http: / / www.21cnjy.com )x﹣6.
∵y=﹣ ( http: / / www.21cnjy.com )x2+ ( http: / / www.21cnjy.com )x﹣6,
∴y=﹣ ( http: / / www.21cnjy.com )(x﹣5)2+ ( http: / / www.21cnjy.com ).
∴当x=5时,y有最大值,即当5月份出售时,每千克收益最大.
故选C.
5.(2018·枣庄周营月考)北国超市 ( http: / / www.21cnjy.com )的小王对该超市苹果的销售进行了统计,某进价为2元/千克的品种的苹果每天的销售量y(千克)和当天的售价x(元/千克)之间满足y=﹣20x+200(3≤x≤5),若要使该品种苹果当天的利润达到最高,则其售价应为[利润=销售量 (售价﹣进价)]( )2·1·c·n·j·y
A.5元 B.4元 C.3.5元 D.3元
【分析】设销售这种苹果所获得的利润为w, ( http: / / www.21cnjy.com )根据“利润=销售量 (售价﹣进价)“列出函数解析式,并配方成顶点式,利用二次函数的性质可得其最值情况.
【解答】解:设销售这种苹果所获得的利润为w,
则w=(x﹣2)(﹣20x+200)
=﹣20x2+240x﹣400
=﹣20(x﹣6)2+320,
∴当x<6时,w随x的增大而增大,
∵3≤x≤5,
∴当x=5时,w取得最大值,即该品种苹果当天的利润达到最高,
故选:A.
6.(2018·枣庄15中质检)如图,2012年伦敦奥运会,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线 ( http: / / www.21cnjy.com )(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为( )米.
( http: / / www.21cnjy.com )
A.10 B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】首先把抛物线解析式配成顶点式,从而得到抛物线的顶点坐标,进而得到运动员在空中运动的最大高度离水面为多少米.2-1-c-n-j-y
【解答】解:∵ ( http: / / www.21cnjy.com )=﹣ ( http: / / www.21cnjy.com )(x2﹣ ( http: / / www.21cnjy.com )x)=﹣ ( http: / / www.21cnjy.com )(x﹣ ( http: / / www.21cnjy.com ))2+ ( http: / / www.21cnjy.com ),
∴抛物线的顶点坐标是( ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )),
∴运动员在空中运动的最大高度离水面为:10+ ( http: / / www.21cnjy.com )=10 ( http: / / www.21cnjy.com )(米),
故选:D.
7.(2017秋 全椒县期中)某海滨浴场有1 ( http: / / www.21cnjy.com )00个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,…,为了投资少而获利大,每个每天应提高( )
A.4元或6元 B.4元 C.6元 D.8元
【分析】设每个遮阳伞每天应提高x元,每天获得利润为S,每个每天应收费(10+x)元,每天的租出量为(100﹣ ( http: / / www.21cnjy.com )×10=100﹣5x)个,由此列出函数解析式即可解答.
【解答】解:设每个遮阳伞每天应提高x元,每天获得利润为S,由此可得,
S=(10+x)(100﹣ ( http: / / www.21cnjy.com )×10),
整理得S=﹣5x2+50x+1000,
=﹣5(x﹣5)2+1125,
因为每天提高2元,则减少10个,所以当提高4元或6元的时候,获利最大,
又因为为了投资少而获利大,因此应提高6元;
故选C.
8.(2017春 正定县期中)下表所 ( http: / / www.21cnjy.com )列为某商店薄利多销的情况,某商品原价为560元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为500元时,日销量为( )件.【来源:21cnj*y.co*m】
降价(元) 5 10 15 20 25 30 35
日销量(件) 780 810 840 870 900 930 960
A.1200 B.750 C.1110 D.1140
【分析】由表中数据得,每降5元,销售量增加30件,则降60元时,销售量为780加上(60﹣5)×6.【版权所有:21教育】
【解答】解:由表中数据得,每降5元,销售量增加30件,
即每降1元,销售量增加6件,
降560﹣500=60元时,销售量为780+(60﹣5)×6=1110(件).
故选C.
9.(2017春 鼓楼区校级月考)市场调查表明:某种一周内水果的销售率y(销售率= ( http: / / www.21cnjy.com ))与价格倍数x(价格倍数= ( http: / / www.21cnjy.com ))的关系满足函数关系y=﹣ ( http: / / www.21cnjy.com )x+ ( http: / / www.21cnjy.com )(1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
A.120% B.80% C.60% D.40%
【分析】设这种水果的进货价格为a,则售出价格为ax,进货数量为b,则售出数量为by,利润率为p,根据“利润率= ( http: / / www.21cnjy.com )”列出p关于x的函数解析式,利用二次函数的性质求得最值即可.
【解答】解:设这种水果的进货价格为a,则售出价格为ax,进货数量为b,则售出数量为by,利润率为p,
则p= ( http: / / www.21cnjy.com )
=y(x﹣1)
=(﹣ ( http: / / www.21cnjy.com )x+ ( http: / / www.21cnjy.com ))(x﹣1)
=﹣ ( http: / / www.21cnjy.com )x2+ ( http: / / www.21cnjy.com )x﹣ ( http: / / www.21cnjy.com )
=﹣ ( http: / / www.21cnjy.com )(x﹣ ( http: / / www.21cnjy.com ))2+ ( http: / / www.21cnjy.com ),
∵商品售价不得超过进货价格的2倍,
∴x≤2,
∵当x< ( http: / / www.21cnjy.com )时,利润率p随x的增大而减小,
∴当x=2时,p取得最大值,最大值为0.8=80%,
故选:B.
10.(2018 枣庄实验质检)一件工 ( http: / / www.21cnjy.com )艺品的进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )21·cn·jy·com
A.3.6 元 B.5 元 C.10 元 D.12 元
【分析】设每件降价x元,每天获得的利润记 ( http: / / www.21cnjy.com )为W,依据:每天获得的总利润=每件工艺品的利润×每天的销售量,列出函数关系式,配方成顶点式即可得其最值情况.
【解答】解:设每件降价x元,每天获得的利润记为W,
根据题意,W=(135﹣x﹣100)(100+4x)
=﹣4x2+40x+3500
=﹣4(x﹣5)2+3600,
∵﹣4<0,
∴当x=5时,W取得最大值,最大值为3600,
即每件降价5元时,每天获得的利润最大,最大利润为3600元.
故选:B.
二.填空题(每小题5分,共30分)
11.(2017 沈阳)某商场购进 ( http: / / www.21cnjy.com )一批单价为20元的日用商品,如果以单价30元销售,那么半月内可销售出400件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,当销售量单价是 35 元/件,才能在半月内获得最大利润.
【分析】设销售单价为x元,销售利润为y元,求得函数关系式,利用二次函数的性质即可解决问题.
【解答】解:设销售单价为x元,销售利润为y元.
根据题意,得:
y=(x﹣20)[400﹣20(x﹣30)]
=(x﹣20)(1000﹣20x)
=﹣20x2+1400x﹣20000
=﹣20(x﹣35)2+4500,
∵﹣20<0,
∴x=35时,y有最大值,
故答案为35.
12.(2017秋 乳山市期中)某商 ( http: / / www.21cnjy.com )店经销一种成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克,若销售价每涨1元,则月销售量减少10千克.要使月销售利润达到最大,销售单价应定为 70 元.
【分析】设销售单价定为每千克x元,获得 ( http: / / www.21cnjy.com )利润为w元,则可以根据成本,求出每千克的利润,以及按照销售价每涨1元,月销售量就减少10千克,可求出销量.从而得到总利润关系式.
【解答】解:设销售单价定为每千克x元,获得利润为w元,则:
w=(x﹣40)[500﹣(x﹣50)×10],
=(x﹣40)(1000﹣10x),
=﹣10x2+1400x﹣40000,
=﹣10(x﹣70)2+9000,
故当x=70时,利润最大为9000元.
答:要使月销售利润达到最大,销售单价应定为70元.
故答案为70.
13.(2018 滕州月考) ( http: / / www.21cnjy.com )某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 0<a<6 .
【分析】根据题意可以列出相应的不等式,从而可以解答本题.
【解答】解:设未来30天每天获得的利润为y,
y=(110﹣40﹣t)(20+4t)﹣(20+4t)a
化简,得
y=﹣4t2+(260﹣4a)t+1400﹣20a
每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,
∴ ( http: / / www.21cnjy.com )>29.5
解得,a<6,
又∵a>0,
即a的取值范围是:0<a<6.
14.(2018 烟台质检 ( http: / / www.21cnjy.com ))竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= 1.6 .
【分析】设各自抛出后1.1秒时到达相同的最 ( http: / / www.21cnjy.com )大离地高度为h,这个最大高度为h,则小球的高度y=a(t﹣1.1)2+h,根据题意列出方程即可解决问题.
【解答】解:方法一:设各自抛出后1.1秒时到达相同的最大离地高度为h,这个最大高度为h,则小球的高度y=a(t﹣1.1)2+h,
由题意a(t﹣1.1)2+h=a(t﹣1﹣1.1)2+h,
解得t=1.6.
故第一个小球抛出后1.6秒时在空中与第二个小球的离地高度相同.
方法二:结合函数图象可知,两个抛物线的对称轴分别为x=1.1,x=2.1,
t在两条对称轴的中间,故t= ( http: / / www.21cnjy.com )(1.1+2.1)=1.6
故答案为1.6.
15.(2018 泰安质检)某大学生利用业余时间销售一种进价为60元/件的文化衫,前期了解并整理了销售这种文化衫的相关信息如下:21cnjy.com
(1)月销量y(件)与售价x(元)的关系满足:y=﹣2x+400;
(2)工商部门限制销售价x满足:70≤x≤150(计算月利润时不考虑其他成本).给出下列结论:
①这种文化衫的月销量最小为100件;
②这种文化衫的月销量最大为260件;
③销售这种文化衫的月利润最小为2600元;
④销售这种文化衫的月利润最大为9000元.
其中正确的是 ①②③ (把所有正确结论的序号都选上)
【分析】当70≤x≤150时,根据一次函数的 ( http: / / www.21cnjy.com )性质可得y的最大值与最小值即可判断①、②;根据:月利润=(售价﹣成本)×月销量,列出函数关系式并配方,结合x的取值范围可得其最值情况,从而判断③、④.
【解答】解:由题意知,当70≤x≤150时,y=﹣2x+400,
∵﹣2<0,y随x的增大而减小,
∴当x=150时,y取得最小值,最小值为100,故①正确;
当x=70时,y取得最大值,最大值为260,故②正确;
设销售这种文化衫的月利润为W,
则W=(x﹣60)(﹣2x+400)=﹣2(x﹣130)2+9800,
∵70≤x≤150,
∴当x=70时,W取得最小值,最小值为﹣2(70﹣130)2+9800=2600元,故③正确;
当x=130时,W取得最大值,最大值为9800元,故④错误;
故答案为:①②③.
16.(2018 台儿庄月考)某超市销售某种 ( http: / / www.21cnjy.com )玩具,进货价为20元.根据市场调查:在一段时间内,销售单价是30元时,销售量是400件,而销售单价每上涨1元,就会少售出10件玩具,超市要完成不少于300件的销售任务,又要获得最大利润,则销售单价应定为 40 元.
【分析】根据题意分别表示出每件玩具的利润以及销量,进而结合超市要完成不少于300件的销售任务,进而求出x的值.
【解答】解:设销售单价应定为x元,根据题意可得:
利润=(x﹣20)[400﹣10(x﹣30)]
=(x﹣20)(700﹣10x)
=﹣10x2+900x﹣14000
=﹣10(x﹣45)2+6250,
∵超市要完成不少于300件的销售任务,
∴400﹣10(x﹣30)≥300,
解得:x≤40,
即x=40时,销量为300件,此时利润最大为:﹣10(40﹣45)2+6250=6000(元),
故销售单价应定为40元.
故答案为:40.
三.解答题(共20分)
17.(10分)(2017秋 ( http: / / www.21cnjy.com ) 上杭县期中)“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,商场决定采取适当的降价措施.经调查发现,每件该商品每降价1元,商场平均每天可多售出10件.设每件商品降价x元,请回答:
(1)降价后每件商品盈利 (20﹣x) 元,商场日销售量 (100+10x) 件(用含x的代数式表示);【来源:21·世纪·教育·网】
(2)求每件商品降价多少元时,商场日盈利可达到最大?最大日盈利是多少元?
【分析】(1)由题目中的条件即可表示出每件商品的盈利及日销售量;
(2)设每件商品降价x元时,商场日盈利为y元,则可用x表示出y,利用二次函数的性质可求得其最大值.
【解答】解:
(1)∵未降价前每件盈利20元,
∴降价x元后每件商品盈利(20﹣x)元,
∵每件该商品每降价1元,商场平均每天可多售出10件,
∴降价x元后,商场日销售量为(100+10x)件,
故答案为:(20﹣x);(100+10x);
(2)设每件商品降价x元时,商场日盈利为y元,
根据题意得:y=( 20﹣x )( 100+10x )
=﹣10x2+100x+2000
=﹣10( x﹣5 )2+2250 (0≤x≤20),
∴当x=5时,y最大=2250,
答:每件商品降价5元时,商场日盈利可达到最大,最大日盈利是2250元.
18.(10分)(2017 济宁 ( http: / / www.21cnjy.com ))某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=﹣x+60(30≤x≤60).www.21-cn-jy.com
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
【分析】(1)每天的销售利润W=每天的销售量×每件产品的利润;
(2)根据配方法,可得答案;
(3)根据自变量与函数值的对应关系,可得答案.
【解答】解:(1)w=(x﹣30) y=(﹣x+60)(x﹣30)=﹣x2+30x+60x﹣1800=﹣x2+90x﹣1800,【出处:21教育名师】
w与x之间的函数解析式w=﹣x2+90x﹣1800;
(2)根据题意得:w=﹣x2+90x﹣1800=﹣(x﹣45)2+225,
∵﹣1<0,
当x=45时,w有最大值,最大值是225.
(3)当w=200时,﹣x2+90x﹣1800=200,解得x1=40,x2=50,
∵50>48,x2=50不符合题意,舍,
答:该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为40元.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
